
(a)
To calculate: An approximate solution of minimum Hamilton circuit that starts at F, for the given graph and the total weight of the circuit found by using Nearest Neighbor Algorithm.
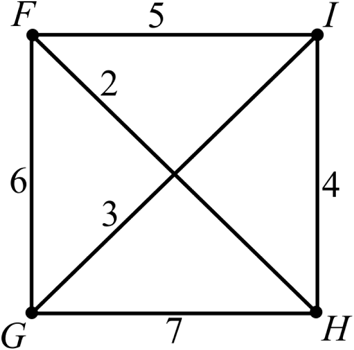
(b)
To calculate: An approximate solution of minimum Hamilton circuit that starts at G, for the given graph and total weight of the circuit found by using Nearest Neighbor Algorithm.

(c)
To calculate: An approximate solution of minimum Hamilton circuit that starts at H, for the given graph and total weight of the circuit found by using Nearest Neighbor Algorithm.

(d)
To calculate: An approximate solution of minimum Hamilton circuit that starts at I, for the given graph and also total weight of the circuit found by using Nearest Neighbor Algorithm.

Want to see the full answer?
Check out a sample textbook solution
Chapter 14 Solutions
Mathematical Ideas with Integrated Review and Worksheets plus NEW MyLab Math with Pearson eText -- Access Card Package (Integrated Review Courses in MyLab Math and MyLab Statistics)
- Consider the network with N = 4 nodes and adjacency matrix A given by A = 0 11 1 1 0 1 1 0000 0000arrow_forward(a) Explain briefly the Dijkstra Algorithm for finding the shortest path of any vertex from a certain starting point vertex, on a Graph (directed or Undirected).arrow_forwardGrid Grove is a neighborhood, with houses organized in m rows of n columns. Houses that are closest to each other are connected by a path (note that this organization follows the definition of a grid graph given in lecture). Assume that m, n > 2. As follows from lecture, Grid Grove has mn houses and 2mn – m -n paths. It is also possible to walk to any house from any other house through some sequence of paths. To save money, the landlords want to get rid of some paths. Calculate D, the maximum number of paths that can be removed from the neighborhood without disconnecting it. Justify your answer. Then describe (informally) which D paths of the neighborhood can be removed (there is more than one such set of D paths).arrow_forward
- How would I use the Extended Euclidean Algorithm to express this gcd as a linear combination? I found the gcd of (14,203) is 7. gcd(14, 203)arrow_forwardGive an example of a bipartite graph on 10 vertices that is (a) 2-regular; (b) 3-regular; (c) 4-regular; (d) 5-regular.arrow_forwardLet P₁ and P₂ be two paths of maximum length in a connected graph G. Prove that P₁ and P2 have a common vertex.arrow_forward
- In Cay({(1, 0), (0, 1)}:Z4 ⊕ Z5), find a sequence of generators thatvisits exactly one vertex twice and all others exactly once and returnsto the starting vertex.arrow_forwardRefer to the accompanying graph. Complete parts (a) through (c) in order. (a) Use the nearest neighbor algorithm starting at each of the vertices in turn to determine an approximate solution to the problem of finding a minimum Hamilton circuit for the graph. In each case, find the total weight of the circuit. Starting at A, the circuit is V and the total weight is Starting at B, the circuit is V and the total weight is Starting at C, the circuit is V and the total weight is Starting at D, the circuit is V and the total weight is Starting at E, the circuit is V and the total weight is (Simplify your answers.) (b) Which of the circuits found in part (a) gives the best solution to the problem of finding a minimum Hamilton circuit for the graph? Select all that apply. O A. The circuit that started at A. O B. The circuit that started at B. Oc. The circuit that started at C. OD. The circuit that started at D. O E. The circuit that started at E. (c) Just by looking carefully at the graph,…arrow_forward2 3) y=-(x– 4)³ + 2(x – 4)³ y Graph showing all algorithm and workarrow_forward
- How long can a path be in the complete bipartite graph k(m,n)?arrow_forwardA chicken farmer wishes to provide electric power to each chicken house on his farm by installing buried electrical power lines. The graph below illustrates the locations of the houses and the distances between them in feet. Use Kruskal's algorithm to determine how the farmer should dig channels in order to minimize the amount of digging. Also determine the minimum total length of channels that must be dug.arrow_forwardDraw a directed graph with as few edges as possible that is strongly-connected, has 8 vertices of which one has in-degree 3, two have out-degree 3, and the rest have smaller in- and out-degrees. Prove that your graph has the minimum number of edges. (Create the drawing in any drawing editor and include it as an image in your answer.)arrow_forward
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

