Mathematical Ideas with Integrated Review and Worksheets plus NEW MyLab Math with Pearson eText -- Access Card Package (Integrated Review Courses in MyLab Math and MyLab Statistics)
1st Edition
ISBN: 9780321977274
Author: Miller, Charles, Heeren, Vern, HORNSBY, John, Christopher
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 14.3, Problem 44E
Nearest Neighbor Algorithm In Exercises 42-44, use the nearest neighbor algorithm starting at each of the indicated vertices to determine an approximate solution to the problem of finding a minimum Hamilton circuit for the graph. In each case, find the total weight of the circuit found.
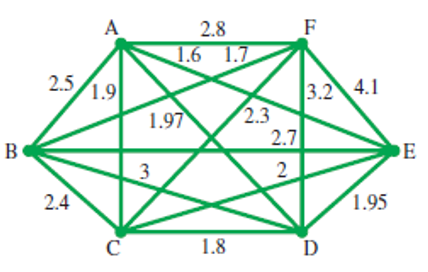
(a) Starting at A
(b) Starting at B
(c) Starting at C
(d) Starting at D
(e) Starting at E
(f) Starting at F
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Given a graph G = (V,E) find the minimum number of edges that will cover every vertex (Edge Cover). Detail and analyze an approximate algorithm to this problem.
Apply Dijkstra's Algorithm to find the shortest path from a to z in the following graph.
Find the shortest path from vertex 'S' to 'T’ by Dijkstra's algorithm for the weighted graph:
3
3
d
1
4
Chapter 14 Solutions
Mathematical Ideas with Integrated Review and Worksheets plus NEW MyLab Math with Pearson eText -- Access Card Package (Integrated Review Courses in MyLab Math and MyLab Statistics)
Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Prob. 4ECh. 14.1 - Prob. 5ECh. 14.1 - Prob. 6ECh. 14.1 - Prob. 7ECh. 14.1 - Prob. 8ECh. 14.1 - Prob. 9ECh. 14.1 - Prob. 10E
Ch. 14.1 - Prob. 11ECh. 14.1 - Prob. 12ECh. 14.1 - Prob. 13ECh. 14.1 - Prob. 14ECh. 14.1 - Prob. 15ECh. 14.1 - Prob. 16ECh. 14.1 - Prob. 17ECh. 14.1 - Prob. 18ECh. 14.1 - Prob. 19ECh. 14.1 - Prob. 20ECh. 14.1 - Prob. 21ECh. 14.1 - Prob. 22ECh. 14.1 - Prob. 23ECh. 14.1 - Prob. 24ECh. 14.1 - Prob. 25ECh. 14.1 - Number of Edges In Exercises 23-26, use the...Ch. 14.1 - Prob. 27ECh. 14.1 - Prob. 28ECh. 14.1 - Prob. 29ECh. 14.1 - Prob. 30ECh. 14.1 - Prob. 31ECh. 14.1 - Prob. 32ECh. 14.1 - Prob. 33ECh. 14.1 - Prob. 34ECh. 14.1 - Prob. 35ECh. 14.1 - Prob. 36ECh. 14.1 - Prob. 37ECh. 14.1 - Prob. 38ECh. 14.1 - Prob. 39ECh. 14.1 - Prob. 40ECh. 14.1 - Prob. 41ECh. 14.1 - Prob. 42ECh. 14.1 - Prob. 43ECh. 14.1 - 44. Chess Competition Students from two schools...Ch. 14.1 - Prob. 45ECh. 14.1 - Prob. 46ECh. 14.1 - Prob. 47ECh. 14.1 - Number of Handshakes There are seven people at a...Ch. 14.1 - Prob. 49ECh. 14.1 - Prob. 50ECh. 14.1 - Prob. 51ECh. 14.1 - 52. Students in the Same Class Mary, Erin, Sue,...Ch. 14.1 - Here is another theorem about graphs: In any...Ch. 14.1 - Draw two nonisomorphic (simple) graphs with 6...Ch. 14.1 - Explain why the two graphs drawn in Exercise 54...Ch. 14.1 - Analyzing a Cube with a Graph Draw a graph whose...Ch. 14.1 - Prob. 57ECh. 14.1 - Prob. 58ECh. 14.1 - Prob. 59ECh. 14.1 - Prob. 60ECh. 14.1 - Prob. 61ECh. 14.1 - Prob. 62ECh. 14.1 - Prob. 63ECh. 14.1 - Prob. 64ECh. 14.1 - Prob. 65ECh. 14.1 - Prob. 66ECh. 14.1 - Prob. 67ECh. 14.1 - Prob. 68ECh. 14.1 - Prob. 69ECh. 14.1 - Prob. 70ECh. 14.1 - 71. Inviting Colleagues to a Gathering Several of...Ch. 14.1 - Prob. 72ECh. 14.1 - Prob. 73ECh. 14.1 - Prob. 74ECh. 14.1 - Prob. 75ECh. 14.1 - Graph Coloring In Exercises 75 and 76, draw a...Ch. 14.1 - Prob. 77ECh. 14.1 - Prob. 78ECh. 14.1 - Prob. 79ECh. 14.1 - Prob. 80ECh. 14.1 - Prob. 81ECh. 14.1 - Prob. 82ECh. 14.1 - The Six Degrees of Kevin Bacon Use the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - 93. Lines from She Walks in Beauty, by Lord...Ch. 14.1 - 94. Lines from Annabel Lee, by Edgar Allan Poe
It...Ch. 14.1 - Poetry Analysis Graphs may be used to clarify the...Ch. 14.1 - 96. Lines from Sailing to Byzantium, by William...Ch. 14.2 - Euler Circuits. In Exercises 1-3, a graph is shown...Ch. 14.2 - Prob. 2ECh. 14.2 - Euler Circuits In Exercises 1-3, a graph is shown...Ch. 14.2 - Prob. 4ECh. 14.2 - Euler's Theorem In Exercises 4-8, use Eulers...Ch. 14.2 - Prob. 6ECh. 14.2 - Euler's Theorem.In Exercises 4-8, use Eider's...Ch. 14.2 - Prob. 8ECh. 14.2 - Euler's Theorem In Exercises 9 and 10, use Eider's...Ch. 14.2 - Prob. 10ECh. 14.2 - Euler's Theorem In Exercises 11-14, use Eider's...Ch. 14.2 - Prob. 12ECh. 14.2 - Euler's Theorem In Exercises 11-14, use Euler's...Ch. 14.2 - Prob. 14ECh. 14.2 - Floor Tilings In Exercises 15-18, different floor...Ch. 14.2 - Prob. 16ECh. 14.2 - Floor Tilings In Exercises 15-18, different floor...Ch. 14.2 - Prob. 18ECh. 14.2 - Prob. 19ECh. 14.2 - Prob. 20ECh. 14.2 - Prob. 21ECh. 14.2 - Prob. 22ECh. 14.2 - Fleury's Algorithm In Exercises 23-25, a graph is...Ch. 14.2 - Prob. 24ECh. 14.2 - Prob. 25ECh. 14.2 - Prob. 26ECh. 14.2 - Fleury's Algorithm In Exercises 26-28\ use...Ch. 14.2 - Prob. 28ECh. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Prob. 32ECh. 14.2 - 33. Parking Pattern The map shows the roads on...Ch. 14.2 - Prob. 34ECh. 14.2 - Floor Plans In Exercises 34-36, the floor plan of...Ch. 14.2 - Prob. 36ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Prob. 38ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Prob. 40ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Floor PlansIn Exercises 41-43, refer to the floor...Ch. 14.2 - Prob. 43ECh. 14.2 - Prob. 44ECh. 14.2 - Prob. 45ECh. 14.2 - Prob. 46ECh. 14.2 - Prob. 47ECh. 14.2 - Prob. 48ECh. 14.2 - Prob. 49ECh. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.3 - Prob. 1ECh. 14.3 - Prob. 2ECh. 14.3 - Euler and Hamilton Circuits In Exercises 3 and 4,...Ch. 14.3 - Euler and Hamilton Circuits In Exercises 3 and 4,...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Prob. 11ECh. 14.3 - Prob. 12ECh. 14.3 - Prob. 13ECh. 14.3 - Decide whether each statement is true or false. If...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - FactorialsIn Exercises 21-24, use a calculator, if...Ch. 14.3 - Factorials In Exercises 21-24, use a calculator,...Ch. 14.3 - Factorials In Exercises 21-24, use a calculator,...Ch. 14.3 - Prob. 24ECh. 14.3 - Hamilton Circuit In Exercises 25-28, determine how...Ch. 14.3 - Prob. 26ECh. 14.3 - Prob. 27ECh. 14.3 - Prob. 28ECh. 14.3 - List all Hamilton circuits in the graph that start...Ch. 14.3 - Prob. 30ECh. 14.3 - Prob. 31ECh. 14.3 - Prob. 32ECh. 14.3 - Prob. 33ECh. 14.3 - Prob. 34ECh. 14.3 - Prob. 35ECh. 14.3 - Prob. 36ECh. 14.3 - Prob. 37ECh. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Prob. 42ECh. 14.3 - Prob. 43ECh. 14.3 - Nearest Neighbor Algorithm In Exercises 42-44, use...Ch. 14.3 - 45. Nearest Neighbor Algorithm Refer to the...Ch. 14.3 - Prob. 46ECh. 14.3 - Prob. 47ECh. 14.3 - Prob. 48ECh. 14.3 - Prob. 49ECh. 14.3 - Hamilton Circuits In Exercises 47-50, find all...Ch. 14.3 - Traveling Salesman Problem The diagram represents...Ch. 14.3 - Prob. 52ECh. 14.3 - The Icosian Game The graph below shows the Icosian...Ch. 14.3 - Prob. 54ECh. 14.3 - Dirac's Theorem Paul A. M. Dirac proved the...Ch. 14.4 - Prob. 1ECh. 14.4 - Prob. 2ECh. 14.4 - Prob. 3ECh. 14.4 - Prob. 4ECh. 14.4 - Prob. 5ECh. 14.4 - Prob. 6ECh. 14.4 - Prob. 7ECh. 14.4 - Prob. 8ECh. 14.4 - Prob. 9ECh. 14.4 - Prob. 10ECh. 14.4 - Prob. 11ECh. 14.4 - Tree or Not a Tree? In Exercises 11-13, determine...Ch. 14.4 - Prob. 13ECh. 14.4 - Prob. 14ECh. 14.4 - Trees and Cut Edges In Exercises 14-17, determine...Ch. 14.4 - Trees and Cut Edges In Exercises 14-17, determine...Ch. 14.4 - Prob. 17ECh. 14.4 - Prob. 18ECh. 14.4 - Prob. 19ECh. 14.4 - Prob. 20ECh. 14.4 - Prob. 21ECh. 14.4 - Prob. 22ECh. 14.4 - Prob. 23ECh. 14.4 - Prob. 24ECh. 14.4 - Prob. 25ECh. 14.4 - Prob. 26ECh. 14.4 - Prob. 27ECh. 14.4 - Prob. 28ECh. 14.4 - Prob. 29ECh. 14.4 - Prob. 30ECh. 14.4 - Prob. 31ECh. 14.4 - Prob. 32ECh. 14.4 - Prob. 33ECh. 14.4 - Town Water Distribution A town council is planning...Ch. 14.4 - Prob. 35ECh. 14.4 - Prob. 36ECh. 14.4 - Prob. 37ECh. 14.4 - Prob. 38ECh. 14.4 - Prob. 39ECh. 14.4 - For Exercise 34
Trees, Edges, and Vertices Work...Ch. 14.4 - 41. Suppose we have a tree with 10 vertices.
(a)...Ch. 14.4 - Prob. 42ECh. 14.4 - Prob. 43ECh. 14.4 - 44. Design of a Garden Maria has 12 vegetable and...Ch. 14.4 - Prob. 45ECh. 14.4 - Prob. 46ECh. 14.4 - Prob. 47ECh. 14.4 - Prob. 48ECh. 14.4 - Prob. 49ECh. 14.4 - Prob. 50ECh. 14.4 - Prob. 51ECh. 14.4 - Prob. 52ECh. 14.4 - Prob. 53ECh. 14.4 - Prob. 54ECh. 14.4 - Prob. 55ECh. 14.4 - Vertex/Edge Relationship In this exercise, we...Ch. 14 - Basic Concepts In Exercises 1-5, refer to the...Ch. 14 - Basic Concepts In Exercises 1-5, refer to the...Ch. 14 - Prob. 3TCh. 14 - Prob. 4TCh. 14 - Prob. 5TCh. 14 - Prob. 6TCh. 14 - Prob. 7TCh. 14 - Prob. 8TCh. 14 - Planning for Dinner Julia is planning to invite...Ch. 14 - Prob. 10TCh. 14 - Prob. 11TCh. 14 - Prob. 12TCh. 14 - Prob. 13TCh. 14 - Scheduling Exams A teacher at a high school must...Ch. 14 - Prob. 15TCh. 14 - Prob. 16TCh. 14 - Prob. 17TCh. 14 - Prob. 18TCh. 14 - Prob. 19TCh. 14 - Prob. 20TCh. 14 - Prob. 21TCh. 14 - Prob. 22TCh. 14 - Prob. 23TCh. 14 - Prob. 24TCh. 14 - Prob. 25TCh. 14 - 26. Nonisomorphic Trees Draw three nonisomorphic...Ch. 14 - Prob. 27TCh. 14 - Prob. 28TCh. 14 - Prob. 29TCh. 14 - Prob. 30TCh. 14 - Prob. 31TCh. 14 - Prob. 32T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Grid Grove is a neighborhood, with houses organized in m rows of n columns. Houses that are closest to each other are connected by a path (note that this organization follows the definition of a grid graph given in lecture). Assume that m, n > 2. As follows from lecture, Grid Grove has mn houses and 2mn – m -n paths. It is also possible to walk to any house from any other house through some sequence of paths. To save money, the landlords want to get rid of some paths. Calculate D, the maximum number of paths that can be removed from the neighborhood without disconnecting it. Justify your answer. Then describe (informally) which D paths of the neighborhood can be removed (there is more than one such set of D paths).arrow_forwardHow would I use the Extended Euclidean Algorithm to express this gcd as a linear combination? I found the gcd of (14,203) is 7. gcd(14, 203)arrow_forwardDraw a directed graph with as few edges as possible that is strongly-connected, has 8 vertices of which one has in-degree 3, two have out-degree 3, and the rest have smaller in- and out-degrees. Prove that your graph has the minimum number of edges. (Create the drawing in any drawing editor and include it as an image in your answer.)arrow_forward
- Refer to the accompanying graph. Complete parts (a) through (c) in order. (a) Use the nearest neighbor algorithm starting at each of the vertices in turn to determine an approximate solution to the problem of finding a minimum Hamilton circuit for the graph. In each case, find the total weight of the circuit. Starting at A, the circuit is V and the total weight is Starting at B, the circuit is V and the total weight is Starting at C, the circuit is V and the total weight is Starting at D, the circuit is V and the total weight is Starting at E, the circuit is V and the total weight is (Simplify your answers.) (b) Which of the circuits found in part (a) gives the best solution to the problem of finding a minimum Hamilton circuit for the graph? Select all that apply. O A. The circuit that started at A. O B. The circuit that started at B. Oc. The circuit that started at C. OD. The circuit that started at D. O E. The circuit that started at E. (c) Just by looking carefully at the graph,…arrow_forwardGive an example of a bipartite graph on 10 vertices that is (a) 2-regular; (b) 3-regular; (c) 4-regular; (d) 5-regular.arrow_forwardA chicken farmer wishes to provide electric power to each chicken house on his farm by installing buried electrical power lines. The graph below illustrates the locations of the houses and the distances between them in feet. Use Kruskal's algorithm to determine how the farmer should dig channels in order to minimize the amount of digging. Also determine the minimum total length of channels that must be dug.arrow_forward
- C D 21 20 15 B Apply the nearest neighbor algorithm to the graph above starting at vertex A. Give your answer as a list of vertices, starting and ending at vertex A. Example: ABCDAarrow_forwardUsing Dijkstra's shortest path algorithm calculate the shortest path from Node X through to Node Z in the diagram below. You should clearly show each step of the algorithm. Find the weights using code 20194986 in the following order: abcdefgh. (e.g., if your code was 12345678, then a=1, b=2, c=3, ..., g=7, h=8). Afterwards, calculate the shortest path from Node X to Node Z using Dijkstra's shortest path algorithm.arrow_forwardHow long can a path be in the complete bipartite graph k(m,n)?arrow_forward
- Use the Nearest Neighbor Algorithm starting at vertex A to estimate the optimal Hamiltonian circuit. The Hamiltonian circuit which gives an estimate to the optimal solution is. The estimate for the optimal solution given by the Hamiltonian circuit is. IMMAGE ATTACHEDarrow_forwardII. Use Euclidean Algorithm to obtain x and y satisfying the equation of (50 364, 26 601) = 50 364x + 26 601y. (8 points)arrow_forward1a. Prove: every tree with n ≥ 2 vertices has at least 2 leaves. (3 pt) 1b. Let T be a tree. Prove: if all vertices have degree either 1 or at least 4, then T has at least 2(n + 1)/3 leaves. (4 pt)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Orthogonality in Inner Product Spaces; Author: Study Force;https://www.youtube.com/watch?v=RzIx_rRo9m0;License: Standard YouTube License, CC-BY
Abstract Algebra: The definition of a Group; Author: Socratica;https://www.youtube.com/watch?v=QudbrUcVPxk;License: Standard Youtube License