Chapter 14.2, Problem 37E

Exercises 37-44 are based on the following theorem:

If a graph has an Euler path that begins and ends at different vertices, then these two vertices are the only vertices with odd degree. (All the rest have even degree.)

If exactly two vertices in a connected graph have odd degree, then the graph has an Euler path beginning at one of these vertices and ending at the other.

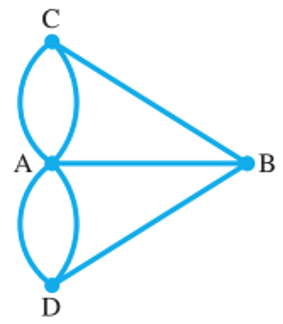
In Exercises 37-40, determine whether the graph has an Euler path that begins and ends at different vertices. Justify your answer. If the graph has such a path, say at which vertices the path must begin and end.