Mathematical Ideas with Integrated Review and Worksheets plus NEW MyLab Math with Pearson eText -- Access Card Package (Integrated Review Courses in MyLab Math and MyLab Statistics)
1st Edition
ISBN: 9780321977274
Author: Miller, Charles, Heeren, Vern, HORNSBY, John, Christopher
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 14.3, Problem 10E
Hamilton Circuits In Exercises 5-10, determine whether the graph has a Hamilton circuit. If so, find one. (There may be many different correct answers.)
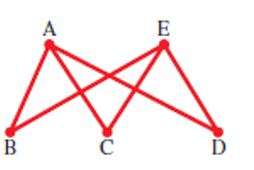
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Discrete Math
Discrete Math
A map of a park is shown with bridges connecting islands in a river to the banks.
d. Represent the map as a graph.
e. Is it possible to take a walk that crosses each bridge once and return to the starting point
without crossing any bridge twice? If not, can you do it if you do not end at the starting
point?
Chapter 14 Solutions
Mathematical Ideas with Integrated Review and Worksheets plus NEW MyLab Math with Pearson eText -- Access Card Package (Integrated Review Courses in MyLab Math and MyLab Statistics)
Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Prob. 4ECh. 14.1 - Prob. 5ECh. 14.1 - Prob. 6ECh. 14.1 - Prob. 7ECh. 14.1 - Prob. 8ECh. 14.1 - Prob. 9ECh. 14.1 - Prob. 10E
Ch. 14.1 - Prob. 11ECh. 14.1 - Prob. 12ECh. 14.1 - Prob. 13ECh. 14.1 - Prob. 14ECh. 14.1 - Prob. 15ECh. 14.1 - Prob. 16ECh. 14.1 - Prob. 17ECh. 14.1 - Prob. 18ECh. 14.1 - Prob. 19ECh. 14.1 - Prob. 20ECh. 14.1 - Prob. 21ECh. 14.1 - Prob. 22ECh. 14.1 - Prob. 23ECh. 14.1 - Prob. 24ECh. 14.1 - Prob. 25ECh. 14.1 - Number of Edges In Exercises 23-26, use the...Ch. 14.1 - Prob. 27ECh. 14.1 - Prob. 28ECh. 14.1 - Prob. 29ECh. 14.1 - Prob. 30ECh. 14.1 - Prob. 31ECh. 14.1 - Prob. 32ECh. 14.1 - Prob. 33ECh. 14.1 - Prob. 34ECh. 14.1 - Prob. 35ECh. 14.1 - Prob. 36ECh. 14.1 - Prob. 37ECh. 14.1 - Prob. 38ECh. 14.1 - Prob. 39ECh. 14.1 - Prob. 40ECh. 14.1 - Prob. 41ECh. 14.1 - Prob. 42ECh. 14.1 - Prob. 43ECh. 14.1 - 44. Chess Competition Students from two schools...Ch. 14.1 - Prob. 45ECh. 14.1 - Prob. 46ECh. 14.1 - Prob. 47ECh. 14.1 - Number of Handshakes There are seven people at a...Ch. 14.1 - Prob. 49ECh. 14.1 - Prob. 50ECh. 14.1 - Prob. 51ECh. 14.1 - 52. Students in the Same Class Mary, Erin, Sue,...Ch. 14.1 - Here is another theorem about graphs: In any...Ch. 14.1 - Draw two nonisomorphic (simple) graphs with 6...Ch. 14.1 - Explain why the two graphs drawn in Exercise 54...Ch. 14.1 - Analyzing a Cube with a Graph Draw a graph whose...Ch. 14.1 - Prob. 57ECh. 14.1 - Prob. 58ECh. 14.1 - Prob. 59ECh. 14.1 - Prob. 60ECh. 14.1 - Prob. 61ECh. 14.1 - Prob. 62ECh. 14.1 - Prob. 63ECh. 14.1 - Prob. 64ECh. 14.1 - Prob. 65ECh. 14.1 - Prob. 66ECh. 14.1 - Prob. 67ECh. 14.1 - Prob. 68ECh. 14.1 - Prob. 69ECh. 14.1 - Prob. 70ECh. 14.1 - 71. Inviting Colleagues to a Gathering Several of...Ch. 14.1 - Prob. 72ECh. 14.1 - Prob. 73ECh. 14.1 - Prob. 74ECh. 14.1 - Prob. 75ECh. 14.1 - Graph Coloring In Exercises 75 and 76, draw a...Ch. 14.1 - Prob. 77ECh. 14.1 - Prob. 78ECh. 14.1 - Prob. 79ECh. 14.1 - Prob. 80ECh. 14.1 - Prob. 81ECh. 14.1 - Prob. 82ECh. 14.1 - The Six Degrees of Kevin Bacon Use the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - 93. Lines from She Walks in Beauty, by Lord...Ch. 14.1 - 94. Lines from Annabel Lee, by Edgar Allan Poe
It...Ch. 14.1 - Poetry Analysis Graphs may be used to clarify the...Ch. 14.1 - 96. Lines from Sailing to Byzantium, by William...Ch. 14.2 - Euler Circuits. In Exercises 1-3, a graph is shown...Ch. 14.2 - Prob. 2ECh. 14.2 - Euler Circuits In Exercises 1-3, a graph is shown...Ch. 14.2 - Prob. 4ECh. 14.2 - Euler's Theorem In Exercises 4-8, use Eulers...Ch. 14.2 - Prob. 6ECh. 14.2 - Euler's Theorem.In Exercises 4-8, use Eider's...Ch. 14.2 - Prob. 8ECh. 14.2 - Euler's Theorem In Exercises 9 and 10, use Eider's...Ch. 14.2 - Prob. 10ECh. 14.2 - Euler's Theorem In Exercises 11-14, use Eider's...Ch. 14.2 - Prob. 12ECh. 14.2 - Euler's Theorem In Exercises 11-14, use Euler's...Ch. 14.2 - Prob. 14ECh. 14.2 - Floor Tilings In Exercises 15-18, different floor...Ch. 14.2 - Prob. 16ECh. 14.2 - Floor Tilings In Exercises 15-18, different floor...Ch. 14.2 - Prob. 18ECh. 14.2 - Prob. 19ECh. 14.2 - Prob. 20ECh. 14.2 - Prob. 21ECh. 14.2 - Prob. 22ECh. 14.2 - Fleury's Algorithm In Exercises 23-25, a graph is...Ch. 14.2 - Prob. 24ECh. 14.2 - Prob. 25ECh. 14.2 - Prob. 26ECh. 14.2 - Fleury's Algorithm In Exercises 26-28\ use...Ch. 14.2 - Prob. 28ECh. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Prob. 32ECh. 14.2 - 33. Parking Pattern The map shows the roads on...Ch. 14.2 - Prob. 34ECh. 14.2 - Floor Plans In Exercises 34-36, the floor plan of...Ch. 14.2 - Prob. 36ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Prob. 38ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Prob. 40ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Floor PlansIn Exercises 41-43, refer to the floor...Ch. 14.2 - Prob. 43ECh. 14.2 - Prob. 44ECh. 14.2 - Prob. 45ECh. 14.2 - Prob. 46ECh. 14.2 - Prob. 47ECh. 14.2 - Prob. 48ECh. 14.2 - Prob. 49ECh. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.3 - Prob. 1ECh. 14.3 - Prob. 2ECh. 14.3 - Euler and Hamilton Circuits In Exercises 3 and 4,...Ch. 14.3 - Euler and Hamilton Circuits In Exercises 3 and 4,...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Prob. 11ECh. 14.3 - Prob. 12ECh. 14.3 - Prob. 13ECh. 14.3 - Decide whether each statement is true or false. If...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - FactorialsIn Exercises 21-24, use a calculator, if...Ch. 14.3 - Factorials In Exercises 21-24, use a calculator,...Ch. 14.3 - Factorials In Exercises 21-24, use a calculator,...Ch. 14.3 - Prob. 24ECh. 14.3 - Hamilton Circuit In Exercises 25-28, determine how...Ch. 14.3 - Prob. 26ECh. 14.3 - Prob. 27ECh. 14.3 - Prob. 28ECh. 14.3 - List all Hamilton circuits in the graph that start...Ch. 14.3 - Prob. 30ECh. 14.3 - Prob. 31ECh. 14.3 - Prob. 32ECh. 14.3 - Prob. 33ECh. 14.3 - Prob. 34ECh. 14.3 - Prob. 35ECh. 14.3 - Prob. 36ECh. 14.3 - Prob. 37ECh. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Prob. 42ECh. 14.3 - Prob. 43ECh. 14.3 - Nearest Neighbor Algorithm In Exercises 42-44, use...Ch. 14.3 - 45. Nearest Neighbor Algorithm Refer to the...Ch. 14.3 - Prob. 46ECh. 14.3 - Prob. 47ECh. 14.3 - Prob. 48ECh. 14.3 - Prob. 49ECh. 14.3 - Hamilton Circuits In Exercises 47-50, find all...Ch. 14.3 - Traveling Salesman Problem The diagram represents...Ch. 14.3 - Prob. 52ECh. 14.3 - The Icosian Game The graph below shows the Icosian...Ch. 14.3 - Prob. 54ECh. 14.3 - Dirac's Theorem Paul A. M. Dirac proved the...Ch. 14.4 - Prob. 1ECh. 14.4 - Prob. 2ECh. 14.4 - Prob. 3ECh. 14.4 - Prob. 4ECh. 14.4 - Prob. 5ECh. 14.4 - Prob. 6ECh. 14.4 - Prob. 7ECh. 14.4 - Prob. 8ECh. 14.4 - Prob. 9ECh. 14.4 - Prob. 10ECh. 14.4 - Prob. 11ECh. 14.4 - Tree or Not a Tree? In Exercises 11-13, determine...Ch. 14.4 - Prob. 13ECh. 14.4 - Prob. 14ECh. 14.4 - Trees and Cut Edges In Exercises 14-17, determine...Ch. 14.4 - Trees and Cut Edges In Exercises 14-17, determine...Ch. 14.4 - Prob. 17ECh. 14.4 - Prob. 18ECh. 14.4 - Prob. 19ECh. 14.4 - Prob. 20ECh. 14.4 - Prob. 21ECh. 14.4 - Prob. 22ECh. 14.4 - Prob. 23ECh. 14.4 - Prob. 24ECh. 14.4 - Prob. 25ECh. 14.4 - Prob. 26ECh. 14.4 - Prob. 27ECh. 14.4 - Prob. 28ECh. 14.4 - Prob. 29ECh. 14.4 - Prob. 30ECh. 14.4 - Prob. 31ECh. 14.4 - Prob. 32ECh. 14.4 - Prob. 33ECh. 14.4 - Town Water Distribution A town council is planning...Ch. 14.4 - Prob. 35ECh. 14.4 - Prob. 36ECh. 14.4 - Prob. 37ECh. 14.4 - Prob. 38ECh. 14.4 - Prob. 39ECh. 14.4 - For Exercise 34
Trees, Edges, and Vertices Work...Ch. 14.4 - 41. Suppose we have a tree with 10 vertices.
(a)...Ch. 14.4 - Prob. 42ECh. 14.4 - Prob. 43ECh. 14.4 - 44. Design of a Garden Maria has 12 vegetable and...Ch. 14.4 - Prob. 45ECh. 14.4 - Prob. 46ECh. 14.4 - Prob. 47ECh. 14.4 - Prob. 48ECh. 14.4 - Prob. 49ECh. 14.4 - Prob. 50ECh. 14.4 - Prob. 51ECh. 14.4 - Prob. 52ECh. 14.4 - Prob. 53ECh. 14.4 - Prob. 54ECh. 14.4 - Prob. 55ECh. 14.4 - Vertex/Edge Relationship In this exercise, we...Ch. 14 - Basic Concepts In Exercises 1-5, refer to the...Ch. 14 - Basic Concepts In Exercises 1-5, refer to the...Ch. 14 - Prob. 3TCh. 14 - Prob. 4TCh. 14 - Prob. 5TCh. 14 - Prob. 6TCh. 14 - Prob. 7TCh. 14 - Prob. 8TCh. 14 - Planning for Dinner Julia is planning to invite...Ch. 14 - Prob. 10TCh. 14 - Prob. 11TCh. 14 - Prob. 12TCh. 14 - Prob. 13TCh. 14 - Scheduling Exams A teacher at a high school must...Ch. 14 - Prob. 15TCh. 14 - Prob. 16TCh. 14 - Prob. 17TCh. 14 - Prob. 18TCh. 14 - Prob. 19TCh. 14 - Prob. 20TCh. 14 - Prob. 21TCh. 14 - Prob. 22TCh. 14 - Prob. 23TCh. 14 - Prob. 24TCh. 14 - Prob. 25TCh. 14 - 26. Nonisomorphic Trees Draw three nonisomorphic...Ch. 14 - Prob. 27TCh. 14 - Prob. 28TCh. 14 - Prob. 29TCh. 14 - Prob. 30TCh. 14 - Prob. 31TCh. 14 - Prob. 32T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 31 Part 1 of 2 NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Consider the graph. a b □ Identify the true statement about the graph shown. (You must provide an answer before moving to the next part.) Multiple Choice It has both multiple edges and loops. It has no multiple edges and no loops. It has no multiple edges, but it has loops. It has multiple edges, but it has no loops.arrow_forwardDISCRETE MATHEMATICS Part II. COMPUTATION. A graph contains 21 edges, 3 vertices of degree 4 and all other vertices of degree 2. Find total number of vertices. A simple graph contains 35 edges, four vertices of degree 5, five vertices of degree 4 and four vertices of degree 3. Find the number of vertices with degree 2.arrow_forwardDiscrete Math:arrow_forward
- A map of a park is shown with bridges connecting islands in a river to the banks. (a) Represent the map as a graph. See these figures for an example. (b) Is it possible to take a walk that crosses each bridge once and return to the starting point without crossing any bridge twice? If not, can you do it if you do not end at the starting point? Explain how you know. Oit is not possible, returning to the starting point. However, it is possible if you do not return to the starting point, because exactly two vertices are of even degree. Olt is not possible, nor is it possible even if you do not return to the starting point. Every vertex of the graph has an odd degree. Oit is possible. Every vertex of the graph has an even degree. Olt is not possible, returning to the starting point. However, it is possible if you do not return to the starting point, because exactly two vertices are of odd degree. Oit is possible. Every vertex of the graph has an odd degree.arrow_forwardDiscrete math problemConstruct a directed network whose vertices represent the numbers:11,12,13,15,17and whose weights tell how much you must add to get from one vertex to another. Include only edges of positive weight.arrow_forwardIf G is a connected graph with no bridges, how many vertices of degree 1 can G have? Explain your answer. In chapter 5 excursions in modern mathematicsarrow_forward
- Essentials of DISCRETE MATHEMATICS Section 2.6 - Graph Theory First write a definition of a subgraph and then solve #29arrow_forwardUse Euler's theorem to determine whether the graph has an Euler path (but not an Euler circuit), Euler circuit, or neither. A C D F E Explain your answer?arrow_forwardConsider the tree diagram. Path number 1 C B1 C2 3 B2. 4 C2 C B3 C2 C3 7 Find P(C|B2) · P(B2). (Enter your answer as a fraction.) Read It Need Help? 2. +1n1/4 /4 /2arrow_forward
- *discrete mathematics Please do not reject I am in desperate need of help. Please explain with clear steps thank you!arrow_forwardOther Math A simple graph G has 10 vertices and 38 edges. (b) Prove that G must have a Hamilton circuit. (Hint: You will need Ore’s Theorem.)arrow_forwardWhat are the strongly connected components of the digraph below? Your answer should consist of a list of strongly connected components where each component is represented as a set of vertices.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Orthogonality in Inner Product Spaces; Author: Study Force;https://www.youtube.com/watch?v=RzIx_rRo9m0;License: Standard YouTube License, CC-BY
Abstract Algebra: The definition of a Group; Author: Socratica;https://www.youtube.com/watch?v=QudbrUcVPxk;License: Standard Youtube License