Chapter 14, Problem 9PQ

The keystone of an arch is the stone at the top (Fig. P14.9). It is supported by forces from its two neighbors, blocks A and B. Each block has mass m and approximate length L. What can you conclude about the force exerted by each block, ${\stackrel{\to }{F}}_A$ and ${\stackrel{\to }{F}}_B$, for the keystone to remain in static equilibrium? That is, show that the equilibrium conditions are satisfied by the components of the forces F_Ax, F_Ay, F_Bx, and F_By. Assume the arch is symmetric.

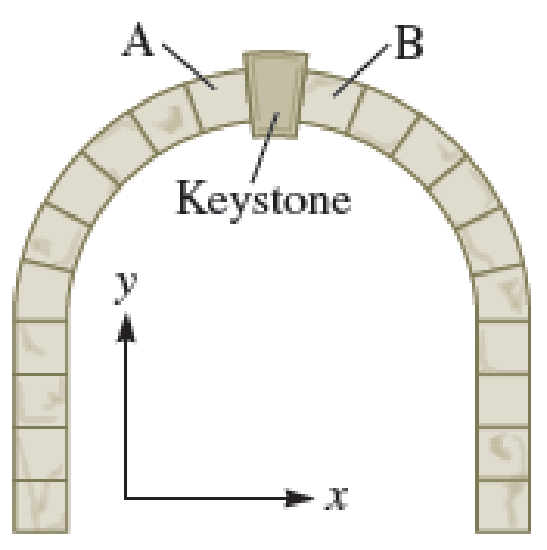
FIGURE P14.9

To determine

To show that the equilibrium conditions are satisfied by the components of the forces $F_{Ax}$, $F_{Ay}$ , $F_{Bx}$ and $F_{By}$ by assuming that arch is symmetric.

Answer to Problem 9PQ

It is showed that the equilibrium conditions are satisfied by the components of the forces $F_{Ax}$, $F_{Ay}$ , $F_{Bx}$ and $F_{By}$.

Explanation of Solution

A body remains in static equilibrium if net force and torque is equal to zero.

The forces acting on the keystone are force from block A , force from block B and force of gravity, which points downward.

Write the expression for the net force acting on the keystone by block A.

  ${\overrightarrow{\text{F}}}_A=F_{Ax}\widehat{\text{i}}\text{+}{F}_{Ay}\widehat{\text{j}}$                                                                                                        (I)

Here, ${\overrightarrow{\text{F}}}_A$ is the net force acting on the keystone by block A, $F_{Ax}$ is the $x$ component of ${\overrightarrow{\text{F}}}_A$, $F_{Ay}$ is the $y$ component of ${\overrightarrow{\text{F}}}_A$ , $\widehat{\text{i}}$ is the unit vector along $x$ direction and $\widehat{\text{j}}$ is unit vector along $y$ direction.

Write the expression for the net force acting on the keystone by block B.

  ${\overrightarrow{\text{F}}}_B=F_{Bx}\widehat{\text{i}}\text{+}{F}_{By}\widehat{\text{j}}$                                                                                                       (II)

Here, ${\overrightarrow{\text{F}}}_B$ is the net force acting on the keystone by block B, $F_{Bx}$ is the $x$ component of ${\overrightarrow{\text{F}}}_B$, $F_{By}$ is the $y$ component of ${\overrightarrow{\text{F}}}_B$ ,

Write the expression for the force of gravity on Keystone.

  ${\overrightarrow{\text{F}}}_g=-mg\widehat{\text{j}}$                                                                                                              (III)

Here, ${\overrightarrow{\text{F}}}_g$ is the force of gravity on Keystone, $m$ is the mass of the Keystone and $g$ is the acceleration due to gravity.

It is given that Keystone is in static equilibrium.

Write the equilibrium condition for the forces along $x$ direction.

  ${\displaystyle \sum F_x}=0$                                                                                                                (IV)

Here, ${\displaystyle \sum F_x}$ is the net force along $x$ direction.

Expand above equation using components of forces along $x$ direction.

  $F_{Ax}+F_{Bx}=0$                                                                                                             (V)

Rearrange above equation to get $F_{Ax}$ .

  $F_{Ax}=-F_{Bx}$                                                                                                               (VI)

Write the equilibrium condition for the forces along $y$ direction.

  ${\displaystyle \sum F_y}=0$                                                                                                              (VII)

Here, ${\displaystyle \sum F_y}$ is the net force along $y$ direction.

Expand above equation using components of forces along $y$ direction.

  $F_{Ay}+F_{By}-mg=0$                                                                                               (VIII)

Assume that arch is symmetric.

  $F_{Ay}=F_{By}$                                                                                                                 (IX)

Substitute $F_{Ay}$ for $F_{By}$ in equation (VIII) to get $F_{Ay}$.

  $\begin{array}{c}{F}_{Ay}+F_{Ay}-mg=0\\ 2F_{Ay}-mg=0\\ F_{Ay}=\frac{mg}{2}\end{array}$                                                                                               (X)

Put the above equation in equation (IX).

  $F_{Ay}=F_{By}=\frac{mg}{2}$                                                                                                       (XI)

Substitute $\frac{mg}{2}$ for $F_{Ay}$ in equation (I) to get ${\overrightarrow{\text{F}}}_A$.

  ${\overrightarrow{\text{F}}}_A=F_{Ax}\widehat{\text{i}}\text{+}\frac{mg}{2}\widehat{\text{j}}$                                                                                                  (XII)

Substitute $\frac{mg}{2}$ for $F_{By}$ in equation (II) to get ${\overrightarrow{\text{F}}}_B$.

  ${\overrightarrow{\text{F}}}_B=F_{Bx}\widehat{\text{i}}\text{+}\frac{mg}{2}\widehat{\text{j}}$                                                                                                 (XIII)

Write the expression for the torque acting on the keystone due to force ${\overrightarrow{\text{F}}}_A$.

  ${\overrightarrow{\tau }}_A={\overrightarrow{\text{r}}}_A\times {\overrightarrow{\text{F}}}_A$                                                                                                          (XIV)

Here, ${\overrightarrow{\tau }}_A$ is the torque about center of Keystone due to force ${\overrightarrow{\text{F}}}_A$ and ${\overrightarrow{\text{r}}}_A$ is the position vector of center of block A from center of Keystone.

It is given that length of each block is $L$ .

Write the expression for ${\overrightarrow{\text{r}}}_A$.

  ${\overrightarrow{\text{r}}}_A=-\frac{L}{2}\widehat{\text{i}}$                                                                                                              (XV)

Substitute $-\frac{L}{2}\widehat{\text{i}}$ for ${\overrightarrow{\text{r}}}_A$ and $F_{Ax}\widehat{\text{i}}\text{+}\frac{mg}{2}\widehat{\text{j}}$ for ${\overrightarrow{\text{F}}}_A$ in equation (XIV) to get ${\overrightarrow{\tau }}_A$ .

  $\begin{array}{c}{\overrightarrow{\tau }}_A=-\frac{L}{2}\widehat{\text{i}}\times \left(F_{Ax}\widehat{\text{i}}\text{+}\frac{mg}{2}\widehat{\text{j}}\right)\\ =-\frac{L}{2}\widehat{\text{i}}\times F_{Ax}\widehat{\text{i}}+-\frac{L}{2}\widehat{\text{i}}\times \frac{mg}{2}\widehat{\text{j}}\\ \text{=}-\frac{L{F}_{Ax}}{2}\left(\widehat{\text{i}}\times \widehat{\text{i}}\right)-\frac{mgL}{4}\left(\widehat{\text{i}}\times \widehat{\text{j}}\right)\end{array}$

Use expressions $\widehat{\text{i}}\times \widehat{\text{i}}=0$ and $\widehat{\text{i}}\times \widehat{\text{j}}=\widehat{\text{k}}$ in above equation to get ${\overrightarrow{\tau }}_A$.

  $\begin{array}{c}{\overrightarrow{\tau }}_A=0-\frac{mgL}{4}\widehat{\text{k}}\\ \text{=}-\frac{mgL}{4}\widehat{\text{k}}\end{array}$

Write the expression for the torque acting on the keystone due to force ${\overrightarrow{\text{F}}}_B$.

  ${\overrightarrow{\tau }}_B={\overrightarrow{\text{r}}}_B\times {\overrightarrow{\text{F}}}_B$                                                                                                          (XVI)

Here, ${\overrightarrow{\tau }}_B$ is the torque about center of Keystone due to force ${\overrightarrow{\text{F}}}_B$ and ${\overrightarrow{\text{r}}}_B$ is the position vector of center of block B from center of Keystone.

Write the expression for ${\overrightarrow{\text{r}}}_B$.

  ${\overrightarrow{\text{r}}}_B=\frac{L}{2}\widehat{\text{i}}$                                                                                                              (XV)

Substitute $\frac{L}{2}\widehat{\text{i}}$ for ${\overrightarrow{\text{r}}}_B$ and $F_{Bx}\widehat{\text{i}}\text{+}\frac{mg}{2}\widehat{\text{j}}$ for ${\overrightarrow{\text{F}}}_B$ in equation (XVI) to get ${\overrightarrow{\tau }}_B$ .

  $\begin{array}{c}{\overrightarrow{\tau }}_B=\frac{L}{2}\widehat{\text{i}}\times \left(F_{Bx}\widehat{\text{i}}\text{+}\frac{mg}{2}\widehat{\text{j}}\right)\\ =\frac{L}{2}\widehat{\text{i}}\times F_{Bx}\widehat{\text{i}}+\frac{L}{2}\widehat{\text{i}}\times \frac{mg}{2}\widehat{\text{j}}\\ \text{=}\frac{L{F}_{Bx}}{2}\left(\widehat{\text{i}}\times \widehat{\text{i}}\right)+\frac{mgL}{4}\left(\widehat{\text{i}}\times \widehat{\text{j}}\right)\end{array}$

Use expressions $\widehat{\text{i}}\times \widehat{\text{i}}=0$ and $\widehat{\text{i}}\times \widehat{\text{j}}=\widehat{\text{k}}$ in above equation to get ${\overrightarrow{\tau }}_B$.

  $\begin{array}{c}{\overrightarrow{\tau }}_B=0+\frac{mgL}{4}\widehat{\text{k}}\\ \text{=}\frac{mgL}{4}\widehat{\text{k}}\end{array}$

Thus, torque ${\overrightarrow{\tau }}_A$ is in $-z$ direction and torque ${\overrightarrow{\tau }}_B$ is in $+z$ direction. Since ${\overrightarrow{\tau }}_A$ and ${\overrightarrow{\tau }}_B$ are same in magnitude and opposite in direction, they cancel each other to give net torque equal to zero.

Conclusion:

From above calculations it is clear that, net force and net torque are zero if $F_{Ay}=F_{By}=\frac{mg}{2}$ and $F_{Ax}=-F_{Bx}$. This is true in the case of symmetric arch.

Each of the neighboring block supports half the weight of the keystone and the forces in the $x$ direction are equal and opposite.

Therefore, it is showed that the equilibrium conditions are satisfied by the components of the forces $F_{Ax}$, $F_{Ay}$ , $F_{Bx}$ and $F_{By}$.