Chapter 14, Problem 56P

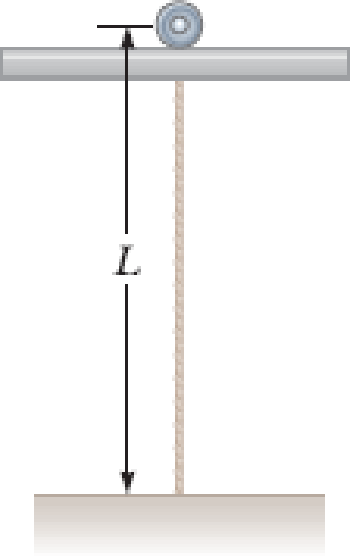
A nylon string has mass 5.50 g and length L = 86.0 cm. The lower end is tied to the floor, and the upper end is tied to a small set of wheels through a slot in a track on which the wheels move (Fig. P14.56). The wheels have a mass that is negligible compared with that of the string, and they roll without friction on the track so that the upper end of the string is essentially free. At equilibrium, the string is vertical and motionless. When it is carrying a small-amplitude wave, you may assume the string is always under uniform tension 1.30 N. (a) Find the speed of transverse waves on the string. (b) The string’s vibration possibilities are a set of standing-wave states, each with a node at the fixed bottom end and an anti-node at the free top end. Find the node–antinode distances for each of the three simplest states. (c) Find the frequency of each of these states.

Figure P14.56

To determine

The speed with which the transverse waves travel

Answer to Problem 56P

The speed of the transverse waves is $14.3\text{m/s}$.

Explanation of Solution

Write the equation for the speed of the transverse wave.

    $v=\sqrt{\frac{T}{\mu }}$        (I)

Here, $T$ is the tension on the string and $\mu$ is the mass per unit length of the string.

Write the equation for the mass per unit length of the string.

    $\mu =\frac{m}{L}$

Here, $m$ is the mass of the string and $L$ is the length of the string. Substitute $5.50\times {10}^{-3}\text{kg}$ for $m$ and $0.86\text{m}$ for $L$.

    $\begin{array}{c}\mu =\frac{5.50\times {10}^{-3}\text{kg}}{0.86\text{m}}\\ =6.40\times {10}^{-3}\text{kg/m}\end{array}$

Conclusion:

Substitute $1.30\text{kg}{\text{.m/s}}^{\text{2}}$ for $T$ and $6.40\times {10}^{-3}\text{kg/m}$ for $\mu$.

    $\begin{array}{c}v=\sqrt{\frac{1.30\text{kg}{\text{.m/s}}^{\text{2}}}{6.40\times {10}^{-3}\text{kg/m}}}\\ =14.3\text{m/s}\end{array}$

Therefore, the speed of the transverse waves is $14.3\text{m/s}$.

To determine

The distance between the node and the antinode

Answer to Problem 56P

The node-antinode distance for the three simplest states is $86.0\text{cm}$, $28.7\text{cm}$ and $17.2\text{cm}$.

Explanation of Solution

The distance between an adjacent node and antinode is on-quarter of a wavelength of the standing wave. There can only be odd number of node-antinode pairs as there is a node at the bottom and an antinode at the top.

Conclusion:

The simplest pattern is one node-antinode pair given as $AN$. Here $A$ represents an antinode and $N$ represents a node. Write the equation for the distance between the node and antinode in the simplest pattern.

    $\frac{{\lambda }_1}{4}=L$

Here, ${\lambda }_1$ is the wavelength corresponding to the simplest pattern and $L$ is the length of the string. Substitute $86.0\text{cm}$ for $L$.

    $\frac{{\lambda }_1}{4}=L=86.0\text{cm}$        (II)

The next simplest pattern is three node-antinode pairs given as $ANAN=AN+NA+AN$. Here, the first $AN$ is the distance between the antinode and the next node, $NA$ is the distance between the node in first $AN$ and the successive antinode and the last $AN$ is the distance between the antinode in $NA$ to the successive node.

Therefore, there are three node-antinode pairs. Write the equation for the distance between the node and antinode in this pattern of three pairs.

    $\begin{array}{c}3\frac{{\lambda }_3}{4}=L\\ \frac{{\lambda }_3}{4}=\frac{L}{3}\end{array}$

Here, ${\lambda }_3$ is the wavelength corresponding to the pattern containing three node-antinode pairs and $L$ is the length of the string. Substitute $86.0\text{cm}$ for $L$.

    $\begin{array}{c}\frac{{\lambda }_3}{4}=\frac{86.0\text{cm}}{3}\\ =28.7\text{cm}\end{array}$        (III)

Similarly, the next simplest pattern is $ANANAN$ with five node-antinode pairs. Write the equation for the distance between the node and antinode in this pattern of five pairs.

    $\begin{array}{c}5\frac{{\lambda }_5}{4}=L\\ \frac{{\lambda }_5}{4}=\frac{L}{5}\end{array}$

Here, ${\lambda }_5$ is the wavelength corresponding to the pattern containing five node-antinode pairs and $L$ is the length of the string. Substitute $86.0\text{cm}$ for $L$.

    $\begin{array}{c}\frac{{\lambda }_5}{4}=\frac{86.0\text{cm}}{5}\\ =17.2\text{cm}\end{array}$        (IV)

Therefore, from equation (II), equation (III) and equation (IV), the node-antinode distance for the three simplest states is $86.0\text{cm}$, $28.7\text{cm}$ and $17.2\text{cm}$ respectively.

To determine

The frequency of the simplest states

Answer to Problem 56P

The frequency of the each of the simplest states is $4.14\text{Hz}$, $12.4\text{Hz}$ and $20.7\text{Hz}$.

Explanation of Solution

Write the equation for the frequency of the states.

    $f_n=\frac{v}{4\left(\frac{{\lambda }_n}{4}\right)}$        (V)

Here, $v$ is the speed of the transverse waves and ${\lambda }_n$ is the wavelength corresponding to the number of node-antinode pairs.

Conclusion:

Substitute $1$ for $n$ in equation (V) to find the frequency corresponding to one node-antinode pair.

    $f_1=\frac{v}{4\left(\frac{{\lambda }_1}{4}\right)}$        (VI)

Substitute equation (II) in equation (VI) and also $14.3\text{m/s}$ for $v$.

    $\begin{array}{c}{f}_1=\frac{14.3\text{m/s}}{4\left(0.860\text{m}\right)}\\ =4.14\text{Hz}\end{array}$        (VII)

Substitute $3$ for $n$ in equation (V) to find the frequency corresponding to three node-antinode pairs.

    $f_3=\frac{v}{4\left(\frac{{\lambda }_3}{4}\right)}$        (VIII)

Substitute equation (III) in equation (VIII) and also $14.3\text{m/s}$ for $v$.

    $\begin{array}{c}{f}_3=\frac{14.3\text{m/s}}{4\left(0.287\text{m}\right)}\\ =12.4\text{Hz}\end{array}$        (IX)

Substitute $5$ for $n$ in equation (V) to find the frequency corresponding to five node-antinode pairs.

    $f_5=\frac{v}{4\left(\frac{{\lambda }_5}{4}\right)}$        (X)

Substitute equation (IV) in equation (X) and also $14.3\text{m/s}$ for $v$.

    $\begin{array}{c}{f}_3=\frac{14.3\text{m/s}}{4\left(0.172\text{m}\right)}\\ =20.7\text{Hz}\end{array}$        (XI)

Therefore, from equation (VII), equation (IX) and equation (XI), the frequency of the simplest states is $4.14\text{Hz}$, $12.4\text{Hz}$ and $20.7\text{Hz}$ respectively.