
Concept explainers
Children playing pirates have suspended a uniform wooden plank with mass 15.0 kg and length 2.50 m as shown in Figure P14.27. What is the tension in each of the three ropes when Sophia, with a mass of 23.0 kg, is made to “walk the plank” and is 1.50 m from reaching the end of the plank?
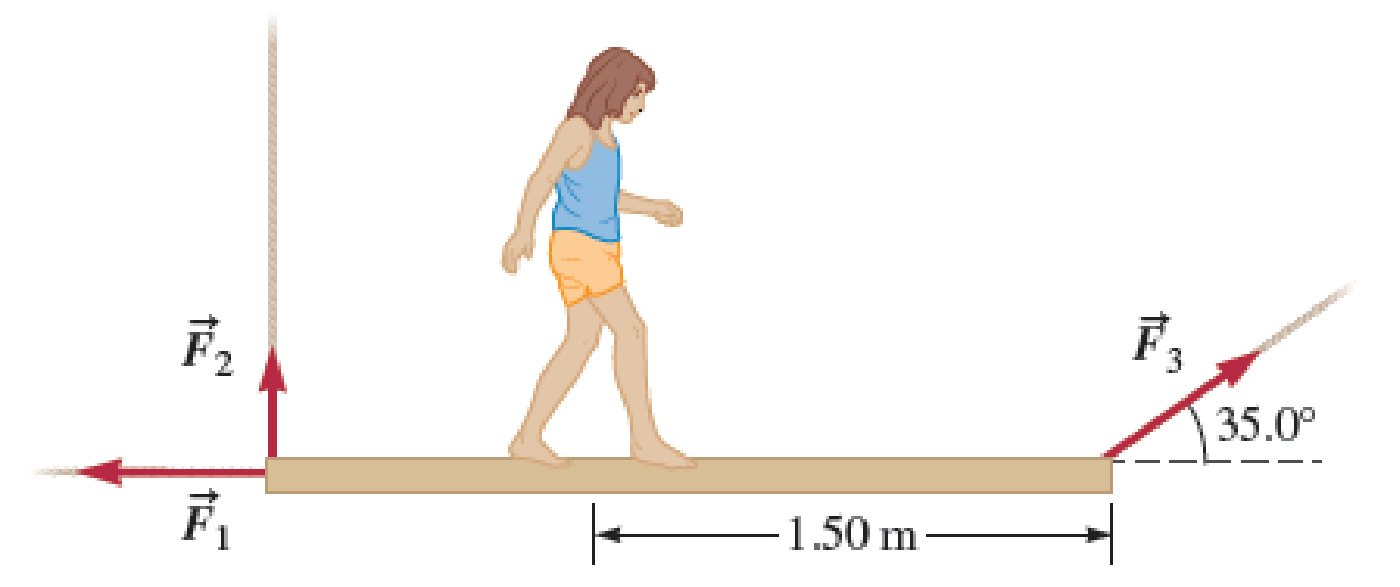
FIGURE P14.27
The tension in each of the three ropes when S with mass of
Answer to Problem 27PQ
The tension in rope1 is
Explanation of Solution
The free body diagram is given below.
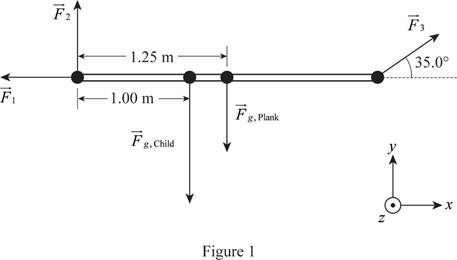
Here,
At equilibrium, the sum of forces and sum of torques must be zero.
Consider torque about an axis perpendicular to the page and through the left end of the plank.
Write the equilibrium condition for the torque about an axis perpendicular to the page and through the left end of the plank.
Here,
Since forces
Write the expression for the torque due to a force.
Here,
The forces
Write expression for the net torque about an axis perpendicular to the page and through the left end of the plank.
Here,
Write the expression for
Here,
Write the expression for
Here,
Substitute equation (III) and (IV) in (II) to get
Substitute above equation in equation (I) to get expression for
Write the equilibrium condition of the force along
Here,
Write expression for net force along
Here,
Substitute (VII) in (VI) to get
Write the equilibrium condition of the forces along
Here,
Write net forces along
Here,
Substitute (III) and (IV)in (X) to get
Substitute (XI) in (IX) to get
Conclusion:
Substitute
Substitute
Substitute
Therefore, the tension in rope1 is
Want to see more full solutions like this?
Chapter 14 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Consider 1 mole of supercooled water at -10°C. Calculate the entropy change of the water when the supercooled water freezes at -10°C and 1 atm. Useful data: Cp (ice) = 38 J mol-1 K-1 Cp (water) 75J mol −1 K -1 Afus H (0°C) 6026 J mol −1 Assume Cp (ice) and Cp (water) to be independent of temperature.arrow_forwardThe molar enthalpy of vaporization of benzene at its normal boiling point (80.09°C) is 30.72 kJ/mol. Assuming that AvapH and AvapS stay constant at their values at 80.09°C, calculate the value of AvapG at 75.0°C, 80.09°C, and 85.0°C. Hint: Remember that the liquid and vapor phases will be in equilibrium at the normal boiling point.arrow_forward3. The entropy of an ideal gas is S = Nkg In V. Entropy is a state function rather than a path function, and in this problem, you will show an example of the entropy change for an ideal gas being the same when you go between the same two states by two different pathways. A. Express ASV = S2 (V2) - S₁(V1), the change in entropy upon changing the volume from V₁to V2, at fixed particle number N and energy, U. B. Express ASN = S₂(N₂) - S₁ (N₁), the change in entropy upon changing the particle number from N₁ to N2, at fixed volume V and energy U. C. Write an expression for the entropy change, AS, for a two-step process (V₁, N₁) → (V2, N₁) → (V2, N₂) in which the volume changes first at fixed particle number, then the particle number changes at fixed volume. Again, assume energy is constant.arrow_forward
- Please don't use Chatgpt will upvote and give handwritten solutionarrow_forward6. We used the constant volume heat capacity, Cv, when we talked about thermodynamic cycles. It acts as a proportionality constant between energy and temperature: dU = C₁dT. You can also define a heat capacity for constant pressure processes, Cp. You can think of enthalpy playing a similar role to energy, but for constant pressure processes δαρ C = (37) - Sup Ср ат P = ат Starting from the definition of enthalpy, H = U + PV, find the relationship between Cy and Cp for an ideal gas.arrow_forwardPure membranes of dipalmitoyl lecithin phospholipids are models of biological membranes. They melt = 41°C. Reversible melting experiments indicate that at Tm AHm=37.7 kJ mol-1. Calculate: A. The entropy of melting, ASm- B. The Gibbs free energy of melting, AGm- C. Does the membrane become more or less ordered upon melting? D. There are 32 rotatable CH2 CH2 bonds in each molecule that can rotate more freely if the membrane melts. What is the increase in multiplicity on melting a mole of bonds?arrow_forward
- 5. Heat capacity often has a temperature dependence for real molecules, particularly if you go over a large temperature range. The heat capacity for liquid n-butane can be fit to the equation Cp(T) = a + bT where a = 100 J K₁₁ mol¹ and b = 0.1067 J K² mol¹ from its freezing point (T = 140 K) to its boiling point (T₁ = 270 K). A. Compute AH for heating butane from 170 K to 270 K. B. Compute AS for the same temperature range.arrow_forward4. How much energy must be transferred as heat to cause the quasi-static isothermal expansion of one mole of an ideal gas at 300 K from PA = 1 bar to PB = 0.5 bar? A. What is VA? B. What is VB? C. What is AU for the process? D. What is AH for the process? E. What is AS for the process?arrow_forward1. The diagram shows the tube used in the Thomson experiment. a. State the KE of the electrons. b. Draw the path of the electron beam in the gravitational field of the earth. C. If the electric field directed upwards, deduce the direction of the magnetic field so it would be possible to balance the forces. electron gun 1KVarrow_forward
- as a hiker in glacier national park, you need to keep the bears from getting at your food supply. You find a campground that is near an outcropping of ice. Part of the outcropping forms a feta=51.5* slopeup that leads to a verticle cliff. You decide that this is an idea place to hang your food supply out of bear reach. You put all of your food into a burlap sack, tie a rope to the sack, and then tie a bag full of rocks to the other end of the rope to act as an anchor. You currently have 18.5 kg of food left for the rest of your trip, so you put 18.5 kg of rocks in the anchor bag to balance it out. what happens when you lower the food bag over the edge and let go of the anchor bag? Determine the acceleration magnitude a of the two-bag system when you let go of the anchor bag?arrow_forward2. A thin Nichrome wire is used in an experiment to test Ohm's law using a power supply ranging from 0 to 12 V in steps of 2 V. Why isn't the graph of I vs V linear? 1. Nichrome wire does obey Ohm's law. Explain how that can that be true given the results abovearrow_forward1. The average KE and temperature in Kelvin of the molecules of a gas are related by the equation KE = 3/2 KT where k is the Boltzmann constant 1.38 x 10 m² kg s². The diagram shows the energy levels for a Hydrogen atom. Energy/eV 0.00 -1.51 3.39 13.58 Use this information to show that Hydrogen at room temperature will not emit light. 2. When hydrogen burns in oxygen 241.8 kJ of energy are released per mole. Show that this reaction can produce light.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





