
Concept explainers
The keystone of an arch is the stone at the top (Fig. P14.9). It is supported by forces from its two neighbors, blocks A and B. Each block has mass m and approximate length L. What can you conclude about the force exerted by each block,
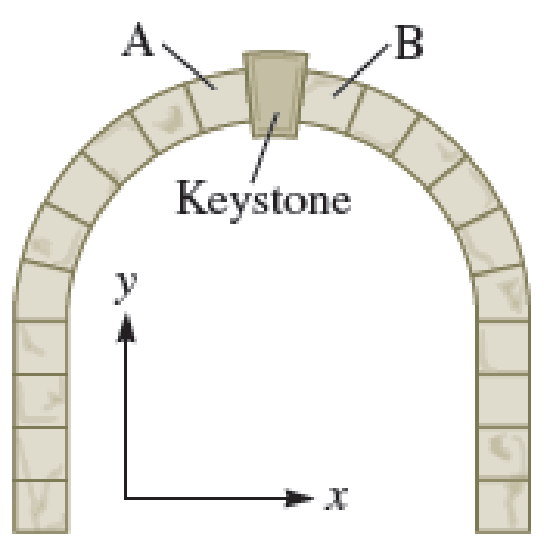
FIGURE P14.9
To show that the equilibrium conditions are satisfied by the components of the forces
Answer to Problem 9PQ
It is showed that the equilibrium conditions are satisfied by the components of the forces
Explanation of Solution
A body remains in static equilibrium if net force and torque is equal to zero.
The forces acting on the keystone are force from block A , force from block B and force of gravity, which points downward.
Write the expression for the net force acting on the keystone by block A.
Here,
Write the expression for the net force acting on the keystone by block B.
Here,
Write the expression for the force of gravity on Keystone.
Here,
It is given that Keystone is in static equilibrium.
Write the equilibrium condition for the forces along
Here,
Expand above equation using components of forces along
Rearrange above equation to get
Write the equilibrium condition for the forces along
Here,
Expand above equation using components of forces along
Assume that arch is symmetric.
Substitute
Put the above equation in equation (IX).
Substitute
Substitute
Write the expression for the torque acting on the keystone due to force
Here,
It is given that length of each block is
Write the expression for
Substitute
Use expressions
Write the expression for the torque acting on the keystone due to force
Here,
Write the expression for
Substitute
Use expressions
Thus, torque
Conclusion:
From above calculations it is clear that, net force and net torque are zero if
Each of the neighboring block supports half the weight of the keystone and the forces in the
Therefore, it is showed that the equilibrium conditions are satisfied by the components of the forces
Want to see more full solutions like this?
Chapter 14 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- In general it is best to conceptualize vectors as arrows in space, and then to make calculations with them using their components. (You must first specify a coordinate system in order to find the components of each arrow.) This problem gives you some practice with the components. Let vectors A = (1,0, -3), B = (-2, 5, 1), and C = (3,1,1). Calculate the following, and express your answers as ordered triplets of values separated by commas.arrow_forwardIn general it is best to conceptualize vectors as arrows in space, and then to make calculations with them using their components. (You must first specify a coordinate system in order to find the components of each arrow.) This problem gives you some practice with the components. Let vectors A = (1,0, −3), B = (-2, 5, 1), and C = (3,1,1). Calculate the following, and express your answers as ordered triplets of values separated by commas.arrow_forwardOnly Part C.) is necessaryarrow_forward
- Only Part B.) is necessaryarrow_forwardA (3.60 m) 30.0°- 70.0° x B (2.40 m)arrow_forwardIn general it is best to conceptualize vectors as arrows in space, and then to make calculations with them using their components. (You must first specify a coordinate system in order to find the components of each arrow.) This problem gives you some practice with the components. Let vectors A = (1,0, -3), B = (-2, 5, 1), and C = (3,1,1). Calculate the following, and express your answers as ordered triplets of values separated by commas.arrow_forward
- fine the magnitude of the vector product express in sq meters what direction is the vector product in -z or +zarrow_forward4) Three point charges of magnitude Q1 = +2.0 μC, Q2 = +3.0 μС, Q3 = = +4.0 μС are located at the corners of a triangle as shown in the figure below. Assume d = 20 cm. (a) Find the resultant force vector acting on Q3. (b) Find the magnitude and direction of the force. d Q3 60° d Q1 60° 60° Q2 darrow_forwardThree point charges of magnitudes Q₁ = +6.0 μС, Q₂ = −7.0 μС, Qз = −13.0 μC are placed on the x-axis at x = 0 cm, x = 40 cm, and x = 120 cm, respectively. What is the force on the Q3 due to the other two charges?arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University





