Modeling the Dynamics of Life: Calculus and Probability for Life Scientists
3rd Edition
ISBN: 9780840064189
Author: Frederick R. Adler
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 1.4, Problem 18E
To determine
To Compute the values of the functions at the points indicated and Sketch its graph.
Expert Solution & Answer
Answer to Problem 18E
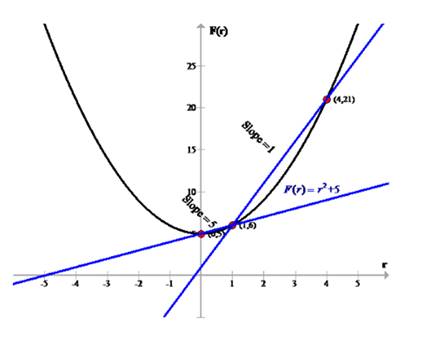
The slope between the points r=0 and r=1 of the given function is 1.
Furthermore, the slope between the points r=1 and r=4 of the given function is 5.
Hence, the slope of the given function is not constant.
Explanation of Solution
Given:
The function
The given input points are as follows:
r=0
r=1
r=4
Consider the function
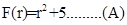
The given input points are as follows:
r=0
r=1
r=4
The slope between the input points r1 and r1 with output F(r1) and F(r2) , respectively is
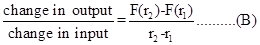
Consider the value of function at the following points:
At r=0, we get
At r=1, we find that
At r=4, we have
Therefore, the value of the function at the points r=0, r=1, and r=4, respectively are
The slope between the points r=0 and r=1 of function (A) using formula (B) is shown below:
The slope between points r=1 and r=4 of function (A) using formula (B) is as follows:
Therefore, the slope between the points r=0 and r=1 of the given function (A) is 1.
Furthermore, the slope between the points r=1 and r=4 of the given function (A) is 5.
By determining the slopes between the points r=0 , r=1, r=4, we get different values of slopes.
Hence, the slope of the given function is not contant.
The graph of the function is shown below:
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
5. (a) State the Residue Theorem. Your answer should include all the conditions required
for the theorem to hold.
(4 marks)
(b) Let y be the square contour with vertices at -3, -3i, 3 and 3i, described in the
anti-clockwise direction. Evaluate
に
dz.
You must check all of the conditions of any results that you use.
(5 marks)
(c) Evaluate
L
You must check all of the conditions of any results that you use.
ཙ
x sin(Tx)
x²+2x+5
da.
(11 marks)
3. (a) Lety: [a, b] C be a contour. Let L(y) denote the length of y. Give a formula
for L(y).
(1 mark)
(b) Let UCC be open. Let f: U→C be continuous. Let y: [a,b] → U be a
contour. Suppose there exists a finite real number M such that |f(z)| < M for
all z in the image of y. Prove that
<
||, f(z)dz| ≤ ML(y).
(3 marks)
(c) State and prove Liouville's theorem. You may use Cauchy's integral formula without
proof.
(d) Let R0. Let w € C. Let
(10 marks)
U = { z Є C : | z − w| < R} .
Let f UC be a holomorphic function such that
0 < |ƒ(w)| < |f(z)|
for all z Є U. Show, using the local maximum modulus principle, that f is constant.
(6 marks)
3. (a) Let A be an algebra. Define the notion of an A-module M. When is a module M
a simple module?
(b) State and prove Schur's Lemma for simple modules.
(c) Let AM(K) and M = K" the natural A-module.
(i) Show that M is a simple K-module.
(ii) Prove that if ƒ € Endд(M) then ƒ can be written as f(m) = am, where a
is a matrix in the centre of M, (K).
[Recall that the centre, Z(M,(K)) == {a Mn(K) | ab
M,,(K)}.]
= ba for all bЄ
(iii) Explain briefly why this means End₁(M) K, assuming that Z(M,,(K))~
K as K-algebras.
Is this consistent with Schur's lemma?
Chapter 1 Solutions
Modeling the Dynamics of Life: Calculus and Probability for Life Scientists
Ch. 1.2 - Identify the variables and parameters in the...Ch. 1.2 - Prob. 2ECh. 1.2 - Compute the values of the following functions at...Ch. 1.2 - Compute the values of the following functions at...Ch. 1.2 - Compute the values of the following functions at...Ch. 1.2 - Compute the values of the following functions at...Ch. 1.2 - Graph the given points and say which point does...Ch. 1.2 - Graph the given points and say which point does...Ch. 1.2 - Graph the given points and say which point does...Ch. 1.2 - Graph the given points and say which point does...
Ch. 1.2 - Evaluate the following functions at the given...Ch. 1.2 - Evaluate the following functions at the given...Ch. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Find the inverses of each of the following...Ch. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Graph each of the following functions and its...Ch. 1.2 - Graph each of the following functions and its...Ch. 1.2 - Graph each of the following functions and its...Ch. 1.2 - Prob. 33ECh. 1.2 - Find the compositions of the given functions....Ch. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - The following series of functional compositions...Ch. 1.2 - The following series of functional compositions...Ch. 1.2 - The following series of functional compositions...Ch. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - Prob. 3ECh. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Find the mass in kilograms of the following...Ch. 1.3 - Prob. 34ECh. 1.3 - Change the units in the following functions, and...Ch. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.4 - For the following lines, find the slopes between...Ch. 1.4 - Prob. 2ECh. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - The following data give the elevation of the...Ch. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - Prob. 56ECh. 1.4 - Prob. 57ECh. 1.4 - Prob. 58ECh. 1.4 - Prob. 59ECh. 1.4 - Prob. 60ECh. 1.5 - Write the updating function associated with each...Ch. 1.5 - Write the updating function associated with each...Ch. 1.5 - Write the updating function associated with each...Ch. 1.5 - Write the updating function associated with each...Ch. 1.5 - Compose the updating function associated with each...Ch. 1.5 - Compose the updating function associated with each...Ch. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - Prob. 14ECh. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Use the formula for the solution to find the...Ch. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.5 - Prob. 52ECh. 1.5 - Prob. 53ECh. 1.5 - Prob. 54ECh. 1.5 - Prob. 55ECh. 1.5 - Prob. 56ECh. 1.5 - Prob. 57ECh. 1.5 - Prob. 58ECh. 1.5 - Prob. 59ECh. 1.5 - Prob. 60ECh. 1.5 - Prob. 61ECh. 1.5 - Prob. 62ECh. 1.6 - The following steps are used to build a cobweb...Ch. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Find the equilibria of the following discrete-time...Ch. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Cobweb and find the equilibrium of the following...Ch. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - Prob. 9ECh. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - Prob. 14ECh. 1.7 - Prob. 15ECh. 1.7 - Prob. 16ECh. 1.7 - Prob. 17ECh. 1.7 - Use the laws of logs to rewrite the following if...Ch. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - Prob. 36ECh. 1.7 - Prob. 37ECh. 1.7 - Prob. 38ECh. 1.7 - Prob. 39ECh. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Prob. 42ECh. 1.7 - Prob. 43ECh. 1.7 - Prob. 44ECh. 1.7 - Prob. 45ECh. 1.7 - Prob. 46ECh. 1.7 - Prob. 47ECh. 1.7 - Prob. 48ECh. 1.7 - Prob. 49ECh. 1.7 - Prob. 50ECh. 1.7 - Prob. 51ECh. 1.7 - Prob. 52ECh. 1.7 - Prob. 53ECh. 1.7 - Prob. 54ECh. 1.7 - Prob. 55ECh. 1.7 - Prob. 56ECh. 1.7 - Prob. 57ECh. 1.7 - Prob. 58ECh. 1.7 - Prob. 59ECh. 1.7 - Prob. 60ECh. 1.7 - Prob. 61ECh. 1.7 - Prob. 62ECh. 1.7 - Prob. 63ECh. 1.7 - Prob. 64ECh. 1.7 - Prob. 65ECh. 1.7 - Prob. 66ECh. 1.7 - Prob. 67ECh. 1.7 - Prob. 68ECh. 1.7 - Prob. 69ECh. 1.7 - Prob. 70ECh. 1.7 - Prob. 71ECh. 1.7 - Prob. 72ECh. 1.7 - Prob. 73ECh. 1.8 - Prob. 1ECh. 1.8 - Prob. 2ECh. 1.8 - Prob. 3ECh. 1.8 - Prob. 4ECh. 1.8 - Prob. 5ECh. 1.8 - Prob. 6ECh. 1.8 - Prob. 7ECh. 1.8 - Prob. 8ECh. 1.8 - Prob. 9ECh. 1.8 - Prob. 10ECh. 1.8 - Prob. 11ECh. 1.8 - Prob. 12ECh. 1.8 - Prob. 13ECh. 1.8 - Prob. 14ECh. 1.8 - Prob. 15ECh. 1.8 - Prob. 16ECh. 1.8 - Prob. 17ECh. 1.8 - Prob. 18ECh. 1.8 - Prob. 19ECh. 1.8 - Prob. 20ECh. 1.8 - Prob. 21ECh. 1.8 - Prob. 22ECh. 1.8 - Prob. 23ECh. 1.8 - Prob. 24ECh. 1.8 - Prob. 25ECh. 1.8 - Prob. 26ECh. 1.8 - Prob. 27ECh. 1.8 - Prob. 28ECh. 1.8 - Prob. 29ECh. 1.8 - Prob. 30ECh. 1.8 - Prob. 31ECh. 1.8 - Prob. 32ECh. 1.8 - Prob. 33ECh. 1.8 - Prob. 34ECh. 1.8 - Prob. 35ECh. 1.8 - Prob. 36ECh. 1.8 - Prob. 37ECh. 1.8 - Prob. 38ECh. 1.8 - Prob. 39ECh. 1.8 - Prob. 40ECh. 1.8 - Prob. 41ECh. 1.8 - Prob. 42ECh. 1.8 - Prob. 43ECh. 1.8 - Prob. 44ECh. 1.8 - Prob. 45ECh. 1.8 - Prob. 46ECh. 1.8 - Prob. 47ECh. 1.8 - Prob. 48ECh. 1.8 - Prob. 49ECh. 1.8 - Prob. 50ECh. 1.8 - Prob. 51ECh. 1.9 - Prob. 1ECh. 1.9 - Prob. 2ECh. 1.9 - Prob. 3ECh. 1.9 - Prob. 4ECh. 1.9 - Prob. 5ECh. 1.9 - Prob. 6ECh. 1.9 - Prob. 7ECh. 1.9 - Prob. 8ECh. 1.9 - Prob. 9ECh. 1.9 - Prob. 10ECh. 1.9 - Prob. 11ECh. 1.9 - Prob. 12ECh. 1.9 - Prob. 13ECh. 1.9 - Prob. 14ECh. 1.9 - Prob. 15ECh. 1.9 - Prob. 16ECh. 1.9 - Prob. 17ECh. 1.9 - Prob. 18ECh. 1.9 - Prob. 19ECh. 1.9 - Prob. 20ECh. 1.9 - Prob. 21ECh. 1.9 - Prob. 22ECh. 1.9 - Prob. 23ECh. 1.9 - Prob. 24ECh. 1.9 - Prob. 25ECh. 1.9 - Prob. 26ECh. 1.9 - Prob. 27ECh. 1.9 - Prob. 28ECh. 1.9 - Prob. 29ECh. 1.9 - Prob. 30ECh. 1.9 - Prob. 31ECh. 1.9 - Prob. 32ECh. 1.9 - Prob. 33ECh. 1.9 - Prob. 34ECh. 1.9 - Prob. 35ECh. 1.9 - Prob. 36ECh. 1.9 - Prob. 37ECh. 1.9 - Prob. 38ECh. 1.9 - Prob. 39ECh. 1.9 - Prob. 40ECh. 1.9 - Prob. 41ECh. 1.9 - Prob. 42ECh. 1.9 - Prob. 43ECh. 1.9 - Prob. 44ECh. 1.9 - Prob. 45ECh. 1.9 - Prob. 46ECh. 1.9 - Prob. 47ECh. 1.9 - Prob. 48ECh. 1.9 - Prob. 49ECh. 1.9 - Prob. 50ECh. 1.9 - Prob. 51ECh. 1.10 - A population consists of 200 red birds and 800...Ch. 1.10 - A population consists of 200 red birds and 800...Ch. 1.10 - A population consists of 200 red birds and 800...Ch. 1.10 - Prob. 4ECh. 1.10 - Prob. 5ECh. 1.10 - Prob. 6ECh. 1.10 - Prob. 7ECh. 1.10 - Prob. 8ECh. 1.10 - Prob. 9ECh. 1.10 - Prob. 10ECh. 1.10 - Prob. 11ECh. 1.10 - Prob. 12ECh. 1.10 - Prob. 13ECh. 1.10 - Prob. 14ECh. 1.10 - Prob. 15ECh. 1.10 - Prob. 16ECh. 1.10 - Prob. 17ECh. 1.10 - Prob. 18ECh. 1.10 - Prob. 19ECh. 1.10 - Prob. 20ECh. 1.10 - Prob. 21ECh. 1.10 - Prob. 22ECh. 1.10 - Prob. 23ECh. 1.10 - Prob. 24ECh. 1.10 - Prob. 25ECh. 1.10 - Prob. 26ECh. 1.10 - Prob. 27ECh. 1.10 - Prob. 28ECh. 1.10 - Prob. 29ECh. 1.10 - Prob. 30ECh. 1.10 - Prob. 31ECh. 1.10 - Prob. 32ECh. 1.10 - Prob. 33ECh. 1.10 - Prob. 34ECh. 1.10 - Prob. 35ECh. 1.10 - The model of selection studied in this section is...Ch. 1.10 - Prob. 37ECh. 1.10 - Prob. 38ECh. 1.10 - Prob. 39ECh. 1.10 - Prob. 40ECh. 1.10 - Prob. 41ECh. 1.10 - Prob. 42ECh. 1.10 - Prob. 43ECh. 1.10 - Prob. 44ECh. 1.10 - Prob. 45ECh. 1.10 - Prob. 46ECh. 1.10 - Prob. 47ECh. 1.10 - Prob. 48ECh. 1.10 - Prob. 49ECh. 1.11 - Prob. 1ECh. 1.11 - Prob. 2ECh. 1.11 - Prob. 3ECh. 1.11 - Prob. 4ECh. 1.11 - Prob. 5ECh. 1.11 - Prob. 6ECh. 1.11 - Prob. 7ECh. 1.11 - Prob. 8ECh. 1.11 - Prob. 9ECh. 1.11 - Prob. 10ECh. 1.11 - Prob. 11ECh. 1.11 - Prob. 12ECh. 1.11 - Prob. 13ECh. 1.11 - Prob. 14ECh. 1.11 - Prob. 15ECh. 1.11 - Prob. 16ECh. 1.11 - Prob. 17ECh. 1.11 - Prob. 18ECh. 1.11 - Prob. 19ECh. 1.11 - Prob. 20ECh. 1 - Suppose you have a culture of bacteria, where the...Ch. 1 - Prob. 2SPCh. 1 - Prob. 3SPCh. 1 - A lab has a culture of a new kind of bacteria...Ch. 1 - Prob. 5SPCh. 1 - Prob. 6SPCh. 1 - Prob. 7SPCh. 1 - Prob. 8SPCh. 1 - Prob. 9SPCh. 1 - Prob. 10SPCh. 1 - A person develops a small liver tumor. It grows...Ch. 1 - Prob. 12SPCh. 1 - Prob. 13SPCh. 1 - Prob. 14SPCh. 1 - Prob. 15SPCh. 1 - Prob. 16SPCh. 1 - Prob. 17SPCh. 1 - Prob. 18SPCh. 1 - Prob. 19SPCh. 1 - Prob. 20SPCh. 1 - Prob. 21SPCh. 1 - Prob. 22SPCh. 1 - Prob. 23SPCh. 1 - Prob. 24SPCh. 1 - Prob. 25SPCh. 1 - Prob. 26SPCh. 1 - Prob. 27SPCh. 1 - Prob. 28SPCh. 1 - Prob. 29SP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- (a) State, without proof, Cauchy's theorem, Cauchy's integral formula and Cauchy's integral formula for derivatives. Your answer should include all the conditions required for the results to hold. (8 marks) (b) Let U{z EC: |z| -1}. Let 12 be the triangular contour with vertices at 0, 2-2 and 2+2i, parametrized in the anticlockwise direction. Calculate dz. You must check the conditions of any results you use. (d) Let U C. Calculate Liz-1ym dz, (z - 1) 10 (5 marks) where 2 is the same as the previous part. You must check the conditions of any results you use. (4 marks)arrow_forward(a) Suppose a function f: C→C has an isolated singularity at wЄ C. State what it means for this singularity to be a pole of order k. (2 marks) (b) Let f have a pole of order k at wЄ C. Prove that the residue of f at w is given by 1 res (f, w): = Z dk (k-1)! >wdzk−1 lim - [(z — w)* f(z)] . (5 marks) (c) Using the previous part, find the singularity of the function 9(z) = COS(πZ) e² (z - 1)²' classify it and calculate its residue. (5 marks) (d) Let g(x)=sin(211). Find the residue of g at z = 1. (3 marks) (e) Classify the singularity of cot(z) h(z) = Z at the origin. (5 marks)arrow_forward1. Let z = x+iy with x, y Є R. Let f(z) = u(x, y) + iv(x, y) where u(x, y), v(x, y): R² → R. (a) Suppose that f is complex differentiable. State the Cauchy-Riemann equations satisfied by the functions u(x, y) and v(x,y). (b) State what it means for the function (2 mark) u(x, y): R² → R to be a harmonic function. (3 marks) (c) Show that the function u(x, y) = 3x²y - y³ +2 is harmonic. (d) Find a harmonic conjugate of u(x, y). (6 marks) (9 marks)arrow_forward
- Let A be a vector space with basis 1, a, b. Which (if any) of the following rules turn A into an algebra? (You may assume that 1 is a unit.) (i) a² = a, b² = ab = ba = 0. (ii) a²=b, b² = ab = ba = 0. (iii) a²=b, b² = b, ab = ba = 0.arrow_forwardNo chatgpt pls will upvotearrow_forward= 1. Show (a) Let G = Z/nZ be a cyclic group, so G = {1, 9, 92,...,g" } with g": that the group algebra KG has a presentation KG = K(X)/(X” — 1). (b) Let A = K[X] be the algebra of polynomials in X. Let V be the A-module with vector space K2 and where the action of X is given by the matrix Compute End(V) in the cases (i) x = p, (ii) xμl. (67) · (c) If M and N are submodules of a module L, prove that there is an isomorphism M/MON (M+N)/N. (The Second Isomorphism Theorem for modules.) You may assume that MON is a submodule of M, M + N is a submodule of L and the First Isomorphism Theorem for modules.arrow_forward
- (a) Define the notion of an ideal I in an algebra A. Define the product on the quotient algebra A/I, and show that it is well-defined. (b) If I is an ideal in A and S is a subalgebra of A, show that S + I is a subalgebra of A and that SnI is an ideal in S. (c) Let A be the subset of M3 (K) given by matrices of the form a b 0 a 0 00 d Show that A is a subalgebra of M3(K). Ꮖ Compute the ideal I of A generated by the element and show that A/I K as algebras, where 0 1 0 x = 0 0 0 001arrow_forward(a) Let HI be the algebra of quaternions. Write out the multiplication table for 1, i, j, k. Define the notion of a pure quaternion, and the absolute value of a quaternion. Show that if p is a pure quaternion, then p² = -|p|². (b) Define the notion of an (associative) algebra. (c) Let A be a vector space with basis 1, a, b. Which (if any) of the following rules turn A into an algebra? (You may assume that 1 is a unit.) (i) a² = a, b²=ab = ba 0. (ii) a² (iii) a² = b, b² = abba = 0. = b, b² = b, ab = ba = 0. (d) Let u1, 2 and 3 be in the Temperley-Lieb algebra TL4(8). ገ 12 13 Compute (u3+ Augu2)² where A EK and hence find a non-zero x € TL4 (8) such that ² = 0.arrow_forwardQ1: Solve the system x + x = t², x(0) = (9)arrow_forward
- Between the function 3 (4)=x-x-1 Solve inside the interval [1,2]. then find the approximate Solution the root within using the bisection of the error = 10² method.arrow_forwardE10) Perform four iterations of the Jacobi method for solving the following system of equations. 2 -1 -0 -0 XI 2 0 0 -1 2 X3 0 0 2 X4 With x(0) (0.5, 0.5, 0.5, 0.5). Here x = (1, 1, 1, 1)". How good x (5) as an approximation to x?arrow_forwardby (2) Gauss saidel - - method find (2) و X2 for the sestem X1 + 2x2=-4 2x1 + 2x2 = 1 Such thef (0) x2=-2arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY