MASTERINGPHYSICS W/ETEXT ACCESS CODE 6
13th Edition
ISBN: 9781269542661
Author: YOUNG
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
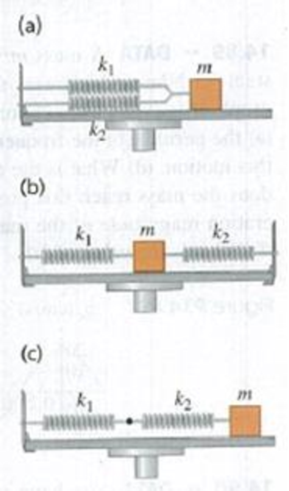
Chapter 14, Problem 14.92CP
The Effective Force Constant of Two Springs. Two springs with the same unstretched length hut different force constants k1 and k2 are attached to a block with mass m on a level, frictionless surface. Calculate the effective force constant keff in each of the three cases (a), (b), and (c) depicted in Fig. P14.92. (The effective force constant is defined by ΣFx = −keffx.) (d) An object with mass m, suspended from a uniform spring with a force constant k, vibrates with a frequency f1. When the spring is cut in half and the same object is suspended from one of the halves, the frequency is f2. What is the ratio f1/f2?
Figure P14.92
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A surgeon is using material from a donated heart to repair a patient's damaged aorta and needs to know the elastic characteristics of this aortal material. Tests performed on a 16.0 em strip of the donated aorta reveal that it stretches 3.75 cm when a 1.50 N pull is exerted on it. (a) What is the force constant of this strip of aortal material? (b) If the maximum distance it will be able to stretch when it replaces the aorta in the damaged heart is 1.14 cm, what is the greatest force it will be able to exert there?
A biomechanical model of the bones and biceps muscles of a person's arm supporting a mass
m=2 kg is shown below. The weight of the forearm is 9 N. If the cross section of the tendon AB is 28
mm? what is the average normai stress in the tendon? u
290 mm
50 mm
200 mm
150 mm
The bonded single lap joint shown below has a width, w = 97 mm and an overlap length, I = 28 mm.
It has an applied tensile load, F. of 4385 N and a layer of adhesive h = 1.1 mm thick between the
two members. The shear modulus of the adhesive is G = 3.7 GPa.
W
x-direction
(a) What is the shear strain in the adhesive? Give your answer in radians, to 2 s.f.
Shear strain:
rad
(b) Assuming that there is no deformation in the wooden sheets, what is the displacement of the upper
plate in the x-direction? Give your answer in millimetres, to 2 s.f
Displacement:
mm
Chapter 14 Solutions
MASTERINGPHYSICS W/ETEXT ACCESS CODE 6
Ch. 14.1 - A body like that shown in Fig. 14.2 oscillates...Ch. 14.2 - A glider is attached to a spring as shown in Fig....Ch. 14.3 - (a) To double the total energy for a mass-spring...Ch. 14.4 - A block attached to a hanging ideal spring...Ch. 14.5 - When a body oscillating on a horizontal spring...Ch. 14.6 - The center of gravity of a simple pendulum of mass...Ch. 14.7 - An airplane is flying in a straight line at a...Ch. 14.8 - When driven at a frequency near its natural...Ch. 14 - An object is moving with SHM of amplitude A on the...Ch. 14 - Think of several examples in everyday life of...
Ch. 14 - Does a tuning fork or similar tuning instrument...Ch. 14 - A box containing a pebble is attached to an ideal...Ch. 14 - If a uniform spring is cut in half, what is the...Ch. 14 - A glider is attached to a fixed ideal spring and...Ch. 14 - Two identical gliders on an air track are...Ch. 14 - You are captured by Martians, taken into their...Ch. 14 - The system shown in Fig. 14.17 is mounted in an...Ch. 14 - If a pendulum has a period of 2.5 s on earth, what...Ch. 14 - A simple pendulum is mounted in an elevator. What...Ch. 14 - What should you do to the length of the string of...Ch. 14 - If a pendulum clock is taken to a mountaintop,...Ch. 14 - When the amplitude of a simple pendulum increases,...Ch. 14 - Prob. 14.15DQCh. 14 - At what point in the motion of a simple pendulum...Ch. 14 - Could a standard of time be based on the period of...Ch. 14 - For a simple pendulum, clearly distinguish between...Ch. 14 - In designing structures in an earthquake-prone...Ch. 14 - BIO (a) Music. When a person sings, his or her...Ch. 14 - If an object on a horizontal, frictionless surface...Ch. 14 - The tip of a tuning fork goes through 440 complete...Ch. 14 - The displacement of an oscillating object as a...Ch. 14 - A machine part is undergoing SUM with a frequency...Ch. 14 - BIO The wings of the blue-throated hummingbird...Ch. 14 - A 2.40-kg ball is attached to an unknown spring...Ch. 14 - In a physics lab, you attach a 0.200-kg air-track...Ch. 14 - When a body of unknown mass is attached to an...Ch. 14 - When a 0.750-kg mass oscillates on an ideal...Ch. 14 - An object is undergoing SHM with period 0.900 s...Ch. 14 - A small block is attached to an ideal spring and...Ch. 14 - A 2.00-kg. frictionless block is attached to an...Ch. 14 - Repeat Exercise 14.13, but assume that at t = 0...Ch. 14 - The point of the needle of a sewing machine moves...Ch. 14 - A small block is attached to an ideal spring and...Ch. 14 - BIO Weighing Astronauts. This procedure has been...Ch. 14 - A 0.400-kg object undergoing SHM has ax = 1.80...Ch. 14 - On a frictionless, horizontal air track, a glider...Ch. 14 - A 0.500-kg mass on a spring has velocity as a...Ch. 14 - A 1.50-kg mass on a spring has displacement as a...Ch. 14 - BIO Weighing a Virus. In February 2004, scientists...Ch. 14 - CALC Jerk. A guitar string vibrates at a frequency...Ch. 14 - For the oscillating object in Fig. E14.4, what are...Ch. 14 - A small block is attached to an ideal spring and...Ch. 14 - A small block is attached to an ideal spring and...Ch. 14 - A 0.150-kg toy is undergoing SHM on the end of a...Ch. 14 - A harmonic oscillator has angular frequency and...Ch. 14 - A 0.500-kg glider, attached to the end of an ideal...Ch. 14 - A cheerleader waves her pom-pom in SHM with an...Ch. 14 - CP For the situation described in part (a) of...Ch. 14 - A block with mass m = 0.300 kg is attached to one...Ch. 14 - You are watching an object that is moving in SHM....Ch. 14 - A 2.00-kg frictionless block is attached to an...Ch. 14 - A 2.00-kg frictionless block attached to an ideal...Ch. 14 - A mass is oscillating with amplitude A at the end...Ch. 14 - A 175-g glider on a horizontal, frictionless air...Ch. 14 - A proud deep-sea fisherman hangs a 65.0-kg fish...Ch. 14 - A thrill-seeking cat with mass 4.00 kg is attached...Ch. 14 - A uniform, solid metal disk of mass 6.50 kg and...Ch. 14 - A certain alarm clock ticks four times each...Ch. 14 - A thin metal disk with mass 2.00 103 kg and...Ch. 14 - You want to find the moment of inertia of a...Ch. 14 - CALC The balance wheel of a watch vibrates with an...Ch. 14 - You pull a simple pendulum 0.240 m long to the...Ch. 14 - An 85.0-kg mountain climber plans to swing down,...Ch. 14 - A building in San Francisco has light fixtures...Ch. 14 - A Pendulum on Mars. A certain simple pendulum has...Ch. 14 - After landing on an unfamiliar planet, a space...Ch. 14 - In the laboratory, a student studies a pendulum by...Ch. 14 - A simple pendulum 2.00 m long swings through a...Ch. 14 - A small sphere with mass m is attached to a...Ch. 14 - Two pendulums have the same dimensions (length L)...Ch. 14 - We want to hang a thin hoop on a horizontal nail...Ch. 14 - A 1.80-kg connecting rod from a car engine is...Ch. 14 - Prob. 14.56ECh. 14 - The two pendulums shown in Fig. E14.57 each...Ch. 14 - CP A holiday ornament in the shape of a hollow...Ch. 14 - A 1.35-kg object is attached to a horizontal...Ch. 14 - A 50.0-g hard-boiled egg moves on the end of a...Ch. 14 - An unhappy 0.300-kg rodent, moving on the end of a...Ch. 14 - A mass is vibrating at the end of a spring of...Ch. 14 - A sinusoidally varying driving force is applied to...Ch. 14 - An object is undergoing SHM with period 0.300 s...Ch. 14 - An object is undergoing SHM with period 1.200 s...Ch. 14 - Four passengers with combined mass 250 kg compress...Ch. 14 - At the end of a ride at a winter-theme amusement...Ch. 14 - CP A block with mass M rests on a frictionless...Ch. 14 - A 1.50-kg, horizontal, uniform tray is attached to...Ch. 14 - CP A 10.0-kg mass is traveling to the right with a...Ch. 14 - An apple weighs 1.00 N. When you hang it from the...Ch. 14 - CP SHM of a Floating Object. An object with height...Ch. 14 - CP A square object of mass m is constructed of...Ch. 14 - An object with mass 0.200 kg is acted on by an...Ch. 14 - CALC A 2.00-kg bucket containing 10.0 kg of water...Ch. 14 - A uniform beam is suspended horizontally by two...Ch. 14 - A 5.00-kg partridge is suspended from a pear tree...Ch. 14 - A 0.0200-kg bolt moves with SHM that has an...Ch. 14 - CP SHM of a Butchers Scale. A spring of negligible...Ch. 14 - A 40.0-N force stretches a vertical spring 0.250...Ch. 14 - Dont Miss the Boat. While on a visit to Minnesota...Ch. 14 - CP An interesting, though highly impractical...Ch. 14 - CP A rifle bullet with mass 8.00 g and initial...Ch. 14 - CP Two uniform solid spheres, each with mass M =...Ch. 14 - CP In Fig. P14.85 the upper ball is released from...Ch. 14 - The Silently Ringing Bell. A large, 34.0-kg bell...Ch. 14 - CALC A slender, uniform, metal rod with mass M is...Ch. 14 - Two identical thin rods, each with mass m and...Ch. 14 - DATA A mass m is attached to a spring of force...Ch. 14 - DATA You hang various masses m from the end of a...Ch. 14 - DATA Experimenting with pendulums, you attach a...Ch. 14 - The Effective Force Constant of Two Springs. Two...Ch. 14 - CALC A Spring with Mass. The preceding problems in...Ch. 14 - BIO SEEING SURFACES AT THE NANOSCALE. One...Ch. 14 - In the model of Problem 14.94, what is the...Ch. 14 - By what percentage does the frequency of...
Additional Science Textbook Solutions
Find more solutions based on key concepts
3. What is free-fall, and why does it make you weightless? Briefly describe why astronauts are weightless in th...
The Cosmic Perspective
24. (Il) You buy a plastic dart gun, and being a clever physics student you decide to do a quick calculation to...
Physics: Principles with Applications
Write the abbreviation for each quantity.
23. 75 hectometres
Applied Physics (11th Edition)
What is the role of “loose” electrons in heat conductors?
Conceptual Physics (12th Edition)
A 12.00-V battery has an internal resistance of a tenth of an ohm. (a) What is the current if the battery termi...
University Physics Volume 2
52. You are target shooting using a toy gun that fires a small ball at a speed of 15 m/s. When the gun is fire...
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A horizontal, rigid bar of negligible weight is fixed against a vertical wall at one end and supported by a vertical string at the other end. The bar has a length of 50.0 cm and is used to support a hanging block of weight 400.0 N from a point 30.0 cm from the wall as shown in Figure P14.81. The string is made from a material with a tensile strength of 1.2 108 N/m2. Determine the largest diameter of the string for which it would still break. FIGURE P14.81arrow_forwardUse the data in Table P16.59 for a block of mass m = 0.250 kg and assume friction is negligible. a. Write an expression for the force FH exerted by the spring on the block. b. Sketch FH versus t.arrow_forwardA uniform wire (Y = 2.0 1011 N/m2) is subjected to a longitudinal tensile stress of 4.0 107 N/m2. What is the fractional change in the length of the wire?arrow_forward
- Consider a nanotube with a Youngs modulus of 2.130 1012 N/m2 that experiences a tensile stress of 5.3 1010 N/m2. Steel has a Youngs modulus of about 2.000 1011 Pa. How much stress would cause a piece of steel to experience the same strain as the nanotube?arrow_forwardA vibration sensor, used in testing a washing machine, consists of a cube of aluminum 1.50 cm on edge mounted on one end of a strip of spring steel (like a hacksaw blade) that lies in a vertical plane. The strips mass is small compared with that of the cube, but the strips length is large compared with the size of the cube. The other end of the strip is clamped to the frame of the washing machine that is not operating. A horizontal force of 1.43 N applied to the cube is required to hold it 2.75 cm away from its equilibrium position. If it is released, what is its frequency of vibration?arrow_forwardA lightweight spring with spring constant k = 225 N/m is attached to a block of mass m1 = 4.50 kg on a frictionless, horizontal table. The blockspring system is initially in the equilibrium configuration. A second block of mass m2 = 3.00 kg is then pushed against the first block, compressing the spring by x = 15.0 cm as in Figure P16.77A. When the force on the second block is removed, the spring pushes both blocks to the right. The block m2 loses contact with the springblock 1 system when the blocks reach the equilibrium configuration of the spring (Fig. P16.77B). a. What is the subsequent speed of block 2? b. Compare the speed of block 1 when it again passes through the equilibrium position with the speed of block 2 found in part (a). 77. (a) The energy of the system initially is entirely potential energy. E0=U0=12kymax2=12(225N/m)(0.150m)2=2.53J At the equilibrium position, the total energy is the total kinetic energy of both blocks: 12(m1+m2)v2=12(4.50kg+3.00kg)v2=(3.75kg)v2=2.53J Therefore, the speed of each block is v=2.53J3.75kg=0.822m/s (b) Once the second block loses contact, the first block is moving at the speed found in part (a) at the equilibrium position. The energy 01 this spring-block 1 system is conserved, so when it returns to the equilibrium position, it will be traveling at the same speed in the opposite direction, or v=0.822m/s. FIGURE P16.77arrow_forward
- A flexible chain weighing 40.0 N hangs between two hooks located at the same height (Fig. P12.9). At each hook, the tangent to the chain makes an angle = 42.0 with the horizontal. Find (a) the magnitude of the force each hook exerts on the chain and (b) the tension in the chain at its midpoint. Suggestion: For part (b), make a force diagram for half of the chain. Figure P12.9arrow_forwardA rod of length 4.00 m with negligible mass is hinged to a wall. A rope attached to the end of the rod runs up to the wall at an angle of exactly 45, helping support the rod, while a sign of weight 10.0 N is hanging by two ropes attached to the bottom of the rod. The ropes make an angle of exactly 30 with the rod as shown in Figure P14.79. Another sign with a weight of 10.0 N is attached to the top of the rod with its center of mass at the midpoint of the rod. The entire system is in equilibrium. Find the magnitude of the tension in the rope above the rod that is also attached to the wall. FIGURE P14.79 Problems 79 and 80.arrow_forwardUse the graph in Figure P14.46 to list the three materials from greatest Youngs modulus to smallest. Explain your reasoning. FIGURE P14.46arrow_forward
- The nuchal ligament in a horse supports the weight of the horse’s head. This ligament is much more elastic than a typical ligament, stretching from 15% to 45% longer than its resting length as a horse’s head moves up and down while it runs. This stretch of the ligament stores energy, making locomotion more efficient. Measurements on a segment of ligament show a linear stress-versusstrain relationship until the stress approaches 0.80. Smoothed data for the stretch are shown. The segment of ligament tested has a resting length of 40 mm. How long is the ligament at a strain of 0.60?A. 46 mmB. 52 mmC. 58 mmD. 64 mmarrow_forwardThe nuchal ligament in a horse supports the weight of the horse’s head. This ligament is much more elastic than a typical ligament, stretching from 15% to 45% longer than its resting length as a horse’s head moves up and down while it runs. This stretch of the ligament stores energy, making locomotion more efficient. Measurements on a segment of ligament show a linear stress-versusstrain relationship until the stress approaches 0.80. Smoothed data for the stretch are shown. What is the approximate Young’s modulus for the ligament?A. 4 x 105 N/m2B. 8 x 105 N/m2C. 3 x 106 N/m2D. 6 x 106 N/m2arrow_forwardThe nuchal ligament in a horse supports the weight of the horse’s head. This ligament is much more elastic than a typical ligament, stretching from 15% to 45% longer than its resting length as a horse’s head moves up and down while it runs. This stretch of the ligament stores energy, making locomotion more efficient. Measurements on a segment of ligament show a linear stress-versusstrain relationship until the stress approaches 0.80. Smoothed data for the stretch are shown. Suppose the ligament has a circular cross section. For a certain ligament, an investigator measures the restoring force at a strain of 0.40. If the ligament is replaced with one that has twice the diameter, by what factor does the restoring force increase?A. 1.4B. 2C. 4D. 8arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY