
Concept explainers
To calculate:
The probability that point chosen at the random lies in a shaded region:
Answer to Problem 31PPS
The probability of the point chosen at the random lies in a shaded region is
Explanation of Solution
Given information:
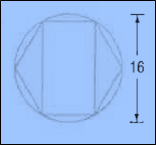
Calculation:
The figure consists of
Area of un-shaded rectangle:
The area of shaded hexagon is same to half of the perimeter of hexagon multiplied by the apothem of hexagon:
Then the area of un-shaded circle:
Area of un-shaded circle:
The probability that point chosen at the random lies in the shaded region dividing the area of shaded region by the area of the given figure:
The probability of the point chosen at the random lies in a shaded region is
Chapter 13 Solutions
Glencoe Geometry Student Edition C2014
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
University Calculus: Early Transcendentals (4th Edition)
Thinking Mathematically (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics (13th Edition)
- Can someone help me with this please?arrow_forwardMariela is in her classroom and looking out of a window at a tree, which is 20 feet away. Mariela’s line of sight to the top of the tree creates a 42° angle of elevation, and her line of sight to the base of the tree creates a 31° angle of depression. What is the height of the tree, rounded to the nearest foot? Be sure to show your work to explain how you got your answer.arrow_forward1arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

