
Concept explainers
To calculate:
The probability that point chosen at the random lies in shaded region:
Answer to Problem 29PPS
The probability of the point chosen at the random lies in shaded region is
Explanation of Solution
Given information:
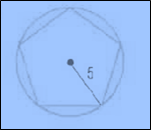
Calculation:
The given figure consists of shaded
The probability that the point chosen at random lies in shaded region is same to the area of shaded regions divided by the area of the given figure.
Let,
The area of pentagon is equal to half of apothem and the perimeter of the pentagon.
Since the
The area of pentagon:
The area of circle is given by
Where,
The area of circle:
The probability that point chosen at the random lies in shaded region by dividing the area of shaded region by the area of given figure:
The probability of the point chosen at the random lies in shaded region is
Chapter 13 Solutions
Glencoe Geometry Student Edition C2014
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
University Calculus: Early Transcendentals (4th Edition)
Calculus: Early Transcendentals (2nd Edition)
Algebra and Trigonometry (6th Edition)
Basic Business Statistics, Student Value Edition
Elementary Statistics: Picturing the World (7th Edition)
- Can someone help me with this please?arrow_forwardMariela is in her classroom and looking out of a window at a tree, which is 20 feet away. Mariela’s line of sight to the top of the tree creates a 42° angle of elevation, and her line of sight to the base of the tree creates a 31° angle of depression. What is the height of the tree, rounded to the nearest foot? Be sure to show your work to explain how you got your answer.arrow_forward1arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

