
Concept explainers
A spacecraft of mass m describes a circular orbit of radius r1 around the earth. (a) Show that the additional energy ΔE that must be imparted to the spacecraft to transfer it to a circular orbit of larger radius r2 is
where M is the mass of the earth. (b) Further show that if the transfer from one circular orbit to the other is executed by placing the spacecraft on a transitional semielliptic path AB, the amounts of energy ΔEA and ΔEB which must be imparted at A and B are, respectively, proportional to r2 and r1:
Fig. P13.116
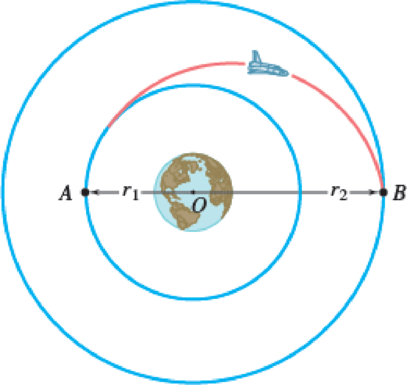
(a)
Show that additional energy
Answer to Problem 13.116P
The additional energy
Explanation of Solution
Given information:
The minimum distance between the center of the earth to the point A is
The maximum distance between the center of the earth to the point B is
The mass of the earth is M.
Calculation:
Show the figure with the force acting as in Figure (1).
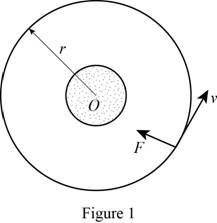
The expression for the normal acceleration
The expression for calculating the geocentric force acting on the spacecraft when it is on the surface of earth (F) as follows:
Here, G is the universal gravitational constant and M is the mass of the earth.
Calculate the velocity of the circular orbit (v) by considering the force equilibrium by taking Newton’s second law using the relation:
Substitute
The expression for the kinetic energy in the circular orbit (T) as follows;
The expression for the potential energy in the circular orbit (V) as follows;
Calculate the energy required (E) for the spacecraft using the relation:
Substitute
Substitute
The expression for the energy required for the circular orbit of radius
The expression for the energy required for the circular orbit of radius
Calculate the addition energy imparted to the spacecraft to transfer it to circular orbit
Substitute
Therefore, the additional energy
(b)
Show the transfer from one circular orbit to the other is executed by placing the spacecraft on transitional semi elliptic path AB, the amounts of energy
Answer to Problem 13.116P
The amount of energy imparted at A
Explanation of Solution
Given information:
The minimum distance between the center of the earth to the point A is
The maximum distance between the center of the earth to the point B is
The mass of the earth is M.
Calculation:
Consider the circular orbit of radius
The expression for the velocity of the circular orbit
Calculate the kinetic energy at the circular orbit
Substitute
Consider that the after the spacecraft engines are fired and it is placed on a semi-elliptic path AB.
The expression or the principle of conservation of angular momentum at point A to the point B as follows:
The expression for the kinetic energy at point B
Here, m is the mass of the satellite.
The expression for the gravitational potential energy at point B
The expression for the kinetic energy of the orbit at point A
The expression for the gravitational potential energy at point A
The expression for the principle of conservation of energy at the point A to point P as follows:
Substitute
Substitute
Simplify the Equation,
Substitute
Calculate the kinetic energy in the semi elliptic path AB
Substitute
Calculate the additional energy
Substitute
Divide and Multiply by
Substitute
Calculate the kinetic energy in the semi elliptic path AB
Substitute
Calculate the additional energy
Substitute
Divide and Multiply by
Substitute
Therefore, the amount of energy imparted at A
Want to see more full solutions like this?
Chapter 13 Solutions
VECTOR MECH...,STAT.+DYNA.(LL)-W/ACCESS
- The bevel gear shown in is subjected to the force F which is caused from contact with another gear. Part A F (201+8j 15k) N 40 mm Determine the moment of this force about the y axis of the gear shaft. Express your answer with the appropriate units. My = Value Submit Request Answer ? Units 30 mmarrow_forwardConsider the beam in. Part A 1.5 ft 200 lb 200lb 2 ft 30° 1.25 ft 30° If F 90 lb, determine the resultant couple moment. = Express your answer in pound-feet to three significant figures. Assume the positive direction is counterclockwise. ΑΣΦ vec MR = Submit Request Answer ? lb.ftarrow_forward4. An operating parameter often used by power plant engineers is the heat rate. The heat rate is defined as, HR Qbioler Wnet where Qbioler is the heat transfer rate (Btu/h) to the water in the boiler due to the combustion of a fuel and Wnet is the net power (kW) delivered by the plant. In comparison, the thermal efficiency of the power plant is defined as, nth Wnet Qbioler where the numerator and denominator have the same units. Consider a power plant that is delivering 1000 MW of power while utilizing a heat transfer rate of 3570 MW at the boiler. Determine the heat rate and thermal efficiency of this power plant.arrow_forward
- The shaft shown in the sketch is subjected to tensile torsional and bending loads Determine the principal stresses at the location of stress concentration ✓ D=45MR F=3MM 1000-M 1000N チ d=30mm 500N 150 мм MM- 120 MA-arrow_forwardcalculate moment of inertia of this tapered beam structurearrow_forwardThe system shown below is in statics equilibrium. Cable OB lies in the xy plane and makes a 30° angle with the positive x-axis. Cable OA lies along the negative y-axis. If the weight of the load being supported is 100 lb, determine the magnitude of the forces in all four cables: OA, OB, OC, and OD.arrow_forward
- This is a mechanics/statics problem involving finding internal reactions, V(x) and M(x). Please refer to image for details. I'm not sure about where to take cuts and how to formulate the equations as a function of x. For my support Reactions I got Ay = 1008.33 lb, By = 1416.67 lb and Cy = 175 lb. and for the first cut V(x) = 1008.33 -250(x) and M(x) = 1008.33x - 125x^2. I'm struggling with the equations for the 2nd and 3rd cut.arrow_forwardAs shown in the figure below, a ring is used to suspend a load and is supported by Cable OA and Spring OB. Given that the tension in Cable OA is 400 N, what is the weight of the load being supported? Assume the system is in static equilibrium.arrow_forward4. (a) State the conditions that must be met to ensure dynamic balance is achieved for long rotors. (b) A rotor carries three out-of-balance discs in planes A, B and C as shown in Figure 4. The out-of- balance mass x radius products of the rotor discs are tabulated in Table 4. The shaft is to be dynamically balanced by adding balancing masses in planes P and Q, spaced along the shaft at a distance da = 800 mm. Determine the magnitude mara and angular position of the balancing mass x radius product that must be added to plane Q. MBB Ов θε mdc Мага End View on Plane P P MBB MATA dA dB dc do Figure 4 moc Table 4 MATA = 0.6 kg mm 6A = 0° d₁ = 200 mm mers = 0.2 kg mm 6g = 45° dB = 400 mm mcrc = 0.4 kg mm Bc=240° dc = 600 mm Ans. (b) = 110.5°, moro = 0.2 kg mmarrow_forward
- Need help in adding demensioning am am so confusedarrow_forwardComplete the following activity. Save as .pdf and upload to the assignment to the dropbox. 口 Use the general dimensioning symbols to correctly specify the following requirements on the drawing above.arrow_forwardplease solve and show workarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





