
Concept explainers
A uniform disk of mass m = 10.0 kg and radius r = 34.0 cm mounted on a frictionless axle through its center, and initially at rest, is acted upon by two tangential forces of equal magnitude F, acting on opposite sides of its rim until a point on the rim experiences a centripetal acceleration of 4.00 m/s2 (Fig. P13.73). a. What is the
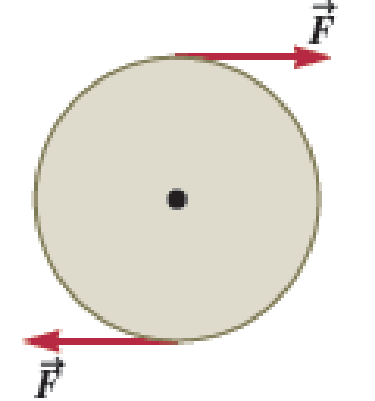
FIGURE P13.73
(a)
Angular momentum of the disk.
Answer to Problem 73PQ
Angular momentum of the disk is
Explanation of Solution
The disk in the question rotates about an axis passing through the center of the disk. Also the axis is perpendicular to the surface of the disk.
Write the equation to find the moment of inertia of the disk about an axis passing through its center.
Here,
Write the equation to find the centripetal acceleration felt by the disk.
Here,
Write the equation to find the linear speed.
Here,
Substitute equation (III) in (II).
Rewrite equation (IV) to get
Write the equation to find the angular momentum of the disk.
Here,
Substitute (V) to (VI) to get
Conclusion:
Substitute
Substitute
Therefore, angular momentum of the disk is
(b)
The time duration for which the force have to be applied so that the disk achieves the centripetal acceleration.
Answer to Problem 73PQ
The forces have to act for a time duration of
Explanation of Solution
Torque is the rate of change of angular momentum.
Write the equation to find the torque acting on the disk.
Here,
Rewrite equation (VIII) to get
Write the equation to find
Here,
Substitute above equation in (IX).
Change in angular momentum is the difference between the final angular momentum and initial angular momentum of the disk.
Rewrite equation (IX).
Here,
Conclusion:
The disk was initially at rest. Therefore
Substitute
Therefore, the forces have to act for a time duration of
Want to see more full solutions like this?
Chapter 13 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- No chatgpt pls will upvote Iarrow_forwardHow would partial obstruction of an air intake port of an air-entrainment mask effect FiO2 and flow?arrow_forward14 Z In figure, a closed surface with q=b= 0.4m/ C = 0.6m if the left edge of the closed surface at position X=a, if E is non-uniform and is given by € = (3 + 2x²) ŷ N/C, calculate the (3+2x²) net electric flux leaving the closed surface.arrow_forward
- No chatgpt pls will upvotearrow_forwardsuggest a reason ultrasound cleaning is better than cleaning by hand?arrow_forwardCheckpoint 4 The figure shows four orientations of an electric di- pole in an external electric field. Rank the orienta- tions according to (a) the magnitude of the torque on the dipole and (b) the potential energy of the di- pole, greatest first. (1) (2) E (4)arrow_forward
- What is integrated science. What is fractional distillation What is simple distillationarrow_forward19:39 · C Chegg 1 69% ✓ The compound beam is fixed at Ę and supported by rollers at A and B. There are pins at C and D. Take F=1700 lb. (Figure 1) Figure 800 lb ||-5- F 600 lb بتا D E C BO 10 ft 5 ft 4 ft-—— 6 ft — 5 ft- Solved Part A The compound beam is fixed at E and... Hình ảnh có thể có bản quyền. Tìm hiểu thêm Problem A-12 % Chia sẻ kip 800 lb Truy cập ) D Lưu of C 600 lb |-sa+ 10ft 5ft 4ft6ft D E 5 ft- Trying Cheaa Những kết quả này có hữu ích không? There are pins at C and D To F-1200 Egue!) Chegg Solved The compound b... Có Không ☑ ||| Chegg 10 וחarrow_forwardNo chatgpt pls will upvotearrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





