Chapter 13, Problem 52P

The hub diameter and projection for the gear of Prob. 13–51 are 100 and 37.5 mm, respectively. The face width of the gear is 50 mm. Locate bearings C and D on opposite sides, spacing C 10 mm from the gear on the hidden face (see figure) and D 10 mm from the hub face. Choose one as the thrust bearing, so that the axial load in the shaft is in compression. Find the output torque and the magnitudes and directions of the forces exerted by the bearings on the gearshaft.

To determine

The output torque.

The force exerted by the bearing $C$ on the gearshaft.

The force by the bearing $D$ on the gearshaft.

Answer to Problem 52P

The output torque is $979.75\text{N}\cdot \text{m}$.

The force exerted by the bearing $C$ on the gearshaft is $\left(231\text{N}\right)\widehat{j}+\left(3460\text{N}\right)\widehat{k}$.

The force by the bearing $D$ on the gearshaft is $-637\widehat{i}+1104.9\widehat{j}+1669.6\widehat{k}$.

Explanation of Solution

The figure below shows the forces acting at the centre of the gear $G$.

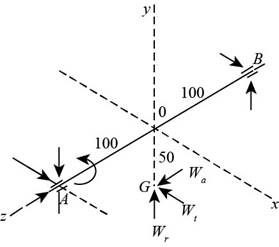
Figure-(1)

The tangential load on the centre of the gear is $W_t$, the radial load is $W_r$ and the axial load is $W_a$. The meshing point of gear and worm is O.

The figure below shows the forces on the bearing $C$ and $D$.

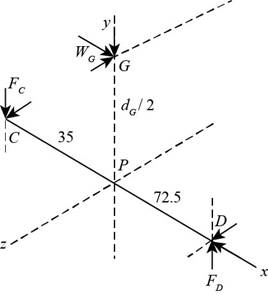
Figure-(2)

Write the expression for the linear velocity of the worm.

    $V_W=\frac{\pi dN}{60}$                                                                    (I)

Here, the pitch diameter of the worm is $d$ and the rotational speed of the gear is $N$.

Write the expression for the tangential load on the gear.

    $W_{Wt}=\frac{H}{V_W}$                                                            (II)

Here, the power is $H$.

Write the expression for lead.

    $L=p_t{N}_W$                                                                   (III)

Here, the number of threads on worm is $N_W$ and the tangential pitch is $p_t$.

Write the expression for the lead angle.

    $\lambda ={\tan }^{-1}\left(\frac{L}{\pi d}\right)$                                                                 (IV)

Write the expression for the force exerted by the by the gear on the worm.

    $W=\frac{W_{Wt}}{\cos {\varphi }_n\cdot \sin \lambda +f.\cos \lambda }$                                               (V)

Here, the normal pressure angle is ${\varphi }_n$ and the friction factor is $f$.

Write the expression for the sliding velocity.

    $V_s=\frac{V_W}{\cos \lambda }$                                                                 (VI)

Write the expression for the load in the y direction.

    $W^y=W\sin {\varphi }_n$                                                               (VII)

Write the expression for the load in the z direction.

    $W^z=W\left[\cos {\varphi }_n\cdot \cos \lambda -f\cdot \sin \lambda \right]$                                    (VIII)

Write the expression for vector form of the force against the worm.

    $\overrightarrow{W}=-W_{Wt}\widehat{i}+W^y\widehat{j}+W^z\widehat{k}$                                                  (IX)

The force on the gear will be equal but opposite to the force against the worm.

Write the expression for vector form of the force against the gear.

    ${\overrightarrow{W}}_G=-\left[\overrightarrow{W}\right]$                                                               (X)

Write the diameter of the gear.

    $d_G=\frac{N_G{p}_x}{\pi }$                                                                  (XI)

Here, the number of teeth on the gear is $N_G$ and the axial pitch is $p_x$.

The axial pitch and the transverse pitch is same hence $p_x=p_t$.

Write the position vector of $D$ with respect to $G$.

    ${\overrightarrow{R}}_{DG}=\left(PD\right)\left(-\widehat{i}\right)+\left(PG\right)\widehat{j}$                                       (XII)

Here, the distance between the points $P$ and $D$ is $PD$ and the distance between the points $P$ and $G$ is $PG$.

Write the position vector of $D$ with respect to $C$.

    ${\overrightarrow{R}}_{DC}=\left(DC\right)\left(-\widehat{i}\right)$                                                    (XIII)

Here, the distance between the points $D$ and $C$.

Write the moment equation at $D$.

    ${\overrightarrow{R}}_{DG}\times {\overrightarrow{W}}_G+{\overrightarrow{R}}_{DC}\times {\overrightarrow{F}}_C+\overrightarrow{T}=0$                                    (XIV)

Here, the force vector at $C$ is ${\overrightarrow{F}}_C$ and the torque is $\overrightarrow{T}$.

Write the expression for the force vector at $C$.

    ${\overrightarrow{F}}_C=F_C^x\widehat{i}+F_C^y\widehat{j}+F_C^z\widehat{k}$                                               (XV)

Here, the force in x-direction is $F_C^x$ and the force in the y direction is $F_C^y$.

Write the force balance equation for the bearing $D$.

    $\begin{array}{l}{\overrightarrow{F}}_D+{\overrightarrow{F}}_C+{\overrightarrow{W}}_G=0\\ {\overrightarrow{F}}_D=-\left({\overrightarrow{F}}_C+{\overrightarrow{W}}_G\right)\end{array}$                                                       (XVI)

Conclusion:

Substitute $100\text{mm}$ for $d$ and $600\text{rev}/\min$ for $N$ in Equation (I).

    $\begin{array}{c}{V}_W=\frac{\pi \left(100\text{mm}\right)\left(600\text{rev}/\min \right)}{60}\\ =\frac{\pi }{60}\times \left(100\text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\left(600\text{rev}/\min \right)\\ =\pi \text{m}/\text{s}\end{array}$

Substitute $2000\text{W}$ for $H$ and $\pi \text{m}/\text{s}$ for $V_W$ in Equation (II).

    $\begin{array}{c}{W}_{Wt}=\frac{2000\text{W}}{\pi \text{m}/\text{s}}\\ =636.619\frac{\text{W}}{\text{m}/\text{s}}\left(\frac{1\text{N}\cdot \text{m}/\text{s}}{1\text{W}}\right)\\ \approx 637\text{N}\end{array}$

Substitute $1$ for $N_W$ and $25\text{mm}$ for $p_t$ in Equation (III).

    $\begin{array}{c}L=\left(25\text{mm}\right)1\\ =25\text{mm}\end{array}$

Substitute $25\text{mm}$ for $L$ and $100\text{mm}$ for $d$ in the Equation (IV).

    $\begin{array}{c}\lambda ={\tan }^{-1}\left(\frac{25\text{mm}}{\pi \left(100\text{mm}\right)}\right)\\ ={\tan }^{-1}\left(\frac{1}{4\pi }\right)\\ ={\tan }^{-1}\left(1.2732\right)\\ \approx 4.55°\end{array}$

Substitute $\pi \text{m}/\text{s}$ for $V_W$ and $4.55°$ for $\lambda$ in Equation (VI).

    $\begin{array}{c}{V}_s=\frac{\pi \text{m}/\text{s}}{\cos 4.55°}\\ =\frac{\pi \text{m}/\text{s}}{0.9968}\\ =3.151\text{m}/\text{s}\end{array}$

Convert the units of sliding velocity from $\text{m}/\text{s}$ to $\text{ft}/\text{s}$.

    $\begin{array}{c}{V}_s=3.151\text{m}/\text{s}\left(\frac{3.28\text{ft}/\text{s}}{1\text{m}/\text{s}}\right)\left(\frac{60\text{s}}{1\text{min}}\right)\\ =10.3352\times 60\text{ft}/\text{min}\\ =620.1168\text{ft}/\min \\ \approx 620\text{ft}/\min \end{array}$

Refer to Figure 13-42 “Representative values of the coefficient of friction for worm gearing.” to obtain the friction coefficient as 0.043 with respect to sliding velocity as $620\text{ft}/\min$.

Substitute $0.043$ for $f$, $14.5°$ for ${\varphi }_n$, $4.55°$ for $\lambda$ and $637\text{N}$ for $W_{Wt}$ in Equation (V).

    $\begin{array}{c}W=\frac{637\text{N}}{\cos 14.5°\cdot \sin \left(4.55°\right)+\left(0.043\right)\cos \left(4.55°\right)}\\ =\frac{637\text{N}}{0.968\times 0.079+0.9968\times 0.043}\\ =\frac{637\text{N}}{0.1194}\\ \approx 5335\text{N}\end{array}$

Substitute $5335\text{N}$ for $W$ and $14.5°$ for ${\varphi }_n$ in the Equation (VII).

    $\begin{array}{c}{W}^y=\left(5335\text{N}\right)\sin \left(14.5°\right)\\ =\left(5335\text{N}\right)\times 0.2504\\ =1335.884\text{N}\\ \approx 1335.9\text{N}\end{array}$

Substitute $14.5°$ for ${\varphi }_n$, $4.55°$ for $\lambda$, $0.043$ for $f$ and $5335\text{N}$ for $W$ in Equation (VIII).

    $\begin{array}{c}{W}^z=5335\text{N}\left[\cos \left(14.5°\right)\cos \left(4.55°\right)-\left(0.043\right)\sin \left(4.55°\right)\right]\\ =5335\text{N}\left[0.968\times 0.9968-0.043\times 0.079\right]\\ =5335\text{N}\left[0.9615\right]\\ \approx 5129.6\text{N}\end{array}$

Substitute $5129.6\text{N}$ for $W^z$, $1335.9\text{N}$ for $W^y$ and $637\text{N}$ for $W_{Wt}$ in Equation (IX).

    $\begin{array}{c}\overrightarrow{W}=-\left(637\text{N}\right)\widehat{i}+\left(1335.9\text{N}\right)\widehat{j}+\left(5129.6\text{N}\right)\widehat{k}\\ =\left[-637\widehat{i}+1335.9\widehat{j}+5129.6\widehat{k}\right]\text{N}\end{array}$

Substitute $\left[-637\widehat{i}+1335.9\widehat{j}+5129.6\widehat{k}\right]\text{N}$ for $\overrightarrow{W}$ in Equation (X).

    $\begin{array}{c}{\overrightarrow{W}}_G=-\left[-637\widehat{i}+1335.9\widehat{j}+5129.6\widehat{k}\right]\text{N}\\ \text{=}\left[637\widehat{i}-1335.9\widehat{j}-5129.6\widehat{k}\right]\text{N}\end{array}$

Substitute $48$ for $N_G$ and $25\text{mm}$ for $p_x$ in the Equation (XI).

    $\begin{array}{c}{d}_G=\frac{\left(48\right)\left(25\text{mm}\right)}{\pi }\\ =\frac{1200\text{mm}}{\pi }\\ =381.97\text{mm}\\ \approx 382\text{mm}\end{array}$

Substitute $72.5\text{mm}$ for $PD$ and $191\text{mm}$ for $PG$ in the Equation (XII).

    $\begin{array}{c}{\overrightarrow{R}}_{DG}=\left(72.5\text{mm}\right)\left(-\widehat{i}\right)+\left(191\text{mm}\right)\widehat{j}\\ =\left(72.5\text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\left(-\widehat{i}\right)+\left(191\text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\widehat{j}\\ =-\left(0.0725\text{m}\right)\widehat{i}+\left(0.191\text{m}\right)\widehat{j}\end{array}$

Substitute $107.5\text{mm}$ for $DC$ in the Equation (XIII).

    $\begin{array}{c}{\overrightarrow{R}}_{DC}=\left(107.5\text{mm}\right)\left(-\widehat{i}\right)\\ =\left(107.5\text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\left(-\widehat{i}\right)\\ =-\left(0.1075\text{m}\right)\widehat{i}\end{array}$

Substitute $-\left(0.1075\text{m}\right)\widehat{i}$ for ${\overrightarrow{R}}_{DC}$, $-\left(0.0725\text{m}\right)\widehat{i}+\left(0.191\text{m}\right)\widehat{j}$ for ${\overrightarrow{R}}_{DG}$, $F_C^x\widehat{i}+F_C^y\widehat{j}+F_C^z\widehat{k}$ for ${\overrightarrow{F}}_C$ and $\left[637\widehat{i}-1335.9\widehat{j}-5129.6\widehat{k}\right]\text{N}$ for ${\overrightarrow{W}}_G$ in Equation (XIV).

    $\begin{array}{c}\left\{\begin{array}{l}\left[-\left(0.0725\text{m}\right)\widehat{i}+\left(0.191\text{m}\right)\widehat{j}\right]\times \left[\left(637\widehat{i}-1335.9\widehat{j}-5129.6\widehat{k}\right)\text{N}\right]\\ \text{+}\left[-\left(0.1075\text{m}\right)\widehat{i}\right]\times \left[F_C^x\widehat{i}+F_C^y\widehat{j}+F_C^z\widehat{k}\right]+T\widehat{i}\end{array}\right\}=0\\ \left[\begin{array}{l}96.852\widehat{k}-371.896\widehat{j}-121.667\widehat{k}-979.75\widehat{i}\\ -0.1075F_C^y\widehat{k}+0.1075F_C^z\widehat{j}+T\widehat{i}\end{array}\right]\text{N}\cdot \text{m}=0\\ \left[\begin{array}{l}\left(T-979.75\right)\widehat{i}+\left(0.1075F_C^z-371.896\right)\widehat{j}\\ +\left(96.852-121.667-0.1075F_C^y\right)\widehat{k}\end{array}\right]\text{N}\cdot \text{m}=0\\ \left[\begin{array}{l}\left(T-979.75\right)\widehat{i}+\left(0.1075F_C^z-371.896\right)\widehat{j}\\ +\left(-24.815-0.1075F_C^y\right)\widehat{k}\end{array}\right]\text{N}\cdot \text{m}=0\end{array}$    (XVII)

Solve Equation (XVII) for $\widehat{i}$.

    $\begin{array}{l}\left(T-979.75\right)\text{N}\cdot \text{m}=0\\ T=979.75\text{N}\cdot \text{m}\end{array}$

Thus, the output torque is $979.75\text{N}\cdot \text{m}$.

Solve Equation (XVII) for $\widehat{j}$.

    $\begin{array}{l}\left(0.1075F_C^z-371.896\right)\text{N}\cdot \text{m}\\ F_C^z=\frac{371.896\text{N}\cdot \text{m}}{0.1075\text{m}}\\ F_C^z=3459.49\text{N}\\ F_C^z\approx 3460\text{N}\end{array}$

Solve Equation (XVII) for $\widehat{k}$.

    $\begin{array}{l}\left(-24.815-0.1075F_C^y\right)\text{N}\cdot \text{m}=0\\ F_C^y=\frac{-24.815\text{N}\cdot \text{m}}{0.1075\text{m}}\\ F_C^y=230.83\text{N}\\ F_C^y\approx 231\text{N}\end{array}$

Substitute $0$ for $F_C^x$, $231\text{N}$ for $F_C^y$ and $3460\text{N}$ for $F_C^z$ in the Equation (XV).

    $\begin{array}{c}{\overrightarrow{F}}_C=0\widehat{i}+\left(231\text{N}\right)\widehat{j}+\left(3460\text{N}\right)\widehat{k}\\ =\left(231\text{N}\right)\widehat{j}+\left(3460\text{N}\right)\widehat{k}\end{array}$

Thus, the force exerted by the bearing $C$ on the gearshaft is $\left(231\text{N}\right)\widehat{j}+\left(3460\text{N}\right)\widehat{k}$.

Substitute $\left(231\text{N}\right)\widehat{j}+\left(3460\text{N}\right)\widehat{k}$ for ${\overrightarrow{F}}_C$ and $\left[637\widehat{i}-1335.9\widehat{j}-5129.6\widehat{k}\right]\text{N}$ for ${\overrightarrow{W}}_G$ in the Equation (XVI).

    $\begin{array}{c}{\overrightarrow{F}}_D=-\left\{\left(231\text{N}\right)\widehat{j}+\left(3460\text{N}\right)\widehat{k}+\left[637\widehat{i}-1335.9\widehat{j}-5129.6\widehat{k}\right]\text{N}\right\}\\ =-637\widehat{i}+1104.9\widehat{j}+1669.6\widehat{k}\end{array}$

Thus, the force by the bearing $D$ on the gearshaft is $-637\widehat{i}+1104.9\widehat{j}+1669.6\widehat{k}$.