
Interpretation:
The
Concept introduction:
The characters of the irreducible representations of the given point group can be multiplied by each other. The only condition is that the characters of the same symmetry operations are multiplied together. The multiplication of the characters is commutative.
The great orthogonality theorem for the reducible representation can be represented as,
Where,
•
•
•
•
•
Answer to Problem 13.84E
The
Explanation of Solution
The symmetry elements present in octahedral symmetry are,
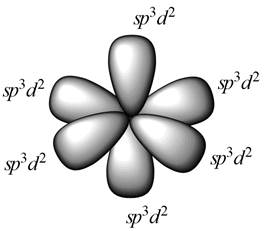
Figure 1
For the symmetry element
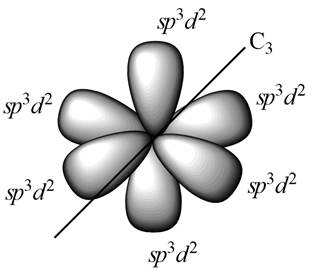
Figure 2
All the
For
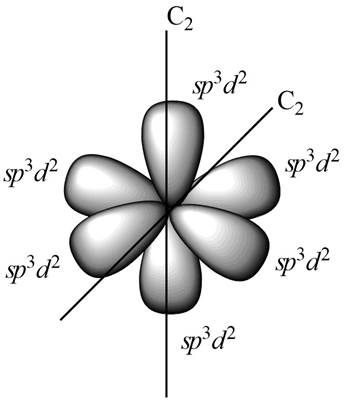
Figure 3
The
The
The
On inversion of the given set of orbitals, all the hybrid orbitals exchange their position and their contribution is
For
For
For
For
This plane can be represented as,
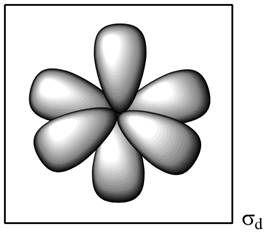
Figure 4
Thus, the reducible representations from the given contribution is,
The great orthogonality theorem for the reducible representation can be represented as,
Where,
•
•
•
•
•
The order of the group is
Substitute the value of order of the group, character of the class of the irreducible representation from character table of
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Similarly, for
The number of times the irreducible representation for
Thus, the linear combination is
The
Want to see more full solutions like this?
Chapter 13 Solutions
PHYSICAL CHEMISTRY-STUDENT SOLN.MAN.
- What is the approximate bond angle around the nitrogen atom? HNH H Harrow_forwardOH 1. NaOCH2CH3 Q 2. CH3CH2Br (1 equiv) H3O+ Select to Draw 1. NaOCH2 CH3 2. CH3Br (1 equiv) heat Select to Edit Select to Drawarrow_forwardComplete and balance the following half-reaction in acidic solution. Be sure to include the proper phases for all species within the reaction. S₂O₃²⁻(aq) → S₄O₆²⁻(aq)arrow_forward
- Q Select to Edit NH3 (CH3)2CHCI (1 equiv) AICI 3 Select to Draw cat. H2SO4 SO3 (1 equiv) HO SOCl2 pyridine Select to Edit >arrow_forwardComplete and balance the following half-reaction in basic solution. Be sure to include the proper phases for all species within the reaction. Zn(s) → Zn(OH)₄²⁻(aq)arrow_forwardb. ὋΗ CH3CH2OH H2SO4arrow_forward
- For the reaction A (g) → 3 B (g), Kp = 0.379 at 298 K. What is the value of ∆G for this reaction at 298 K when the partial pressures of A and B are 5.70 atm and 0.250 atm?arrow_forward14. Calculate the concentrations of Ag+, Ag(S2O3), and Ag(S2O3)23- in a solution prepared by mixing 150.0 mL of 1.00×10-3 M AgNO3 with 200.0 mL of 5.00 M Na2S2O3 Ag+ + S20 Ag(S203)¯ K₁ = 7.4 × 108 Ag(S203)¯ + S20¯ = Ag(S203) K₂ = 3.9 x 104arrow_forwardΗΝ, cyclohexanone pH 4-5 Draw Enamine I I CH3CH2Br THF, reflux H3O+ I Drawing Draw Iminium Ionarrow_forward
- :0: :0: Select to Add Arrows :0: (CH3)2NH :0: ■ Select to Add Arrows :0: :0: (CH3)2NH ■ Select to Add Arrowsarrow_forwardDraw the product of the following H action sequence. Ignore any inorganic byproducts formed. 1. (CH3CH2)2CuLi, THF 2. CH3Br Q Atoms, Bonds and Rings H Charges ㅁarrow_forwardPlease help me with this the problem is so confusingarrow_forward
 Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,





