
(a)
Interpretation:
The bubble point temperature for any one of the given binary systems in table
Concept Introduction:
Antoine equation is used to determine the vapor pressure of any substance at the given temperature by the equation:
Here,
Equation
to be used for Modified Raoult’s law is:
The Bubble point pressure for a binary system in vapor/liquid equilibrium is defined as the pressure where first bubble of vapor appears which is in equilibrium with the liquid present in the system. The equation which defines this pressure at this point is:
NRTL equations to be used are:
Here, the parameters
are calculated by the formula:
And,
are calculated by the formula:
Where,
(a)
Answer to Problem 13.50P
The bubble point temperature for
using NRTL equation is:
Explanation of Solution
Given information:
The pressure at which the bubble point temperature is to be calculated is
NRTL equation parameters are given in Table 13.10 as shown below:
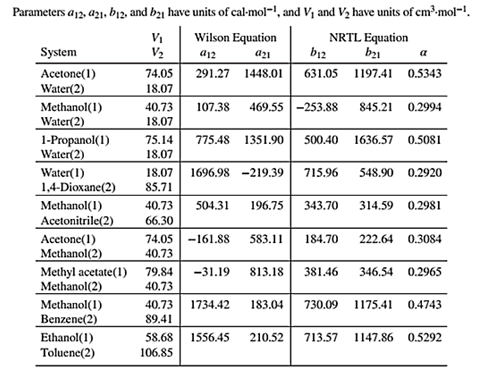
The binary system for which the bubble point temperature will be calculated is
. The liquid phase composition is:
From table B.2 of appendix B, the Antoine equation constants for
are:
Now, use equation (1) to calculate the vapor pressure of
as:
From table
to be used in NRTL equation are:
The value of universal gas constant to be used is,
Now, use equation (5) to calculate the values of
as:
Use equation (6) to calculate the values of
as:
Now, use these values of
using equations set (4) as:
Now, use the Modified Raoult’s law equation to calculate the pressure at the given value of
using the below mentioned formula as:
At
Make an initial guess for
using the preceding equations as:
(b)
Interpretation:
The dew point temperature for any one of the given binary systems in table
Concept Introduction:
Equation
to be used for Modified Raoult’s law is:
NRTL equations to be used are:
Here, the parameters
are calculated by the formula:
And,
are calculated by the formula:
Where,
The Dew point pressure for a binary system in vapor/liquid equilibrium is defined as the pressure where first drop of liquid appears which is in equilibrium with the vapor present in the system at a particular temperature. The equation that defines this pressure at this point is:
(b)
Answer to Problem 13.50P
The dew point temperature for
using NRTL equation is:
Explanation of Solution
Given information:
The pressure at which the bubble point temperature is to be calculated is
NRTL equation parameters are given in Table 13.10 as shown below:

Use the values of
as calculated in part (a) as:
The vapor phase composition is:
From table
to be used in NRTL equation are:
The value of universal gas constant to be used is,
Now, use equation (5) to calculate the values of
as:
Use equation (6) to calculate the values of
as:
Now, use these values of
using equations set (4) as:
Now, use the Modified Raoult’s law equation to calculate the pressure at the guessed value of
using the below mentioned formula as:
Make an initial guess for
as:
(c)
Interpretation:
Concept Introduction:
Equation
to be used for Modified Raoult’s law is:
The Bubble point pressure for a binary system in vapor/liquid equilibrium is defined as the pressure where first bubble of vapor appears which is in equilibrium with the liquid present in the system. The equation which defines this pressure at this point is:
The Dew point pressure for a binary system in vapor/liquid equilibrium is defined as the pressure where first drop of liquid appears which is in equilibrium with the vapor present in the system at a particular temperature. The equation that defines this pressure at this point is:
The equation for equilibrium ratio,
also known as K-value is:
Here,
The equations for flash calculations to be used are:
Here,
In terms of
is:
Here,
(c)
Answer to Problem 13.50P
The result of the
flash calculations is:
Explanation of Solution
Given information:
The flash pressure at which the
The condition for the flash temperature for this system is,
NRTL equation parameters are given in Table 13.10 as shown below:

Use the values of
as calculated in part (a) as:
To perform
To calculate bubble point temperature, let
Since, the given conditions are same as in part (a), the calculated value of
as in part (a) is:
To calculate dew point temperature, let
Since, the given conditions are same as in part (a), the calculated value of
as in part (a) is:
From the given condition of the flash temperature, it is calculated as:
Use this temperature to get the values of
as:
Now, calculate the values of
as:
Use equation (6) to calculate the values of
as:
Now, use these values of
using equations set (4) as:
Now, using the modified Raoult’s law, calculate the values of equilibrium ratio of component 1 and 2 using equations (2) and (8) as:
Now, use equation (10) and write it for both the component, 1 and 2 as shown below:
Since,
as:
Now, use equation (9) to calculate the value of
as:
Also, use the calculated value of
Using these values and the calculated values of
by equation (8) as:
Again, substitute these calculated values of
flash calculations are:
(d)
Interpretation:
The values of the azeotropic temperature and composition of the system is to be calculated if it exists for the given binary system.
Concept Introduction:
Antoine equation is used to determine the vapor pressure of any substance at the given temperature by the equation:
Here,
Equation
to be used for Modified Raoult’s law is:
NRTL equations to be used are:
Here, the parameters
are calculated by the formula:
And,
are calculated by the formula:
Where,
Relative volatility is defined by,
When
At the azeotropic point,
(d)
Answer to Problem 13.50P
The azeotropic values of temperature and composition for the binary system is calculated as:
Explanation of Solution
Given information:
The pressure at which the azeotrope of the system may exists is
NRTL equation parameters are given in Table 13.10 as shown below:

Use the given value of
as:
From table
to be used in NRTL equation are:
The value of universal gas constant to be used is,
Now, use equation (5) to calculate the values of
as:
Use equation (6) to calculate the values of
as:
Now, use these values of
Calculate
using equation (1) as:
Using equation (12) along with the modified Raoult’s law, calculate the value of relative volatility at
as:
For
using equations set (4) as:
Using equation (12) along with the modified Raoult’s law, calculate the value of relative volatility at
as:
Since
To calculate the azeotropic pressure, consider the condition
Consider the following set of equations in the given order as:
Now, use the values of
as:
Want to see more full solutions like this?
Chapter 13 Solutions
Introduction to Chemical Engineering Thermodynamics
- You are part of a team constructing a pipeline to transfer shale gas produced at the oceanfloor to the coastline. The temperature of the pipeline is nearly constant at 2 oC. The pipelineis made of smooth stainless steel and is 0.3 m in diameter and 100 m long. The averagevelocity of shale gas is 10 m/s and the inlet temperature is 20 oC ** Useful shale gas properties at 20 oC (Table A-12 for propane gas):(use these values for calculations and validate them later)• Density (ρ) = 18.13 kg/m3• Cp = 1974 J/kg-K• Viscosity (μ) = 8.54*10-6 kg/m-s• Pr = 0.918• k = 0.01836 W/m-Ka) Is the flow laminar or turbulent? Is the flow hydrodynamically and thermally fully developed?(circle your answer below and provide justification. • Laminar vs. Turbulent• Hydrodynamically developing vs. developed• Thermally developing vs. fully developedJustification: b) Calculate convective heat transfer coefficient (h). c) Calculate the exit temperature of the shale gas. d) Are the shale gas properties…arrow_forward3) A pilot-plant Podbielniak centrifugal extractor operating at 11,400 x g (this is G₁) is capable of processing 500 mL/min of filtered fermentation broth and 125 mL/min organic solvent, giving a recovery of 95%. The rotating cylinder inside the extractor has a diameter of 20 cm and is 2.5 cm wide. You need to scale up this extraction by using a larger Podbielniak extractor that has a diameter of 91 cm and width of 91 cm and delivers 2,300 x g (G2). What flow rates (in L/min) should be used in the larger extractor to achieve the same recovery efficiency?arrow_forward7) You are tasked with separating two proteins by ion exchange chromatography on a 30 cm long column with an inner diameter of 2 cm. The resin has a diameter of 100 μm and a void fraction of 0.3, and your mobile phase flows through the column at a rate of Q = 5 cm³/min. The Van Deemter coefficients A, B, and C have been determined to be 0.0228 cm, 0.0036 cm²/min, and 0.00053 min, respectively, for both proteins. Protein A elutes from the column with an average retention time of 27 min and standard deviation of 0.8 min. Protein B elutes from the column. with an average retention time of 33.8 min and standard deviation of 1.0. a) How many theoretical plates does the column contain? b) What flow rate (Q) will give you the maximum resolution? c) What is the minimum height of a theoretical plate for the system?arrow_forward
- 1 5) You are asked to design a moving bed adsorption process using two columns (see the figure below). Your feed contains 100 mg/L protein and flows through both columns at 4 m³/h. Fresh resin enters the bottom of both columns (resin does not flow from the bottom column to the top column). The maximum resin flow rate that your pumps can comfortably handle is 120 kg resin/h. Experimental data suggest that the adsorption equilibrium can be modeled as qi=4ci where qi is in g protein/kg resin and c; is in g protein/L broth. (Pay attention with units!) a) What is the lowest concentration of proteins that you could get in the effluent from column 1 (indicated by the *) in mg/L? (Hint: set up a mass balance) 0.25 , * 1 2 b) What should be the flow rate of resin (in kg/h) into the second column (B2) if your overall process needs to remove 99% of the protein?arrow_forward6) Instead of moving bed adsorption, you decide to try fixed bed adsorption with a different resin for removal of your protein. Your column is 25 cm long with an inner diameter of 5 cm. The resin packed in the column has a density of 1.5 g/cm³ and a void fraction of 0.25. Equilibrium data suggests that the protein binding to the column follows a Langmuir isotherm with an Stot = 6.25 g protein/kg resin and Keq = 2.58 L broth/g protein. The feed contains 100 mg/L protein and flows through the column at 500 mL/h. The calculated binding capacity of the column under these conditions is 945 mg protein. a) After 17.7 h, you detect an unacceptable level of protein in the column effluent. What is the length of unused bed? b) After deciding that this process will work well for separation, you need to scale up to a 1 m long column with the same diameter. If all else but length of the column is held constant, how long will you be able to run the column before breakthrough?arrow_forward2) A bioprocess stream contains two components: 60 g/L A (the desired bioproduct) and 40 g/L B (a contaminant). The partition coefficients in an extraction process are KA = 14.0 and KB = 0.5. If the stream is fed into a 5-stage countercurrent extractor at 25 L/min and solvent enters at 5 L/min, calculate the amount of each component in the extract phase at the outlet of the extractor.arrow_forward
- What flow rate (Q, in L/min) will give the maximum resolution if you scale up the process in problem 7 to a column with a diameter of 50 cm? (Use the conditions in the problem statement, not the optimal flow conditions calculated in the problem).arrow_forwardYou are asked to separate two proteins via size exclusion chromatography. Your column is 5 cm in diameter and 25 cm in length. You add 50 g (dry weight) of Sephacryl gel (density = 1.25 g/cm³) to the column. The volume outside of the gel and pores is 77 cm³. The column operates at a flow rate of 1 mL/min to not compress the resin. The average retention times of proteins A and B are 244.5 and 273 min, respectively. Under the given conditions, you calculate that there are 1600 theoretical plates in the column. (This problem continues onto the next page). a) What is the volume inside of the pores? b) What are the elution limits of this system (i.e., what re the minimum and maximum volumes that particles will elute in)? c) What are the gel partition coefficients of proteins A and B for this system? d) What are the peak widths for both proteins? e) Assuming the peak widths are 22 mL and 28 mL for proteins A and B, respectively (these values are not necessarily correct), what is the…arrow_forward1) Indicate whether each statement below is True or False: a) In extractions, small proteins usually end up in the heavy phase. b) In extractions, large proteins usually end up in the heavy phase. c) Tie line length on a phase diagram has no effect on protein partitioning. d) For extraction, we assume that each stage reaches equilibrium. e) Isotherms that are concave down lead to self-sharpening solute fronts in adsorption. f) When scaling up an adsorption unit, the LUB scales proportionally with adsorber length. g) For chromatography, separation efficiency increases when HETP increases. h) In size exclusion chromatography, smaller molecules elute from the column first. i) In hydrophobic interaction chromatography, very hydrophobic proteins elute in water. j) Molecules at very high concentrations elute from the column as a perfect Gaussian peak. k) In chromatography scale-up, resolution will increase as column diameter increases. 1) A good adsorbent typically has no porosity. m)…arrow_forward
- Chemical Engineering Use the psychrometric chart and demonstrate the linear interpolation method to obtain -0.52 KJ/KgDA. This is the enthalpy deviation. The exercise is uploaded below.arrow_forwardChemical Engineering Use the psychrometric chart. The remaining curves on the psychrometric chart are almost vertical and convex to the left, with labeled values (on Figure 8.4-1) of 0.05, 0.1, 0.2, and so on. (The units of these numbers arekJ/kg DA). Thesecurves are usedto determine theenthalpyof humid air that is not saturated. The procedure is as follows: (a) locate the point on the chart corresponding to air at its specified condition; (b) interpolate to estimate the enthalpy deviation at this point; (c) follow the constant wet-bulb temperature line to the enthalpy scale above the saturation curve, read the value on that scale, and add the enthalpy deviation to it. Also, you will see the exercise on the piece of paper.arrow_forwardCalculate the permeability of the bed of ion-exchange particles in Example 11.1.arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





