
(a)
Interpretation:
The parameter values for the Margules equation which provide the best fit of
Concept Introduction:
Equation
The formula to calculate the value of
Margules equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:
Here,
The equations used to calculate
(a)
Answer to Problem 13.32P
The parameter values for the Margules equation which provide the best fit of
The
Explanation of Solution
Given information:
The set of VLE data for the binary system containing methanol(1)/water(2) at
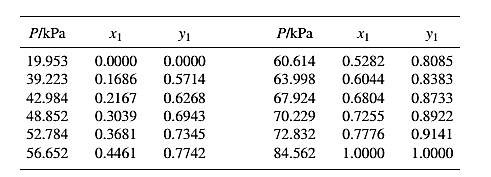
From the given data, first calculate the value of
Now, use equation (1) for the Modifies Raoult’s law and calculate the value of
Use the equation (2) to calculate the value of
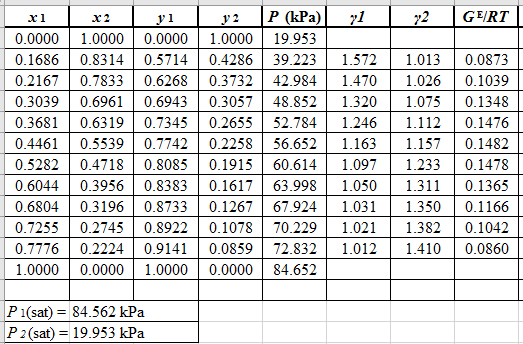
Rewrite equation (3) so that the equation becomes linear in
Now, calculate the values of
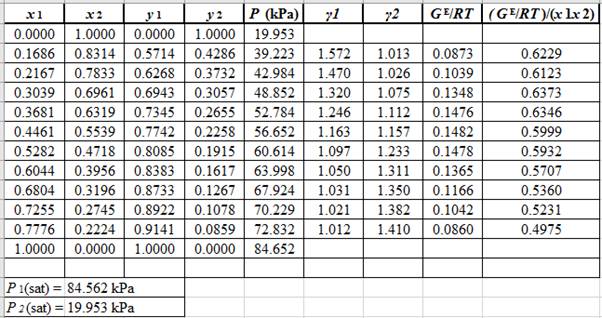
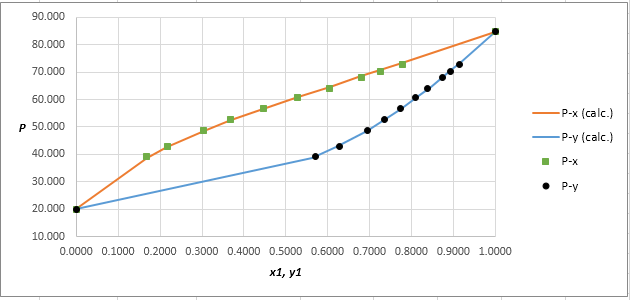
Plot the graph of
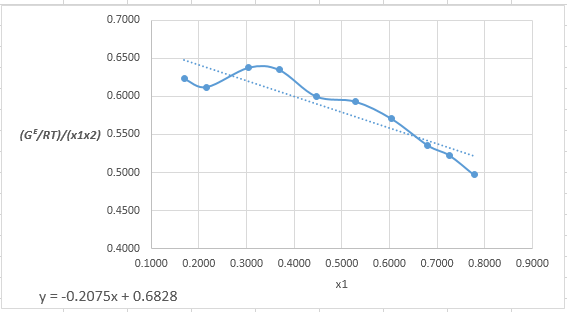
The equation that fits the plot is:
Compare it with equation (5) so that the values of
According to the above correlation for
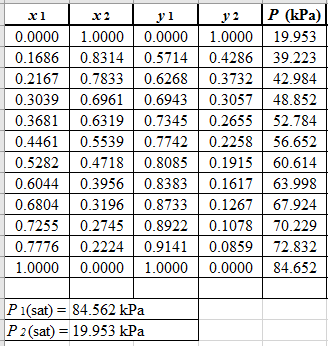
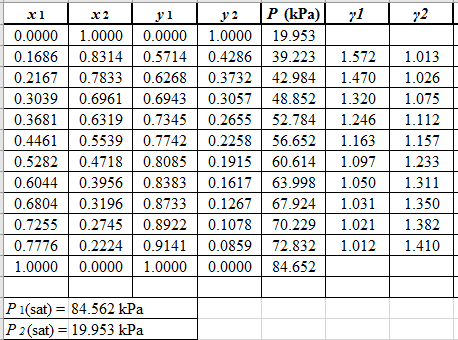
Now, using the above relations, calculate the values of
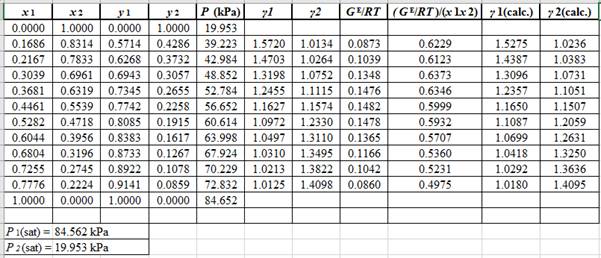
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of
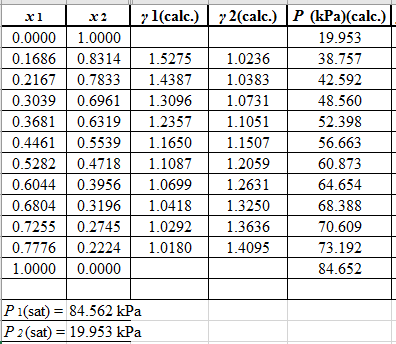
Now, use the below mentioned formula to calculate the value of
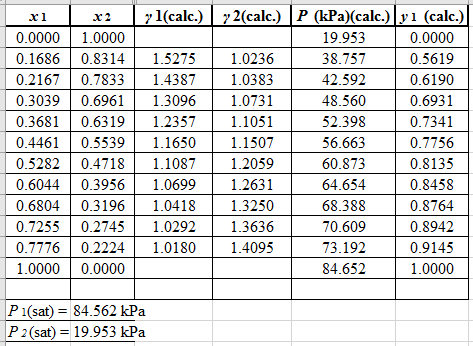
Using the tools of the excel, plot the graph of
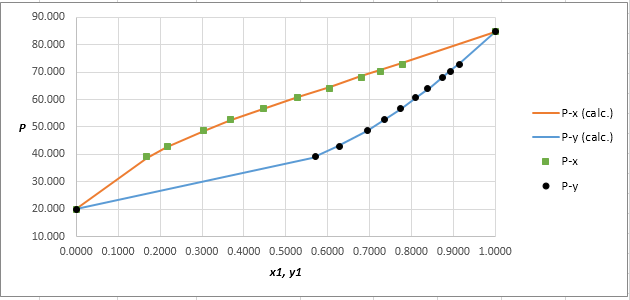
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:
Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.
(b)
Interpretation:
The parameter values for the van Laar equation which provide the best fit of
Concept Introduction:
Equation
The formula to calculate the value of
Van Laar equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:
Here,
The equations used to calculate
(b)
Answer to Problem 13.32P
The parameter values for the van Laar equation which provide the best fit of
The
Explanation of Solution
Given information:
The set of VLE data for the binary system containing methanol(1)/water(2) at
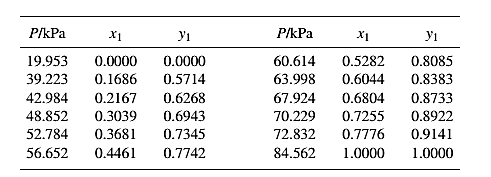
From the given data, first calculate the value of
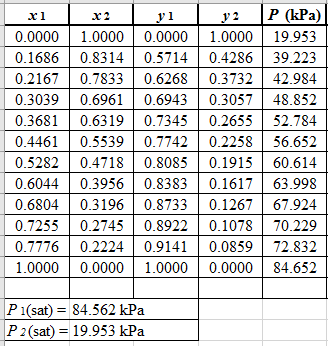
Now, use equation (1) for the Modifies Raoult’s law and calculate the value of
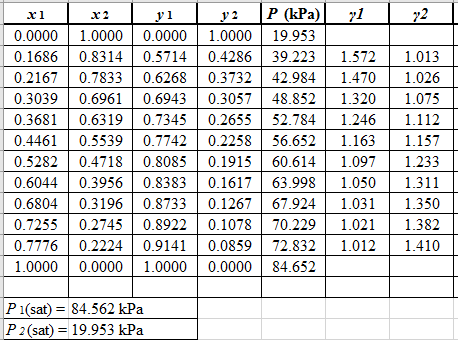
Use the equation (2) to calculate the value of
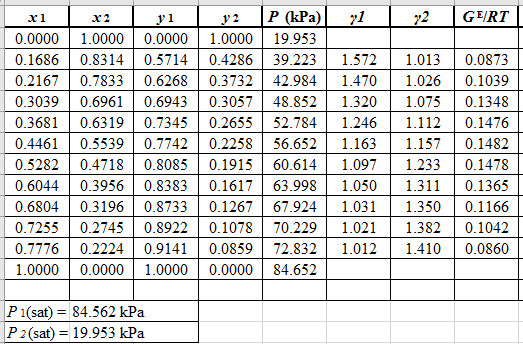
Rewrite equation (6) so that the equation becomes linear in
Now, calculate the values of
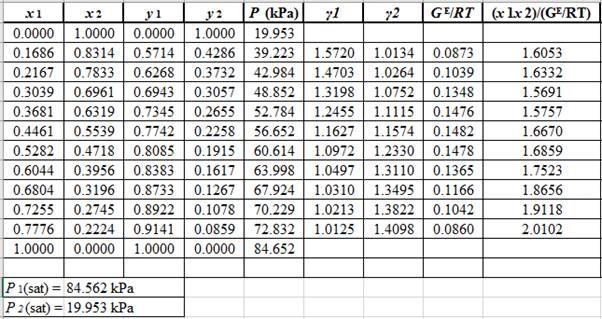
Plot the graph of
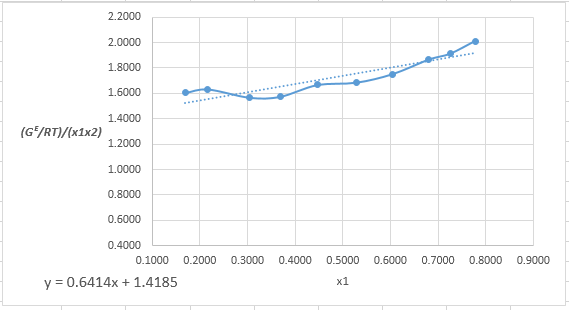
The equation that fits the plot is:
Compare it with equation (8) so that the values of
According to the above correlation for
Now, using the above relations, calculate the values of
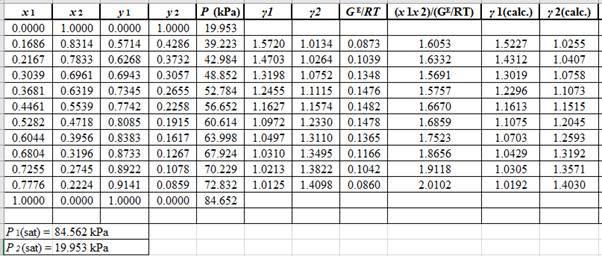
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of
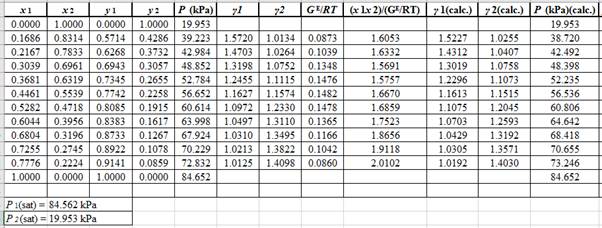
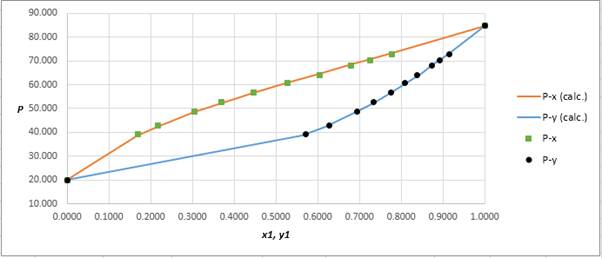
Now, use the below mentioned formula to calculate the value of
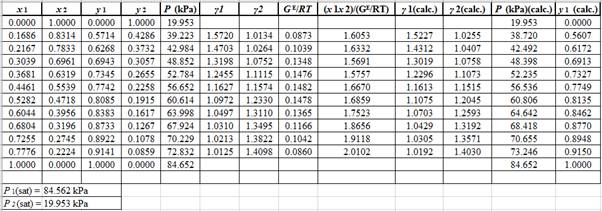
Using the tools of the excel, plot the graph of
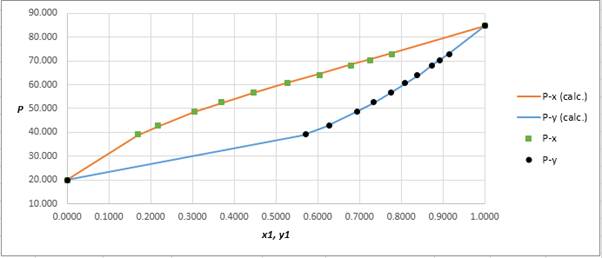
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:
Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.
(c)
Interpretation:
The parameter values for the Wilson equation which provide the best fit of
Concept Introduction:
Equation
The formula to calculate the value of
Wilson equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:
Here,
The equations used to calculate
(c)
Answer to Problem 13.32P
The parameter values for the Wilson equation which provide the best fit of
The
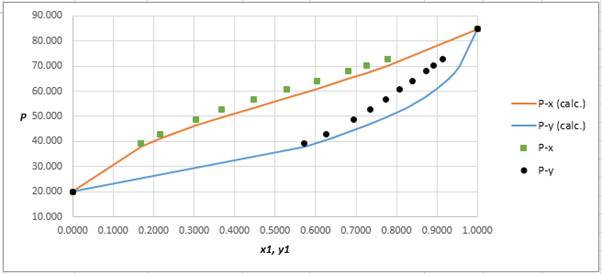
Explanation of Solution
Given information:
The set of VLE data for the binary system containing methanol(1)/water(2) at
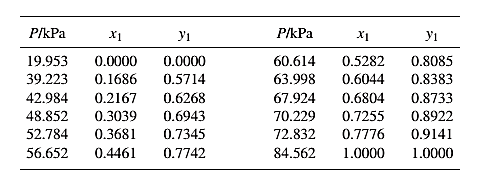
From the given data, first calculate the value of
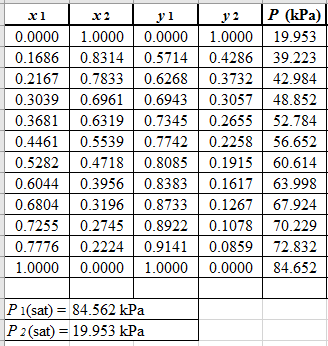
Now, use equation (1) for the Modifies Raoult’s law and calculate the value of
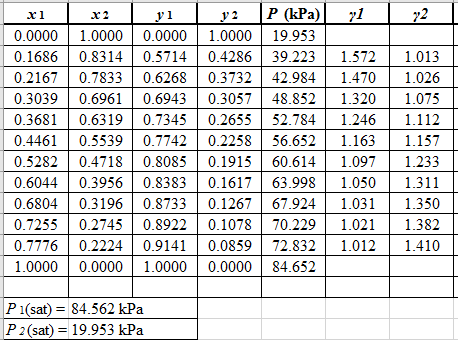
Use the equation (2) to calculate the value of
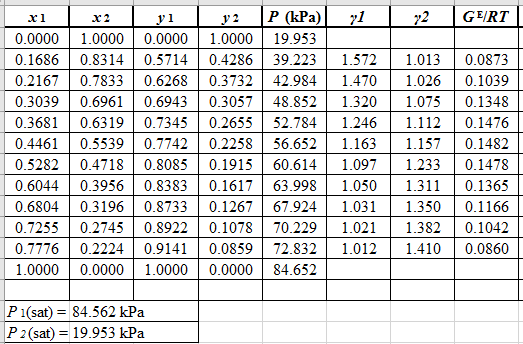
Now, use the method of the non-linear least square and fit the
Use the values of
Now, using the above relations, calculate the values of
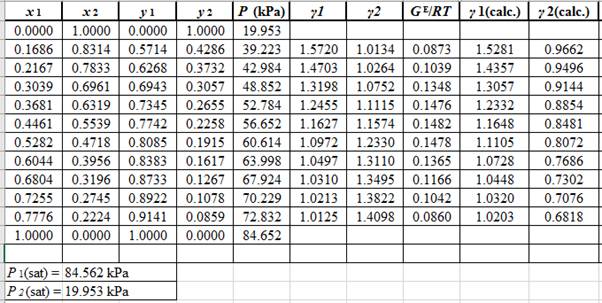
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of
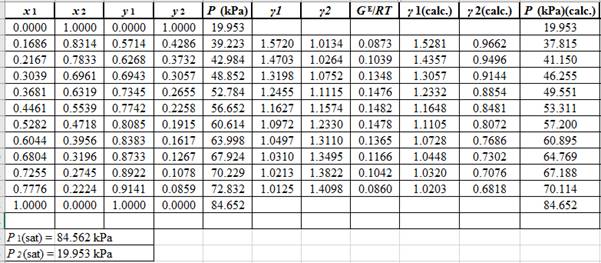
Now, use the below mentioned formula to calculate the value of
Using the tools of the excel, plot the graph of
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:
Since, the RMS value is considerable, the experimental and calculated value of pressure deviate from each other by a considerable measure.
(d)
Interpretation:
The parameter values for the Margules equation which provide the best fit of
Concept Introduction:
Equation
Margules equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:
Here,
The equations used to calculate
(d)
Answer to Problem 13.32P
The parameter values for the Margules equation which provide the best fit of
The plot residuals
Explanation of Solution
Given information:
The set of VLE data for the binary system containing methanol(1)/water(2) at
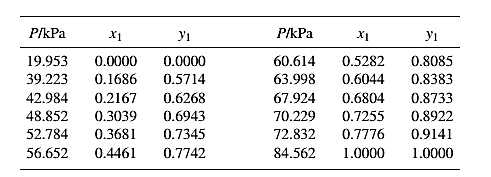
Barker’s Method is the method of determining the parameters by non-linear least squares.
Guess an initial value of
Now, calculate the value of
Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters
Using the equation set (4) and the parameter values, deduce the relation for
Now, using the above relations, calculate the values of
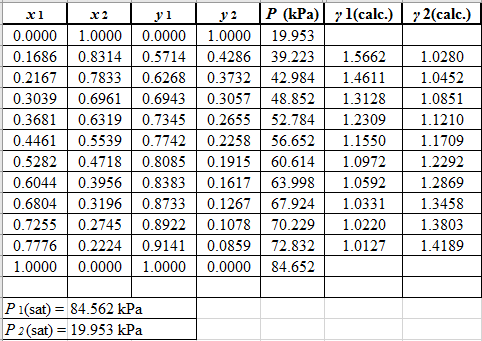
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of
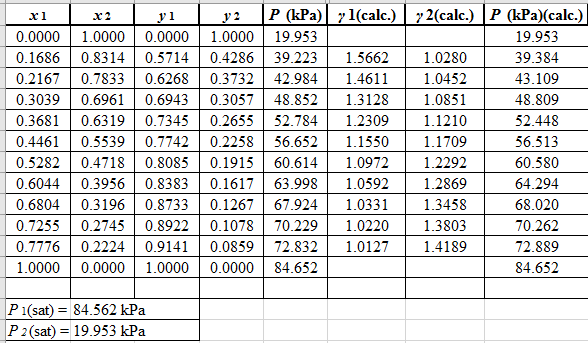
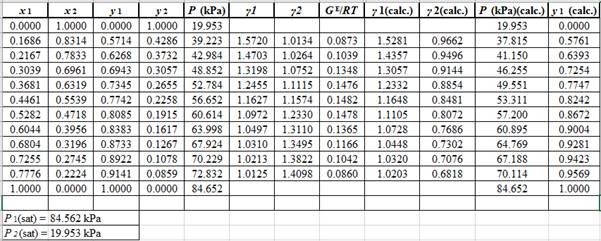
Now, use the below mentioned formula to calculate the value of
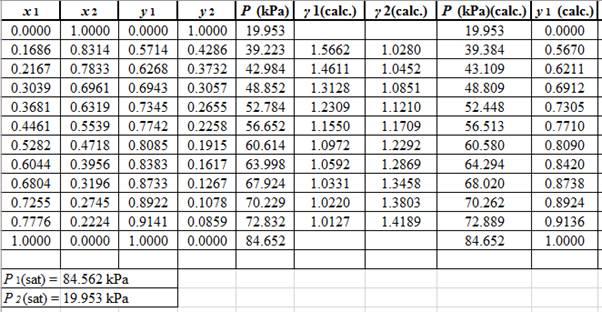
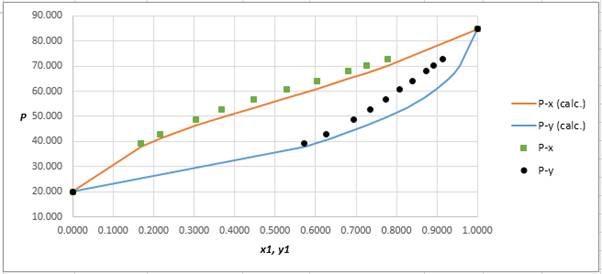
Using the tools of the excel, plot the graph of
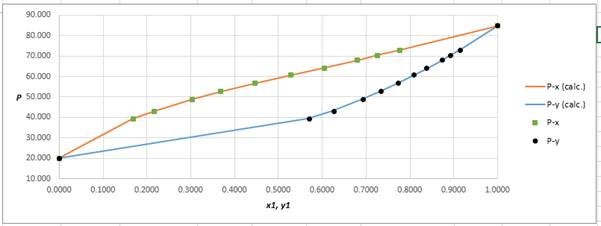
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:
Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.
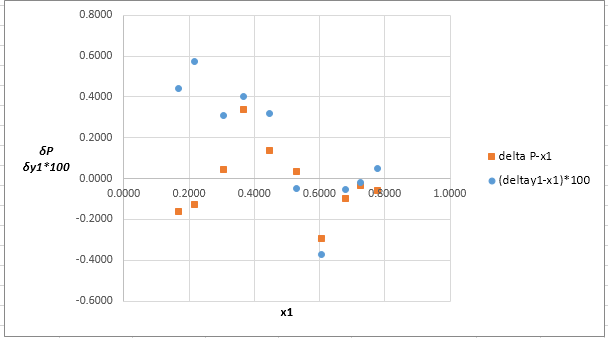
Now, calculate the residuals
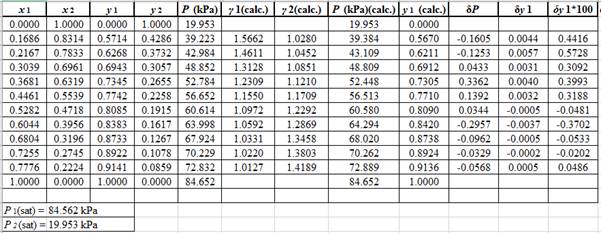
Plot these residuals against
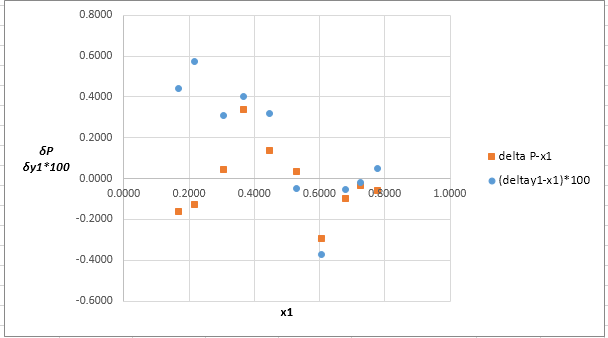
(e)
Interpretation:
The parameter values for the van Laar equation which provide the best fit of
Concept Introduction:
Equation
Van Laar equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:
Here,
The equations used to calculate
(e)
Answer to Problem 13.32P
The parameter values for the van Laar equation which provide the best fit of
The plot residuals
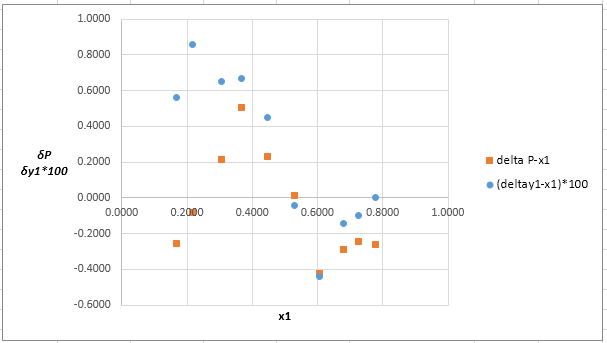
Explanation of Solution
Given information:
The set of VLE data for the binary system containing methanol(1)/water(2) at
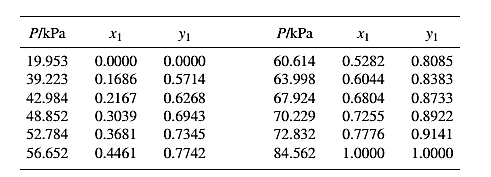
Barker’s Method is the method of determining the parameters by non-linear least squares.
Guess an initial value of
Now, calculate the value of
Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters
Using the equation set (7) and the parameter values, deduce the relation for
Now, using the above relations, calculate the values of
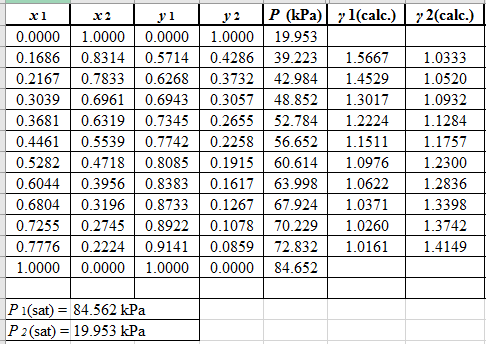
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of
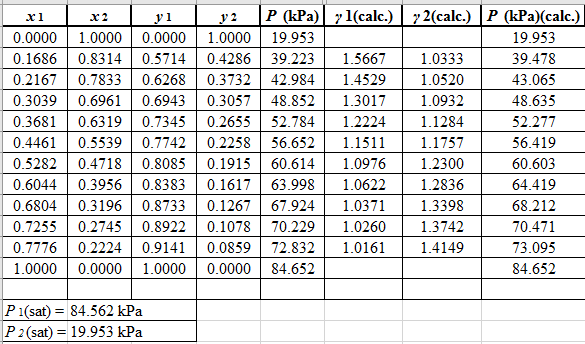
Now, use the below mentioned formula to calculate the value of
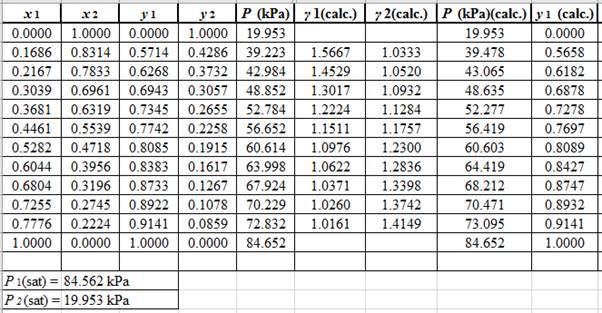
Using the tools of the excel, plot the graph of
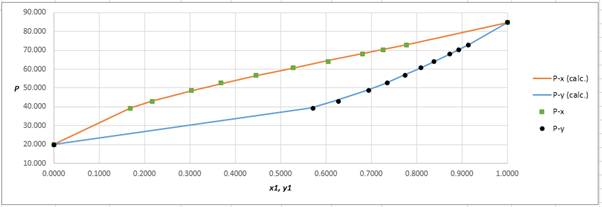
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:
Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.
Now, calculate the residuals
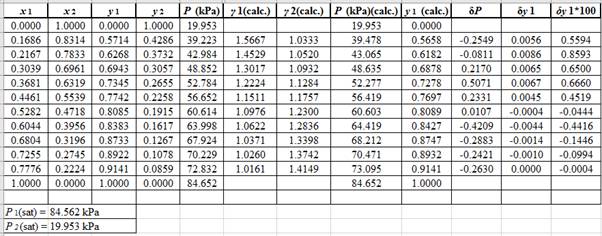
Plot these residuals against
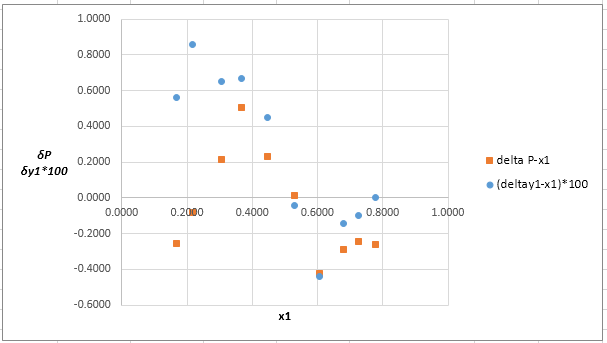
(f)
Interpretation:
The parameter values for the Wilson equation which provide the best fit of
Concept Introduction:
Equation
Wilson equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:
Here,
The equations used to calculate
(f)
Answer to Problem 13.32P
The parameter values for the Wilson equation which provide the best fit of
The plot residuals
Explanation of Solution
Given information:
The set of VLE data for the binary system containing methanol(1)/water(2) at
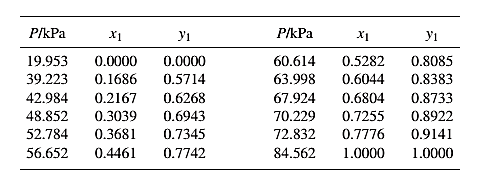
Barker’s Method is the method of determining the parameters by non-linear least squares.
Guess an initial value of
Now, calculate the value of
Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters
Using the equation set (10) and the parameter values, deduce the relation for
Now, using the above relations, calculate the values of
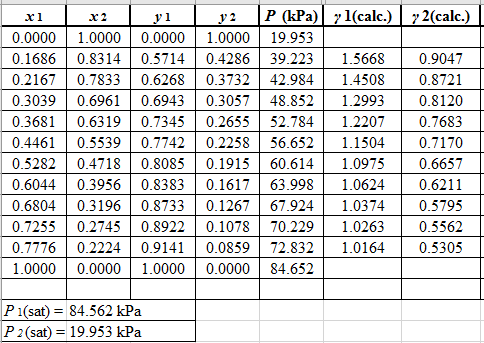
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of
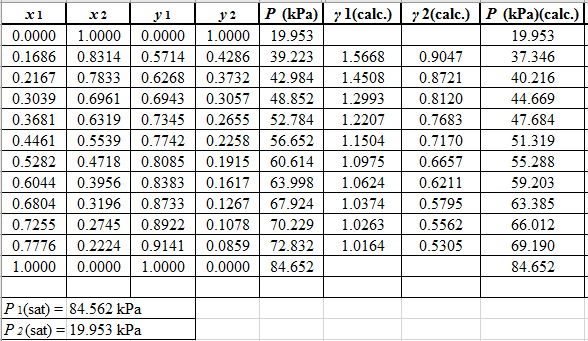
Now, use the below mentioned formula to calculate the value of
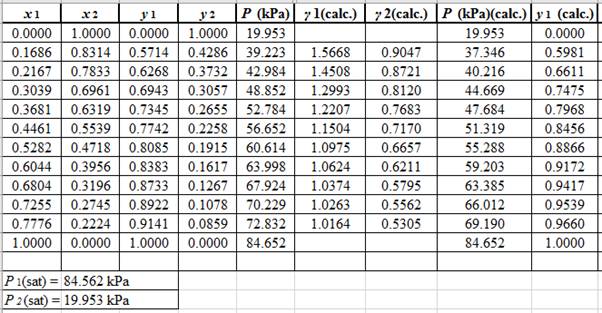
Using the tools of the excel, plot the graph of
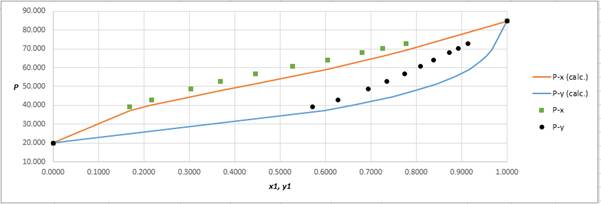
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:
Since, the RMS value is considerable, the experimental and calculated value of pressure deviate from each other by a considerable measure.
Now, calculate the residuals
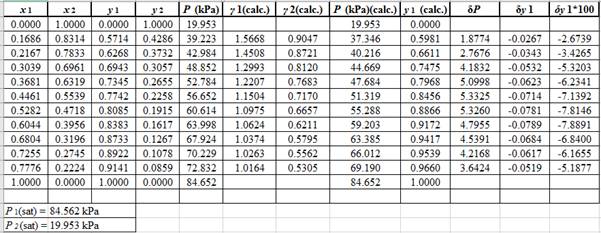
Plot these residuals against
Want to see more full solutions like this?
Chapter 13 Solutions
Introduction to Chemical Engineering Thermodynamics
- Untuk sistem gas etilena (1)/propilena (2), estimasi (f^1, f^2, $^1, dan ^2 pada t = 150°C, P = 30 bar, dan y1 = 0,35; kij = 0. (a) Dengan menerapkan Persamaan (10.63). (b) Dengan asumsi bahwa campuran adalah lingkungan idealarrow_forwardOnly focus on H(3), which is the specific enthalpy for nitrogen gas. chemical engineeringarrow_forwardchemical engineering. Only focus on H(3), which is the nitrogen gas. Start with the reference state to the process state. Be thorough to the fullestarrow_forward
- acetone with these parameters: po:=101325; #Standard atmospheric pressure in PaTfo:=273.15-94.45; #Melting temperature in K Tvo:=273.15+56.15; #Boiling temperature in K Hv:=31270; #Enthalpy of vaporization in J/molR:=8.314; #Gas Constant in J/mol*KNLe:=1.76; #Lewis number for acetoneMw:= 0.05808 ; #kg/mol molecular weight of acetoneW0:= 0.15; Wsp:=0.005;Am:= 0.12; #m^2/kg dry solid for the exposed wet areah:= 11; #W/m^2K for heat transfer coefficienttau__min:= Hv*(W0-Wsp)/Mw/Am/h/(T8-TS); tau__min/60;arrow_forwardchemical engineering Material-energy balance. Only focus on the nitrogen gas, which is H(3)arrow_forward1. The settling chamber, shown schematically in Figure 2E1.1, is used as a primary separation device in the removal of dust particles of density 1500 kg/m³ from a gas of density 0:7 kg/m³ and viscosity 1.90 x 10-5 Pa s. Gas inlet Elevation Gas Gas exit exit H Collection surface -W Section X-X Dimensions: H=3m L = 10 m W=2m Figure 2E1.1 Schematic diagram of settling chamber Assuming Stokes' law applies, show that the efficiency of collection of particles of size x is given by the expression collection efficiency, x = x²8(pp - Pi)L 18μHU where U is the uniform gas velocity through the parallel-sided section of the chamber. State any other assumptions made. (b) What is the upper limit of particle size for which Stokes' law applies? (c) When the volumetric flow rate of gas is 0.9 m³/s, and the dimensions of the chamber are those shown in Figure 2E1.1, determine the collection efficiency for spherical particles of diameter 30 mm.arrow_forward
- Can you answer this sequantially correct like show me the full process. Also, since it is chemical engineering related problem a perry's handbook is used. Thank youarrow_forwardchemical engineering Demonstrate how each specific enthalpy was calculated, from the reference state to the process state. Be thorough to the fullest. This is a material-energy balance. The answers are H(1) = 35.7 KJ/kmol, H(2) = 32.0 KJ/kmol, and H(3) = -1.26 KJ/kmol.arrow_forwardheat and mass transfer:arrow_forward
- Chemical Engineering. Be thorough to the fullest for the three enthalpies. H(1) = 35.7 kj/kmol H(2) =32.0 Kj/kmol H(3)= -1.26 Kj/kmolarrow_forwardchemical engineering Only solve the specific enthalpies. Be thorough to the fullest for each calculationarrow_forwardDo question 9 please! Question 7 Is just there for reference!!arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





