
McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Question
Chapter 12.1, Problem 2CE
To determine
To find: The number of lateral faces of the given prism.
Expert Solution & Answer
Answer to Problem 2CE
The number of lateral faces of the given prism is 6.
Explanation of Solution
Given information:
The right prism is given below:
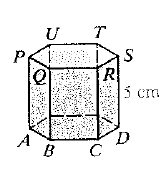
The faces of the prism that are not bases are lateral faces of the prism.
The total faces of the given prism are 8. The number of bases is 2.
So, the lateral faces of the prism are:
Therefore, the number of lateral faces of the given prism is 6.
Chapter 12 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 12.1 - Prob. 1CECh. 12.1 - Prob. 2CECh. 12.1 - Prob. 3CECh. 12.1 - Prob. 4CECh. 12.1 - Prob. 5CECh. 12.1 - Prob. 6CECh. 12.1 - Prob. 7CECh. 12.1 - Prob. 8CECh. 12.1 - Prob. 9CECh. 12.1 - Prob. 10CE
Ch. 12.1 - Prob. 1WECh. 12.1 - Prob. 2WECh. 12.1 - Prob. 3WECh. 12.1 - Prob. 4WECh. 12.1 - Prob. 5WECh. 12.1 - Prob. 6WECh. 12.1 - Prob. 7WECh. 12.1 - Prob. 8WECh. 12.1 - Prob. 9WECh. 12.1 - Prob. 10WECh. 12.1 - Prob. 11WECh. 12.1 - Prob. 12WECh. 12.1 - Prob. 13WECh. 12.1 - Prob. 14WECh. 12.1 - Prob. 15WECh. 12.1 - Prob. 16WECh. 12.1 - Prob. 17WECh. 12.1 - Prob. 18WECh. 12.1 - Prob. 19WECh. 12.1 - Prob. 20WECh. 12.1 - Prob. 21WECh. 12.1 - Prob. 22WECh. 12.1 - Prob. 23WECh. 12.1 - Prob. 24WECh. 12.1 - Prob. 25WECh. 12.1 - Prob. 26WECh. 12.1 - Prob. 27WECh. 12.1 - Prob. 28WECh. 12.1 - Prob. 29WECh. 12.1 - Prob. 30WECh. 12.1 - Prob. 31WECh. 12.1 - Prob. 32WECh. 12.1 - Prob. 33WECh. 12.1 - Prob. 34WECh. 12.1 - Prob. 35WECh. 12.1 - Prob. 36WECh. 12.1 - Prob. 37WECh. 12.1 - Prob. 38WECh. 12.1 - Prob. 39WECh. 12.1 - Prob. 40WECh. 12.1 - Prob. 1CCh. 12.1 - Prob. 2CCh. 12.1 - Prob. 3ECh. 12.2 - Prob. 1CECh. 12.2 - Prob. 2CECh. 12.2 - Prob. 3CECh. 12.2 - Prob. 4CECh. 12.2 - Prob. 5CECh. 12.2 - Prob. 6CECh. 12.2 - Prob. 7CECh. 12.2 - Prob. 8CECh. 12.2 - Prob. 9CECh. 12.2 - Prob. 10CECh. 12.2 - Prob. 11CECh. 12.2 - Prob. 12CECh. 12.2 - Prob. 13CECh. 12.2 - Prob. 14CECh. 12.2 - Prob. 15CECh. 12.2 - Prob. 16CECh. 12.2 - Prob. 17CECh. 12.2 - Prob. 18CECh. 12.2 - Prob. 1WECh. 12.2 - Prob. 2WECh. 12.2 - Prob. 3WECh. 12.2 - Prob. 4WECh. 12.2 - Prob. 5WECh. 12.2 - Prob. 6WECh. 12.2 - Prob. 7WECh. 12.2 - Prob. 8WECh. 12.2 - Prob. 9WECh. 12.2 - Prob. 10WECh. 12.2 - Prob. 11WECh. 12.2 - Prob. 12WECh. 12.2 - Prob. 13WECh. 12.2 - Prob. 14WECh. 12.2 - Prob. 15WECh. 12.2 - Prob. 16WECh. 12.2 - Prob. 17WECh. 12.2 - Prob. 18WECh. 12.2 - Prob. 19WECh. 12.2 - Prob. 20WECh. 12.2 - Prob. 21WECh. 12.2 - Prob. 22WECh. 12.2 - Prob. 23WECh. 12.2 - Prob. 24WECh. 12.2 - Prob. 25WECh. 12.2 - Prob. 26WECh. 12.2 - Prob. 27WECh. 12.2 - Prob. 28WECh. 12.2 - Prob. 29WECh. 12.2 - Prob. 30WECh. 12.2 - Prob. 31WECh. 12.2 - Prob. 32WECh. 12.2 - Prob. 1CCh. 12.2 - Prob. 2CCh. 12.2 - Prob. 3CCh. 12.2 - Prob. 4CCh. 12.2 - Prob. 1MRECh. 12.2 - Prob. 2MRECh. 12.2 - Prob. 3MRECh. 12.2 - Prob. 4MRECh. 12.2 - Prob. 5MRECh. 12.2 - Prob. 6MRECh. 12.2 - Prob. 7MRECh. 12.2 - Prob. 8MRECh. 12.2 - Prob. 9MRECh. 12.2 - Prob. 10MRECh. 12.3 - Prob. 1CECh. 12.3 - Prob. 2CECh. 12.3 - Prob. 3CECh. 12.3 - Prob. 4CECh. 12.3 - Prob. 5CECh. 12.3 - Prob. 6CECh. 12.3 - Prob. 7CECh. 12.3 - Prob. 8CECh. 12.3 - Prob. 1WECh. 12.3 - Prob. 2WECh. 12.3 - Prob. 3WECh. 12.3 - Prob. 4WECh. 12.3 - Prob. 5WECh. 12.3 - Prob. 6WECh. 12.3 - Prob. 7WECh. 12.3 - Prob. 8WECh. 12.3 - Prob. 9WECh. 12.3 - Prob. 10WECh. 12.3 - Prob. 11WECh. 12.3 - Prob. 12WECh. 12.3 - Prob. 13WECh. 12.3 - Prob. 14WECh. 12.3 - Prob. 15WECh. 12.3 - Prob. 16WECh. 12.3 - Prob. 17WECh. 12.3 - Prob. 18WECh. 12.3 - Prob. 19WECh. 12.3 - Prob. 20WECh. 12.3 - Prob. 21WECh. 12.3 - Prob. 22WECh. 12.3 - Prob. 23WECh. 12.3 - Prob. 24WECh. 12.3 - Prob. 25WECh. 12.3 - Prob. 26WECh. 12.3 - Prob. 27WECh. 12.3 - Prob. 28WECh. 12.3 - Prob. 29WECh. 12.3 - Prob. 30WECh. 12.3 - Prob. 31WECh. 12.3 - Prob. 32WECh. 12.3 - Prob. 33WECh. 12.3 - Prob. 34WECh. 12.3 - Prob. 35WECh. 12.3 - Prob. 36WECh. 12.3 - Prob. 37WECh. 12.3 - Prob. 38WECh. 12.3 - Prob. 39WECh. 12.3 - Prob. 40WECh. 12.3 - Prob. 1CCh. 12.3 - Prob. 1ST1Ch. 12.3 - Prob. 2ST1Ch. 12.3 - Prob. 3ST1Ch. 12.3 - Prob. 4ST1Ch. 12.3 - Prob. 5ST1Ch. 12.3 - Prob. 6ST1Ch. 12.3 - Prob. 7ST1Ch. 12.3 - Prob. 8ST1Ch. 12.3 - Prob. 1CKCh. 12.3 - Prob. 2CKCh. 12.3 - Prob. 3CKCh. 12.3 - Prob. 4CKCh. 12.4 - Prob. 1CECh. 12.4 - Prob. 2CECh. 12.4 - Prob. 3CECh. 12.4 - Prob. 4CECh. 12.4 - Prob. 5CECh. 12.4 - Prob. 6CECh. 12.4 - Prob. 7CECh. 12.4 - Prob. 8CECh. 12.4 - Prob. 9CECh. 12.4 - Prob. 1WECh. 12.4 - Prob. 2WECh. 12.4 - Prob. 3WECh. 12.4 - Prob. 4WECh. 12.4 - Prob. 5WECh. 12.4 - Prob. 6WECh. 12.4 - Prob. 7WECh. 12.4 - Prob. 8WECh. 12.4 - Prob. 9WECh. 12.4 - Prob. 10WECh. 12.4 - Prob. 11WECh. 12.4 - Prob. 12WECh. 12.4 - Prob. 13WECh. 12.4 - Prob. 14WECh. 12.4 - Prob. 15WECh. 12.4 - Prob. 16WECh. 12.4 - Prob. 17WECh. 12.4 - Prob. 18WECh. 12.4 - Prob. 19WECh. 12.4 - Prob. 20WECh. 12.4 - Prob. 21WECh. 12.4 - Prob. 22WECh. 12.4 - Prob. 23WECh. 12.4 - Prob. 24WECh. 12.4 - Prob. 25WECh. 12.4 - Prob. 26WECh. 12.4 - Prob. 27WECh. 12.4 - Prob. 28WECh. 12.4 - Prob. 29WECh. 12.4 - Prob. 30WECh. 12.4 - Prob. 31WECh. 12.4 - Prob. 32WECh. 12.4 - Prob. 33WECh. 12.4 - Prob. 34WECh. 12.4 - Prob. 1CCh. 12.4 - Prob. 1CKCh. 12.4 - Prob. 2CKCh. 12.4 - Prob. 3CKCh. 12.4 - Prob. 4CKCh. 12.4 - Prob. 1AECh. 12.4 - Prob. 2AECh. 12.4 - Prob. 1BECh. 12.4 - Prob. 2BECh. 12.4 - Prob. 3BECh. 12.4 - Prob. 1MRECh. 12.4 - Prob. 2MRECh. 12.4 - Prob. 3MRECh. 12.4 - Prob. 4MRECh. 12.4 - Prob. 5MRECh. 12.4 - Prob. 6MRECh. 12.5 - Prob. 1CECh. 12.5 - Prob. 2CECh. 12.5 - Prob. 3CECh. 12.5 - Prob. 4CECh. 12.5 - Prob. 5CECh. 12.5 - Prob. 6CECh. 12.5 - Prob. 7CECh. 12.5 - Prob. 8CECh. 12.5 - Prob. 9CECh. 12.5 - Prob. 10CECh. 12.5 - Prob. 11CECh. 12.5 - Prob. 12CECh. 12.5 - Prob. 13CECh. 12.5 - Prob. 1WECh. 12.5 - Prob. 2WECh. 12.5 - Prob. 3WECh. 12.5 - Prob. 4WECh. 12.5 - Prob. 5WECh. 12.5 - Prob. 6WECh. 12.5 - Prob. 7WECh. 12.5 - Prob. 8WECh. 12.5 - Prob. 9WECh. 12.5 - Prob. 10WECh. 12.5 - Prob. 11WECh. 12.5 - Prob. 12WECh. 12.5 - Prob. 13WECh. 12.5 - Prob. 14WECh. 12.5 - Prob. 15WECh. 12.5 - Prob. 16WECh. 12.5 - Prob. 17WECh. 12.5 - Prob. 18WECh. 12.5 - Prob. 19WECh. 12.5 - Prob. 20WECh. 12.5 - Prob. 21WECh. 12.5 - Prob. 22WECh. 12.5 - Prob. 23WECh. 12.5 - Prob. 24WECh. 12.5 - Prob. 25WECh. 12.5 - Prob. 26WECh. 12.5 - Prob. 27WECh. 12.5 - Prob. 28WECh. 12.5 - Prob. 29WECh. 12.5 - Prob. 1ST2Ch. 12.5 - Prob. 2ST2Ch. 12.5 - Prob. 3ST2Ch. 12.5 - Prob. 4ST2Ch. 12.5 - Prob. 5ST2Ch. 12.5 - Prob. 6ST2Ch. 12.5 - Prob. 1CKCh. 12.5 - Prob. 2CKCh. 12.5 - Prob. 3CKCh. 12.5 - Prob. 4CKCh. 12.5 - Prob. 5CKCh. 12.5 - Prob. 6CKCh. 12.5 - Prob. 1AECh. 12.5 - Prob. 2AECh. 12.5 - Prob. 1BECh. 12 - Prob. 1ECh. 12 - Prob. 2ECh. 12 - Prob. 3ECh. 12 - Prob. 4ECh. 12 - Prob. 5ECh. 12 - Prob. 6ECh. 12 - Prob. 1CRCh. 12 - Prob. 2CRCh. 12 - Prob. 3CRCh. 12 - Prob. 4CRCh. 12 - Prob. 5CRCh. 12 - Prob. 6CRCh. 12 - Prob. 7CRCh. 12 - Prob. 8CRCh. 12 - Prob. 9CRCh. 12 - Prob. 10CRCh. 12 - Prob. 11CRCh. 12 - Prob. 12CRCh. 12 - Prob. 13CRCh. 12 - Prob. 14CRCh. 12 - Prob. 15CRCh. 12 - Prob. 16CRCh. 12 - Prob. 17CRCh. 12 - Prob. 18CRCh. 12 - Prob. 19CRCh. 12 - Prob. 1CTCh. 12 - Prob. 2CTCh. 12 - Prob. 3CTCh. 12 - Prob. 4CTCh. 12 - Prob. 5CTCh. 12 - Prob. 6CTCh. 12 - Prob. 7CTCh. 12 - Prob. 8CTCh. 12 - Prob. 9CTCh. 12 - Prob. 10CTCh. 12 - Prob. 11CTCh. 12 - Prob. 12CTCh. 12 - Prob. 13CTCh. 12 - Prob. 14CTCh. 12 - Prob. 15CTCh. 12 - Prob. 16CTCh. 12 - Prob. 1CURCh. 12 - Prob. 2CURCh. 12 - Prob. 3CURCh. 12 - Prob. 4CURCh. 12 - Prob. 5CURCh. 12 - Prob. 6CURCh. 12 - Prob. 7CURCh. 12 - Prob. 8CURCh. 12 - Prob. 9CURCh. 12 - Prob. 10CURCh. 12 - Prob. 11CURCh. 12 - Prob. 12CURCh. 12 - Prob. 13CURCh. 12 - Prob. 14CURCh. 12 - Prob. 15CURCh. 12 - Prob. 16CURCh. 12 - Prob. 17CURCh. 12 - Prob. 18CURCh. 12 - Prob. 19CURCh. 12 - Prob. 20CUR
Additional Math Textbook Solutions
Find more solutions based on key concepts
Evaluate the integrals in Exercises 1–14.
3.
University Calculus: Early Transcendentals (4th Edition)
1. Drone Deliveries Based on a Pitney Bowes survey, assume that 42% of consumers are comfortable having drones ...
Elementary Statistics (13th Edition)
In Exercises 5-36, express all probabilities as fractions.
23. Combination Lock The typical combination lock us...
Elementary Statistics
A child has 12 blocks, of which 6 are black, 4 are red, 1 is white, and 1 is blue. If the child puts the blocks...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- If AB = 10 and AC = 13, what is AD? B A D C Write your answer as a whole number or as a decimal rounded to the nearest hundredth.arrow_forwardHeight = 1 Width=1 How much is the shaded area in the chart above?arrow_forwardLauris Online Back to Subject 不 4 ப 12 2 points T 35° 25° R M 4 N P 6Q 5 What is m/MNT? 120 T 12 What is the length of MR? 120 units 167:02:04 Time Remaining Yama is designing a company logo. The company president requested for the logo to be made of triangles. Yama is proposing the design shown. C 64°F Clear Q Search L 13 Ide dia des You scre Edi 12 L Tarrow_forward
- Classwork for Geometry 1st X S Savvas Realize * MARYIA DASHUTSINA-Ba → CA savvasrealize.com/dashboard/classes/49ec9fc00d8f48ec9a4b05b30c9ee0ba A > SIS © = =Wauconda Middle S... 31 WMS 8th Grade Tea... SIS Grades and Attenda.... esc GEOMETRY 1ST < Study Guide T6 K 18 L 63° 9 N M Quadrilateral JKLM is a parallelogram. What is the m ZKJN? mZKJN = Review Progress acerarrow_forwardWhy is this proof incorrect? State what statement and/or reason is incorrect and why. Given: Overline OR is congruent to overline OQ, angle N is congruent to angle PProve: Angle 3 is congruent to angle 5 Why is this proof incorrect? Statements Reasons 1. Overline OR is congruent to overline OQ, angle N is congruent to angle P 1. Given 2. Overline ON is congruent to overline OP 2. Converse of the Isosceles Triangle Theorem 3. Triangle ONR is congruent to triangle OPQ 3. SAS 4. Angle 3 is congruent to angle 5 4. CPCTCarrow_forwardGiven: AABE ~ ACDE. Prove: AC bisects BD. Note: quadrilateral properties are not permitted in this proof. Step Statement Reason AABE ACDE Given 2 ZDEC ZAEB Vertical angles are congruent try Type of Statement A E B D Carrow_forward
- 2) Based on the given information and the diagram, a. Which congruence statements can be proven? Select all that apply.Given: Overline OR is congruent to overline OQ, angle N is congruent to angle PProve: angle 3 is congruent to angle 5A. Overline ON is congruent to overline OPB. Angle 1 is congruent to angle 2C. Overline ON is congruent to overline OR and overline OP is congruent to overine OQD. angle 1 is congruent to angle 3 and angle 2 is congruent to angle 5There are more than one correct answerarrow_forwardnt/Ray Skew Lines/ J K # H L 艹 G C D E F Diagrams m Three Points th a Protractor Answer Attempt 3 out of 3 el 1 is congruent to Submit Answer 103 Log Out REE Young the → C # $arrow_forward4:54 PM Thu Jan 16 cdn.assess.prod.mheducation.com Question 3 The angle bisectors of APQR are PZ, QZ, and RZ. They meet at a single point Z. (In other words, Z is the incenter of APQR.) Suppose YZ = 22, QZ = 23, mz WPY 38°, and mzXQZ = 54°. Find the following measures. Note that the figure is not drawn to scale. P W Z X R Y mzXQW WZ = = 0 mz XRZ = 0°arrow_forward
- Ja дх dx dx Q3: Define the linear functional J: H()-R by تاریخ (v) = ½a(v, v) - (v) == Let u be the unique weak solution to a(u,v) = L(v) in H₁(2) and suppose that a(...) is a symmetric bilinear form on H() prove that a Buy v) = 1- u is minimizer. 2- u is unique. 3- The minimizer J(u,) can be rewritten under J(u)=u' Au-ub, algebraic form Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer only 1-show that thelation to -Auf in N, u = 0 on a satisfies the stability Vulf and show that V(u-u,)||² = ||vu||2 - ||vu||2 lu-ulls Chu||2 2- Prove that Where =1 ||ul|= a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinear form a(u, v) = (Au, Av) + (Vu, Vv) + (Vu, v) + (u, v) Show that a(u, v) continues and V- elliptic on H(2) (3) (0.0), (3.0)arrow_forwardQ1: A) fill the following: 1- The number of triangular in a triangular region with 5 nodes is quadrilateral with n=5 and m=6 nodés is 2- The complex shape function in 1-D 3- dim(P4(K))=- (7M --- and in the and multiplex shape function in 2-D is 4- The trial space and test space for problem -Auf, u = go on and B) Define the energy norm and prove that the solution u, defined by Galerkin orthogonal satisfies the best approximation. Q2: A) Find the varitional form for the problem 1330 (b(x)) - x²=0, 0arrow_forwardcould you help?arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
An Introduction to Area | Teaching Maths | EasyTeaching; Author: EasyTeaching;https://www.youtube.com/watch?v=_uKKl8R1xBM;License: Standard YouTube License, CC-BY
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=JnLDmw3bbuw;License: Standard YouTube License, CC-BY