Chapter 12, Problem 12.50P

(a) Using the small-signal equivalent circuit in Figure 12.25 for the circuit in Figure $12.24(\text{a}),$ derive the expression for the small-signal current gain $A_{if}=I_o/I_s.$ (b) Using the circuit parameters given in Figure $12.24(\text{a})$ and assuming transistor parameters $h_{FE}=100$ and $V_A=\infty$ calculate the value of $A_{if}$ . Compare this answer with the results of Example 12.9.

To determine

To derive: The expression for the small signal current gain of the circuit.

Answer to Problem 12.50P

The value of the small signal current gain is $\frac{\left\{\frac{R_F\left(\frac{1}{R_B\left|\right|R_{B2}}\right)}{g_{m1}+\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)\left(\frac{1}{R_B\left|\right|R_{B2}}\right)}\left[\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)B-\frac{1}{R_F}\right]-R_{F\text{}}B\right\}}{\frac{-1}{g_{m2}}\left[\left(\frac{R_{C2}+R_L}{R_{C2}}\right)\right]\left\{\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)\left\{\left(\frac{1}{R_2}+g_{m2}\right)+\frac{D}{A\left(\frac{1}{R_B\left|\right|R_{B2}}\right)+g_{m1}}\right\}\left[\left(AB\right)-\frac{1}{R_F}\right]\right\}}$ .

Explanation of Solution

Given:

The given circuit is shown in Figure 1.

  

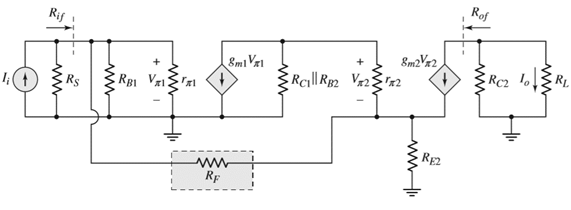
Figure 1

Calculation:

Mark the nodes and redraw the circuit.

The given diagram is shown in Figure 2

  

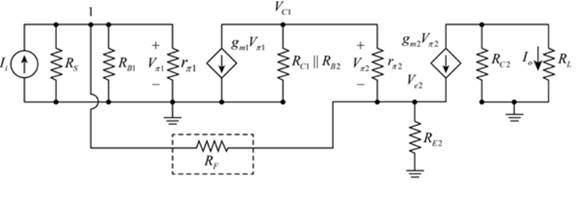
Figure 2

By KCL the expression for the current $I_i$ is given by,

  $\begin{array}{l}{I}_i=\frac{V_{\pi 1}}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}}+\frac{V_{\pi 1}-V_{e2}}{R_F}\\ V_{e2}=V_{\pi 1}\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)-I_i{R}_F\end{array}$

The expression for the node voltage is given by,

  $V_{C1}=V_{\pi 2}+V_{e2}$

Apply KCL at node $V_{C1}$ .

  $\begin{array}{l}{g}_{m1}{V}_{\pi 1}+\frac{V_{C1}}{R_{C1}\left|\right|R_{B2}}+\frac{V_{\pi 2}}{r_{\pi 2}}=0\\ g_{m1}{V}_{\pi 1}+\frac{V_{\pi 2}+V_{e2}}{R_{C1}\left|\right|R_{B2}}+\frac{V_{\pi 2}}{r_{\pi 2}}=0\\ g_{m1}{V}_{\pi 1}+V_{\pi 2}\left(\frac{1}{R_{C1}\left|\right|R_{B2}\left|\right|r_{\pi 2}}\right)+\frac{V_{e2}}{R_{C12}\left|\right|R_{B2}}=0\end{array}$

Substitute $V_{\pi 1}\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)-I_i{R}_F$ for $V_{e2}$ in the above equation.

  $\begin{array}{l}{g}_{m1}{V}_{\pi 1}+V_{\pi 2}\left(\frac{1}{R_{C1}\left|\right|R_{B2}\left|\right|r_{\pi 2}}\right)+\frac{1}{R_{C12}\left|\right|R_{B2}}\left[V_{\pi 1}\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)-I_i{R}_F\right]=0\\ V_{\pi 1}=\frac{I_i{R}_F\left(\frac{1}{R_{C12}\left|\right|R_{B2}}\right)-V_{\pi 2}\left(\frac{1}{R_C\left|\right|R_{B2}\left|\right|r_{\pi 2}}\right)}{g_{m1}+\left[\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)\left(\frac{1}{R_{C12}\left|\right|R_{B2}}\right)\right]}\end{array}$

The expression for the output current is given by,

  $\begin{array}{l}{I}_O=-\left(g_{m2}{V}_{\pi 2}\right)\left(\frac{R_{C2}}{R_{C2}+R_L}\right)\\ V_{\pi 2}=\frac{-I_O}{g_{m2}}\left(\frac{R_{C2}+R_L}{R_{C2}}\right)\end{array}$

Apply KCL at node $V_{e2}$ .

  $\begin{array}{l}\frac{V_{\pi 2}}{r_{\pi 2}}+g_{m2}{V}_{\pi 2}=\frac{V_{e2}}{R_{E2}}+\frac{V_{e2}-V_{\pi 1}}{R_F}\\ \left(\frac{1}{r_{\pi 2}}+g_{m2}\right)V_{\pi 2}+\frac{V_{\pi 1}}{R_F}=\left(\frac{1}{R_{E2}}+\frac{1}{R_F}\right)V_{e2}\end{array}$

Substitute $V_{\pi 1}\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)-I_i{R}_F$ for $V_{e2}$ in the above equation.

  $\begin{array}{l}\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)V_{\pi 2}+\frac{V_{\pi 1}}{R_F}=\left(\frac{1}{R_{E2}}+\frac{1}{R_F}\right)\left(V_{\pi 1}\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)-I_i{R}_F\right)\\ \left(\frac{1}{r_{\pi 2}}+g_{m2}\right)V_{\pi 2}+I_i{R}_F\left(\frac{1}{R_{E2}}+\frac{1}{R_F}\right)=V_{\pi 1}\left\{\left[\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)\left(\frac{1}{R_{E2}}+\frac{1}{R_F}\right)\right]-\frac{1}{R_F}\right\}\end{array}$

Substitute $\frac{I_i{R}_F\left(\frac{1}{R_{C12}\left|\right|R_{B2}}\right)-V_{\pi 2}\left(\frac{1}{R_C\left|\right|R_{B2}\left|\right|r_{\pi 2}}\right)}{g_{m1}+\left[\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)\left(\frac{1}{R_{C12}\left|\right|R_{B2}}\right)\right]}$ for $V_{\pi 1}$ in the above equation.

  $\left[\begin{array}{l}\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)V_{\pi 2}\\ +I_i{R}_F\left(\frac{1}{R_{E2}}+\frac{1}{R_F}\right)\end{array}\right]=\frac{\left[\begin{array}{l}{I}_i{R}_F\left(\frac{1}{R_{C1}\left|\right|R_{B2}}\right)\\ -V_{\pi 2}\left(\frac{1}{R_C\left|\right|R_{B2}\left|\right|r_{\pi 2}}\right)\end{array}\right]}{\left[g_{m1}+\left[\begin{array}{l}\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)\\ \left(\frac{1}{R_{C12}\left|\right|R_{B2}}\right)\end{array}\right]\right]}\left\{\left[\begin{array}{l}\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)\\ \left(\frac{1}{R_{E2}}+\frac{1}{R_F}\right)\end{array}\right]-\frac{1}{R_F}\right\}$

Consider $A=\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}$ , $B=\frac{1}{R_{E2}}+\frac{1}{R_F}$ , $C=\frac{1}{R_{C1}\left|\right|R_{B2}}$ and $D=\frac{1}{R_{C1}\left|\right|R_{B2}\left|\right|r_{\pi 2}}$ in the above equation. So the equation is,

  $\left[\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)V_{\pi 2}+I_i{R}_{F}B\right]=\frac{\left[I_i{R}_{F}C-V_{\pi 2}D\right]}{\left[g_{m1}+AC\right]}\left\{AB-\frac{1}{R_F}\right\}$

  $V_{\pi 2}\left\{\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)+\frac{D}{g_{m1}+AC}\left[AB-\frac{1}{R_F}\right]\right\}=I_i\left\{\frac{R_{F}C}{g_{m1}+AC}\left[AB-\frac{1}{R_F}\right]-R_{F}B\right\}$

  $\left[\frac{-I_O}{g_{m2}}\left(\frac{R_{C2}+R_L}{R_{C2}}\right)\right]\left\{\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)+\frac{D}{g_{m1}+AC}\left[AB-\frac{1}{R_F}\right]\right\}=I_i\left\{\frac{R_{F}C}{g_{m1}+AC}\left[AB-\frac{1}{R_F}\right]-R_{FB}B\right\}$

  $\frac{I_O}{I_i}=\frac{\left\{\frac{R_{F}C}{g_{m1}+AC}\left[AB-\frac{1}{R_F}\right]-R_{F\text{}}B\right\}}{\frac{-1}{g_{m2}}\left[\left(\frac{R_{C2}+R_L}{R_{C2}}\right)\right]\left\{\left\{\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)+\frac{D}{AC+g_{m1}}\right\}\left[\left(AB\right)-\frac{1}{R_F}\right]\right\}}$

Thus, the expression for the small signal current gain is,

  $A_i=\frac{\left\{\frac{R_{F}C}{g_{m1}+AC}\left[AB-\frac{1}{R_F}\right]-R_{F\text{}}B\right\}}{\frac{-1}{g_{m2}}\left[\left(\frac{R_{C2}+R_L}{R_{C2}}\right)\right]\left\{\left\{\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)+\frac{D}{AC+g_{m1}}\right\}\left[\left(AB\right)-\frac{1}{R_F}\right]\right\}}$ …….(1)

Conclusion:

Therefore, the value of the small signal current gain is $\frac{\left\{\frac{R_F\left(\frac{1}{R_B\left|\right|R_{B2}}\right)}{g_{m1}+\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)\left(\frac{1}{R_B\left|\right|R_{B2}}\right)}\left[\left(\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\right)B-\frac{1}{R_F}\right]-R_{F\text{}}B\right\}}{\frac{-1}{g_{m2}}\left[\left(\frac{R_{C2}+R_L}{R_{C2}}\right)\right]\left\{\left(\frac{1}{r_{\pi 2}}+g_{m2}\right)\left\{\left(\frac{1}{R_2}+g_{m2}\right)+\frac{D}{A\left(\frac{1}{R_B\left|\right|R_{B2}}\right)+g_{m1}}\right\}\left[\left(AB\right)-\frac{1}{R_F}\right]\right\}}$ .

To determine

The value of the gain $A_{if}$ for the given specifications.

To compare: The obtained value with the given value of gain. and compare it to the value of 9.58.

Answer to Problem 12.50P

The value of the current gain is $9.58$ and it is approximately equal to the given value of gain.

Explanation of Solution

Given:

The given circuit is shown below.

  

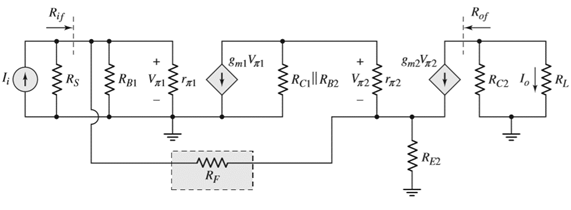
The given value of gain is 9.58.

Also, the values are:

  $\begin{array}{l}{h}_{FE}=100\\ V_A=\infty \end{array}$

Calculation:

The expression to determine the value of the resistance $R_{B1}$ is given by,

  $\begin{array}{c}{R}_{B1}=\frac{\left(80\text{k}\Omega \right)\left(20\text{k}\Omega \right)}{\left(80\text{k}\Omega \right)+\left(20\text{k}\Omega \right)}\\ =16\text{k}\Omega \end{array}$

The expression for the value of the voltage $V_{TH1}$ is given by,

  $\begin{array}{c}{V}_{TH1}=V_{CC}\left(\frac{R_2}{R_2+R_1}\right)\\ =10\text{V}\left(\frac{20\text{k}\Omega }{100\text{k}\Omega }\right)\\ =2\text{V}\end{array}$

The expression to determine the value of the current $I_{B1}$ is given by,

  $I_{BQ1}=\frac{V_{TH1}-V_{BE}\left(\text{on}\right)}{R_{B1}+\left(h_{fe}+1\right)R_{E1}}$

Substitute $2\text{V}$ for $V_{TH1}$ , $0.7\text{V}$ for $V_{BE}$ , $16\text{k}\Omega$ for $R_{B1}$ and $1\text{k}\Omega$ for $R_{E1}$ in the above equation.

  $\begin{array}{c}{I}_{BQ1}=\frac{2\text{V}-0.7\text{V}}{16\text{k}\Omega +\left(100+1\right)1\text{k}\Omega }\\ =0.0111\text{mA}\end{array}$ \

The value of the current $I_{CQ1}$ is calculated as,

  $I_{CQ1}=h_{FE}{I}_{BQ1}$

Substitute $100$ for $h_{FE}$ and $0.0111\text{mA}$ for $I_{BQ1}$ in the above equation.

  $\begin{array}{c}{I}_{CQ1}=\left(100\right)\left(0.0111\text{mA}\right)\\ =1.11\text{mA}\end{array}$

The expression to determine the value of the resistance $R_{B2}$ is given by,

  $\begin{array}{c}{R}_{B2}=R_3\left|\right|R_4\\ =\frac{\left(85\text{k}\Omega \right)\left(15\text{k}\Omega \right)}{\left(85\text{k}\Omega \right)+\left(15\text{k}\Omega \right)}\\ =12.75\text{k}\Omega \end{array}$

The value of the Thevenin voltage is given by,

  $\begin{array}{c}{V}_{TH2}=V_{CC}\left(\frac{R_4}{R_3+R_4}\right)\\ =\left(10\text{V}\right)\left(\frac{15\text{k}\Omega }{15\text{k}\Omega +85\text{k}\Omega }\right)\\ =1.5\text{V}\end{array}$

The expression to determine the value of the current $I_{B2}$ is given by,

  $I_{BQ2}=\frac{V_{TH2}-V_{BE}\left(\text{on}\right)}{R_{B2}+\left(h_{fe}+1\right)R_{E2}}$

Substitute $1.5\text{V}$ for $V_{TH2}$ , $0.7\text{V}$ for $V_{BE}$ , $12.75\text{k}\Omega$ for $R_{B2}$ and $0.5\text{k}\Omega$ for $R_{E2}$ in the above equation.

  $\begin{array}{c}{I}_{BQ2}=\frac{1.5\text{V}-0.7\text{V}}{12.75\text{k}\Omega +\left(100+1\right)0.5\text{k}\Omega }\\ =0.01265\text{mA}\end{array}$ \

The value of the current $I_{CQ2}$ is calculated as,

  $I_{CQ2}=h_{FE}{I}_{BQ2}$

Substitute $100$ for $h_{FE}$ and $0.01265\text{mA}$ for $I_{BQ2}$ in the above equation.

  $\begin{array}{c}{I}_{CQ2}=\left(100\right)\left(0.01265\text{mA}\right)\\ =1.265\text{mA}\end{array}$

The expression to determine the transconductance of first transistor is calculated as,

  $\begin{array}{c}{g}_{m1}=\frac{1.11\text{mA}}{0.026\text{V}}\\ =42.69\text{mA}/\text{V}\end{array}$

The expression to determine the transconductance of second transistor is calculated as,

  $\begin{array}{c}{g}_{m1}=\frac{1.265\text{mA}}{0.026\text{V}}\\ =48.65\text{mA}/\text{V}\end{array}$

The value of the small signal input resistance is calculated as,

  $\begin{array}{c}{r}_{\pi 1}=\frac{h_{FE}}{g_{m1}}\\ =\frac{100}{42.69\text{mA}/\text{V}}\\ =2.34\text{k}\Omega \end{array}$

The value of the small signal input resistance is calculated as,

  $\begin{array}{c}{r}_{\pi 2}=\frac{h_{FE}}{g_{m2}}\\ =\frac{100}{48.65\text{mA}/\text{V}}\\ =2.06\text{k}\Omega \end{array}$

The value of A is calculated as,

  $\begin{array}{c}A=\frac{R_F}{R_s\left|\right|R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\\ \cong \frac{R_F}{R_{B1}\left|\right|r_{\pi 1}\left|\right|R_F}\\ =\frac{10\text{k}\Omega }{16\text{k}\Omega \left|\right|2.34\text{k}\Omega \left|\right|10\text{k}\Omega }\\ =5.896\end{array}$

The value of B is calculated as,

  $\begin{array}{c}B=\frac{1}{R_{E2}}+\frac{1}{R_F}\\ =\frac{1}{0.5\text{k}\Omega }+\frac{1}{10\text{k}\Omega }\\ =2.1\text{m}\end{array}$

The value of C is calculated as,

  $C=\frac{1}{R_B\left|\right|R_{B2}}$

The value of D is calculated as,

  $D=\frac{1}{R_{C1}\left|\right|R_{B2}\left|\right|r_{\pi 2}}$

Substitute $1.7289\text{k}\Omega$ for $R_{C1}\left|\right|R_{B2}$ and $2.06\text{k}\Omega$ for $r_{\pi }$ in the above equation.

  $\begin{array}{c}D=\frac{1}{1.7289\text{k}\Omega \left|\right|2.06\text{k}\Omega }\\ =1.0627\text{m}\end{array}$ , $4\text{k}\Omega$

Substitute $10\text{k}\Omega$ for $R_F$ , $42.69\text{mA}/\text{V}$ for $g_{m1}$ , $48.65\text{mA}/\text{V}$ for $g_{m2}$ , $4\text{k}\Omega$ for $R_{C2}$ , $4\text{k}\Omega$ for $R_E$ , $2.06\text{k}\Omega$ for $r_{\pi 2}$ , $5.896$ for $A$ , $2.1\text{m}$ for $B$ , $0.5784\text{m}$ for $C$ and $1.0672\text{m}$ for $D$ in equation (1).

  $\begin{array}{c}{A}_i=\frac{\left\{\frac{\left(10\text{k}\Omega \right)\left(0.5784\text{m}\right)}{\left(42.69\frac{\text{mA}}{\text{V}}\right)+\left[\begin{array}{l}\left(5.896\right)\\ \left(0.5784\text{m}\right)\end{array}\right]}\left[\left(5.896\right)\left(2.1\text{m}\right)-\frac{1}{\left(10\text{k}\Omega \right)}\right]-\left[\begin{array}{l}\left(10\text{k}\Omega \right)\\ \left(2.1\text{m}\right)\end{array}\right]\right\}}{\frac{-1}{48.65\frac{\text{mA}}{\text{V}}}\left[\left(\frac{\left(4\text{k}\Omega \right)+\left(4\text{k}\Omega \right)}{\left(4\text{k}\Omega \right)}\right)\right]\left\{\begin{array}{l}\left\{\begin{array}{l}\left(\frac{1}{2.06\text{k}\Omega }+48.65\frac{\text{mA}}{\text{V}}\right)\\ +\frac{\left(1.0627\text{m}\right)}{\left(5.896\right)\left(0.5784\text{m}\right)+42.69\frac{\text{mA}}{\text{V}}}\end{array}\right\}\\ \left[\left(\begin{array}{l}\left(5.896\right)\\ \left(2.1\text{m}\right)\end{array}\right)-\frac{1}{\left(10\text{k}\Omega \right)}\right]\end{array}\right\}}\\ =\frac{-19.46}{\left(-0.0411\right)\left(49.4174\right)}\\ =9.58122\end{array}$

The value of the current gain is $9.58122$ and it is approximately equal to the given value of gain.