
For the transistors in the circuit in Figure P 12.53, the parameters are:
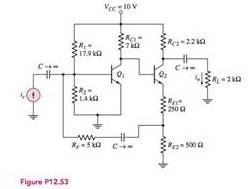
The value of the closed loop current gain of the circuit.
Answer to Problem 12.53P
The value of the current gain is
Explanation of Solution
Given:
The given diagram is shown in Figure 1
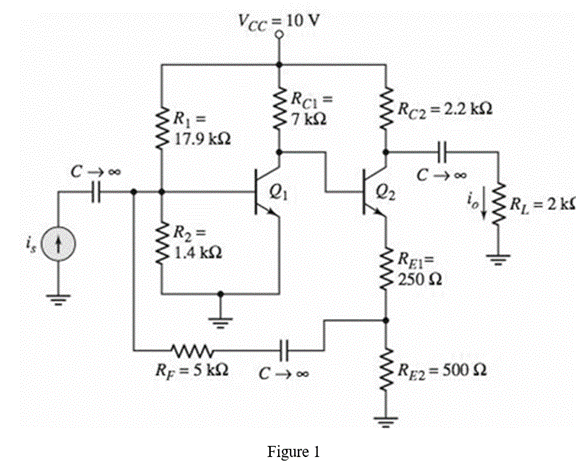
Calculation:
The small signal model of the above circuit is shown below.
The required diagram is shown in Figure 2
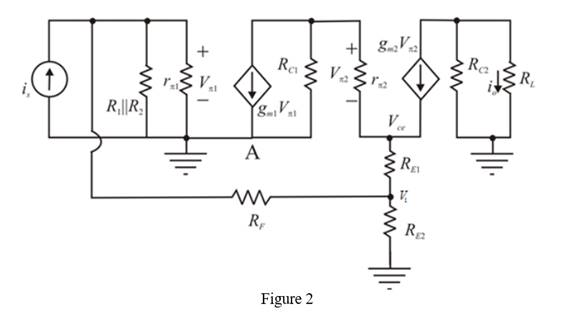
The expression to determine the value of the Thevenin resistance of the circuit is given by,
The Thevenin voltage of the circuit is calculated as,
The expression for the base current of the first transistor is given by,
Substitute
The expression to determine the collector current of the first transistor is given by,
Substitute
The expression to determine the value of the base voltage of the second transistor is given by,
Substitute
The expression for the current
Substitute
The expression to determine the value of the collector current
Substitute
The expression for the transconductance of the first transistor is given by,
Substitute
The expression for the small signal resistance is given by,
Substitute
The expression for the transconductance of the second transistor is given by,
Substitute
The expression for the small signal resistance is given by,
Substitute
Apply KCL at source
Substitute
Apply KCL at node A.
Substitute
Apply KCL at node
Substitute
Apply KCL at
Substitute
Substitute
Substitute
Substitute
Substitute
The expression to determine the value of the output current is given by,
Substitute and
Substitute
Conclusion:
Therefore, the value of the current gain is
Want to see more full solutions like this?
Chapter 12 Solutions
MICROELECT. CIRCUIT ANALYSIS&DESIGN (LL)
- QUESTION [3] A no-load and short-circuit test should be conducted on a 220V/110V, 280VA transformer. a. Draw the circuit diagram for the no-load test and include all measurements that should be made. Also write down the maximum voltage that you should apply to the primary winding and estimate the current drawn from the supply. (5) b. Draw a circuit diagram for the short-circuit test and include all measurements that should be made. Also write down the maximum current that should be allowed to flow in the primary winding and estimated the primary voltage that will cause this value of the current to flow. (5)arrow_forwardOnly expert should solve it pleasearrow_forwardNeed handwritten solution pleasearrow_forward
- Design a lowpass FIR filter using frequency sampling technique having cut-off frequency of T/2 rad/sample. The filter should have linear phase and length of 17.arrow_forwardA dc compound motor having a rating of 10 kW, 1150 r/min, 230 V, 50 A, has the following losses at full-load: bearing friction loss 40 W brush friction loss == 50 W windage loss = 200 W (1) total mechanical losses = 290 W (2) iron losses = 420 W (3) copper loss in the shunt field = 120 W copper losses at full-load: (4) a. in the armature b. in the series field c. in the commutating winding total copper loss in the 500 W 25 W 70 W armature circuit at full-load = 595 Warrow_forward4 What determines the power rating of a ma- chine? -5 If we cover up the vents in a motor, its out- put power must be reduced. Explain. -6 If a motor operates in a cold environment, may we load it above its rated power? Why?arrow_forward
- An electric motor driving a skip hoist with- draws 1.5 metric tons of minerals from a trench 20 m deep every 30 seconds. If the hoist has an overall efficiency of 94 percent, calculate the power output of the motor in horsepower and in kilowatts.arrow_forwardThe efficiency of a motor is always low when it operates at 10 percent of its nominal power rating. Explain.arrow_forwardA dc motor connected to a 240 V line pro- duces a mechanical output of 160 hp. Knowing that the losses are 12 kW, calculate the input power and the line current.arrow_forward
- A 115 V dc generator delivers 120 A to a load. If the generator has an efficiency of 81 percent, calculate the mechanical power needed to drive it [hp].arrow_forwardA machine having class B insulation attains a temperature of 208°C (by resistance) in a torrid ambient temperature of 180°C. a. What is the temperature rise? b. Is the machine running too hot and, if so, by how much?arrow_forward1 Name the losses in a dc motor. 2 What causes iron losses and how can they be reduced? -3 Explain why the temperature of a machine increases as the load increases.arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





