Chapter 1.1, Problem 9SP

Many plane curves in mathematics are named after the people who first investigated them, like the folium of Descartes or the spiral of Archimedes. However. perhaps the strangest name for a curve is the witch of Agnesi. Why a witch?

Maria Gaetana Agnesi (1718—1799) was one of the few recognized women mathematicians of eighteenth-century Italy. She wrote a popular book on analytic geometry, published in 1748, which included an interesting curve that had been studied by Fermat in 1630. The mathematician Guido Grandi showed in 1703 how to construct this curve, which he later called the "versoria," a Latin term for a rope used in sailing. Agnesi used the Italian term for this rope, "versiera,” but in Latin, this same word means a "female goblin.” When Agnesi’s book was translated into English in 1801, the translator used the term “witch” for the curve, instead of rope. The name “witch of Agnesi” has stuck ever since.

The witch of Agnesi is a curve defined as follows: Start with a circle of radius a so that the points $\left(0,0\right)$ and $\left(0,\text{ 2a}\right)$ are points on the circle (Figure 1.12). Let O denote the origin. Choose any other point A on the (tilde, and draw the secant line OA. Let B denote the point at which the line OA intersects the horizontal line through $\left(0,\text{ 2a}\right)$ . The vertical line through B intersects the horizontal line through A at the point P. As the point A varies, the path that the point P travels is the witch of Agnesi curve for the given circle.

Witch of Agnesi curves have applications in physics, including modeling water waves and distributions of spectral lines. In probability theory, the curve describes the probability density function of the Cauchy distribution, In this project you will parameterize these curves.

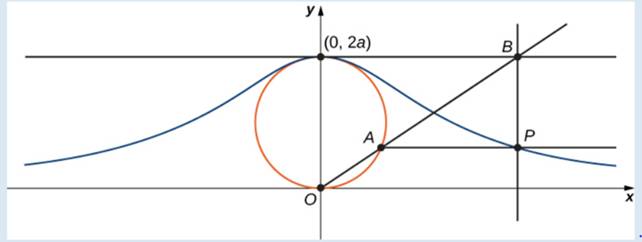
Figure 1.12 As the point A moves around the circle, the point P traces out the witch of

Agnesi curve for the given circle.

9. Use yum parameterization to show that the given witch curve is the graph of the function $f\left(x\right)=\frac{8a^3}{x^2+4a^2}$ .