
Earlier in this section, we looked at the parametric equations for a cycloid, which is the path a point on the edge of a wheel traces as the wheel rolls along a straight path. In this project we look at two different variations of the cycloid. called the curtate and prolate cycloids.
First. let’s revisit the derivation of the parametric equations for a cycloid. Recall that we considered a tenacious ant trying to get home by hanging onto the edge of a bicycle tire. We have assumed the ant climbed onto the tire at the very edge, where the tire touches the ground. As the wheel rolls, the ant moves with the edge of the tire (Figure 1.13).
As we have discussed, we have a lot of flexibility when parameterizing a curve. In this case we let our parameter c represent the angle the tire has rotated through. Looking at Figure 1.13, we see that after the tire has rotated through an angle of t, the Position of the center of the wheel,
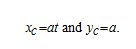
Furthermore, letting
Then
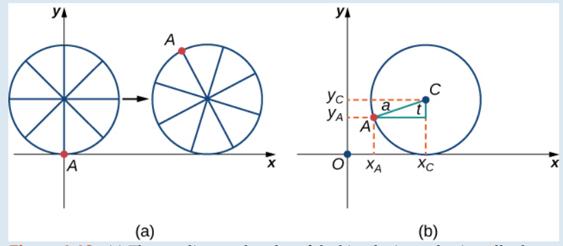
Figure 1.13 (a) The ant clings to die edge of the bicycle tile as the tire rolls along the ground. (b) Using geometry to determine the position of the ant after the tire has rotated through an angle of t.
Note that these are the same parametric representations we had before, but we have now assigned a physical meaning to the parametric variable t.
After a while the am is getting dizzy from going round and round on the edge of the tire. So he climbs up one of the spokes toward the center of the wheel. By climbing toward the center of the wheel. the ant has changed his path of motion. The new path has less up-and-down motion and is called a mutate cycloid (Figure 1.14). As shown in the figure. we let b denote the distance along the spoke flow the center of the wheel to the ant. As before, we let t represent the angle the fire has rotated through. Additionally, we let
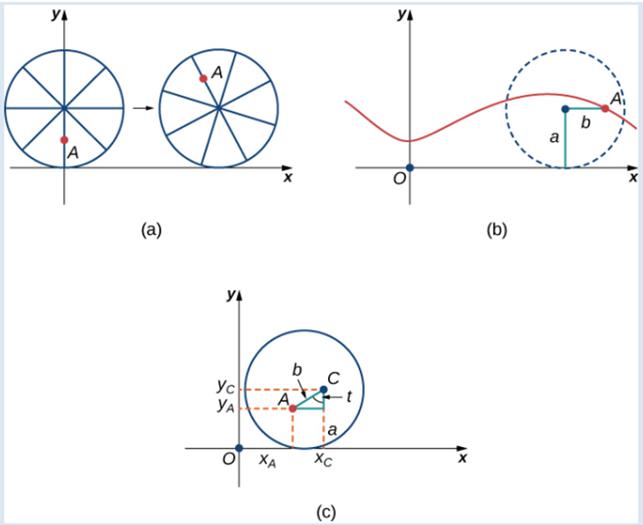
Figure 1.14 (a) The ant climbs up one of the spokes toward the center of the wheel. (b) The ant's path of motion after he climbs closer to the center of the wheel. This is called a mutate cycloid. (c) The new Setup, now that the ant has moved closer to the center of the wheel.
2. Use geometry to find expressions for
Want to see the full answer?
Check out a sample textbook solution
Chapter 1 Solutions
Calculus Volume 3
Additional Math Textbook Solutions
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Elementary Statistics (13th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- Given your fitted regression line, what would be the residual for snake #5 (10 C)?arrow_forwardCalculate the 95% confidence interval around your estimate of r using Fisher’s z-transformation. In your final answer, make sure to back-transform to the original units.arrow_forwardCalculate Pearson’s correlation coefficient (r) between temperature and heart rate.arrow_forward
- Calculate the least squares regression line and write the equation.arrow_forwardTest the null hypothesis that the slope is zero (e.g., β=0).arrow_forwardDo College Students With Part-Time Jobs Sleep Less? College students were surveyed about the number of hours they sleep each night.Group A = With part-time jobs | Group B = Without jobs Group A: 6, 5, 7, 6, 5Group B: 8, 7, 9, 8, 7 Instructions: State your hypothesis and perform a two-sample t-test with all formulas. Create histograms for each group. Label axes and add titles. Comment on the distribution shape (e.g., normal, skewed, etc.).Solve on pen and paperarrow_forward
- H0: mean egg weight is the same in all three diets HA: there is at least one difference among the meansarrow_forwardThis is advanced mathematics question that need detailed solutionsarrow_forwardQuestion: Let F be a field. Prove that F contains a unique smallest subfield, called the prime subfield, which is isomorphic to either Q or Zp for some prime p. Instructions: • Begin by identifying the identity element 1 € F. • Use the closure under addition and inverses to build a subring. • • • Show that either the map ZF or Q →F is an embedding. Prove minimality and uniqueness. Discuss the characteristic of a field and link it to the structure of the prime subfield.arrow_forward
- Topic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning  Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL



