Chapter 11, Problem 50PQ

In a laboratory experiment, an electron with a kinetic energy of 50.5 keV is shot toward another electron initially at rest (Fig. P11.50). (1 eV = 1.602 × 10⁻¹⁹ J) The collision is elastic. The initially moving electron is deflected by the collision.

1. a. Is it possible for the initially stationary electron to remain at rest after the collision? Explain.
2. b. The initially moving electron is detected at an angle of 40.0° from its original path. What is the speed of each electron after the collision?

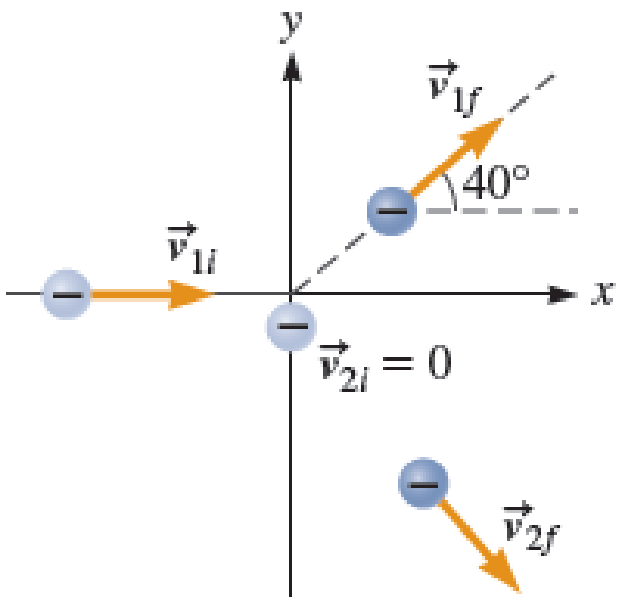
FIGURE P11.50

To determine

Whether it is possible for the initially stationary electron to remain at rest after the collision.

Answer to Problem 50PQ

It is not possible for the initially stationary electron to remain at rest after the collision.

Explanation of Solution

The elastic collision is characterized by the conservation of momentum as well as kinetic energy. For an elastic collision initial momentum of the system before collision should be equal to the momentum of the system after collision.

In the given situation, the initial momentum of the system in $y$ direction is zero since the initially moving electron moves along the $x$ axis and the other electron is at rest. This implies the momentum of the system in $y$ direction after the collision also should be zero. But there is component of momentum in positive $y$ direction for the initially moving electron after collision. This implies the net momentum of the two-electron system after collision in the $y$ direction can be zero only if the electron which was initially at rest has an equal momentum in negative $y$ direction after the collision. For this electron to have momentum, it must move after the collision.

Conclusion:

Thus, it is not possible for the initially stationary electron to remain at rest after the collision.

To determine

The speed of each electron after the collision.

Answer to Problem 50PQ

The speed of initially moving electron after the collision is $1.02\times {10}^8\text{ m/s}$ and that of the other electron is $8.55\times {10}^7\text{ m/s}$ .

Explanation of Solution

The given situation is a two-dimensional elastic collision between two particles of equal mass with initial velocity for one of the particle equal to zero. For such a collision, the angle between the final velocities of the particles after the collision will be equal to $90°$ .

  ${\theta }_1+{\theta }_2=90°$

Here, ${\theta }_1$ is the angle electron 1 makes with the $x$ axis and ${\theta }_2$ is the angle electron 2 makes with the $x$ axis.

Rearrange the above equation for ${\theta }_2$ .

  ${\theta }_2=90°-{\theta }_1$

It is given that the value of ${\theta }_1$ is $40°$ .

Substitute $40°$ for ${\theta }_1$ in the above equation to find the value of ${\theta }_2$ .

  $\begin{array}{c}{\theta }_2=90°-40°\\ =50°\end{array}$

Write the expression for the conservation of momentum in $x$ direction.

  $m_e{v}_{1i}=m_e{v}_{1f_x}+m_e{v}_{2f_x}$                                                                                               (I)

Here, $m_e$ is the mass of the electron, $v_{1i}$ is the initial speed of the electron which is in the $x$ direction, $v_{1f_x}$ is the component of final velocity of the electron 1 in $x$ direction and $v_{2f_x}$ is the component of final velocity of the electron 2 in $x$ direction.

Write the expression for $v_{1f_x}$ .

  $v_{1f_x}=v_{1f}\cos {\theta }_1$

Here, $v_{1f}$ is the velocity of electron 1 after collision.

Substitute $40°$ for ${\theta }_1$ in the above equation to find the expression for of $v_{1f_x}$ .

  $v_{1f_x}=v_{1f}\cos 40°$                                                                                                      (II)

Write the expression for $v_{2f_x}$ .

  $v_{2f_x}=v_{2f}\cos {\theta }_2$

Here, $v_{2f}$ is the velocity of electron 2 after collision.

Substitute $50°$ for ${\theta }_2$ in the above equation to find the expression for of $v_{2f_x}$ .

  $v_{2f_x}=v_{2f}\cos 50°$                                                                                                    (III)

Put equations (II) and (III) in equation (I).

  $m_e{v}_{1i}=m_e{v}_{1f}\cos 40°+m_e{v}_{2f}\cos 50°$                                                                     (IV)

The momentum in $y$ direction for the two-electron system before collision is zero.

Write the expression for the conservation of momentum in $y$ direction.

  $0=m_e{v}_{1f_y}+m_e{v}_{2f_y}$                                                                                                (V)

Here, $v_{1f_y}$ is the component of final velocity of the electron 1 in $y$ direction and $v_{2f_y}$ is the component of final velocity of the electron 2 in $y$ direction.

Write the expression for $v_{1f_y}$ .

  $v_{1f_y}=v_{1f}\sin {\theta }_1$

Substitute $40°$ for ${\theta }_1$ in the above equation to find the expression for of $v_{1f_y}$ .

  $v_{1f_y}=v_{1f}\sin 40°$                                                                                                     (VI)

Write the expression for $v_{2f_y}$ .

  $v_{2f_y}=-v_{2f}\sin {\theta }_2$

The negative sign is due to the fact that the electron 2 moves in negative $y$ direction.

Substitute $50°$ for ${\theta }_2$ in the above equation to find the expression for of $v_{2f_y}$ .

  $v_{2f_y}=-v_{2f}\sin 50°$                                                                                                  (VII)

Put equations (VI) and (VII) in equation (V) and rearrange it for $v_{1f}$ .

  $\begin{array}{c}{m}_e{v}_{1f}\sin 40°=m_e{v}_{2f}\sin 50°\\ v_{1f}=\frac{v_{2f}\sin 50°}{\sin 40°}\end{array}$                                                                                (VIII)

Put the above equation in equation (IV) and rearrange it for $v_{2f}$ .

  $\begin{array}{c}{m}_e{v}_{1i}=m_e\left(\frac{v_{2f}\sin 50°}{\sin 40°}\right)\cos 40°+m_e{v}_{2f}\cos 50°\\ v_{1i}=v_{2f}\left(\frac{\sin 50°}{\sin 40°}\cos 40°+\cos 50°\right)\\ =1.56v_{2f}\\ v_{2f}=0.643v_{1i}\end{array}$                                                  (IX)

Put equation (IX) in equation (VIII).

  $\begin{array}{c}{v}_{1f}=\frac{\left(0.643v_{1i}\right)\sin 50°}{\sin 40°}\\ =0.766v_{1i}\end{array}$                                                                                            (X)

Write the equation for the initial kinetic energy of electron 1.

  $K=\frac{1}{2}{m}_e{v}_{1i}^2$

Here, $K$ is the initial kinetic energy of electron 1.

Rewrite the above equation for $v_{1i}$ .

  $\begin{array}{c}{v}_{1i}^2=\frac{2K}{m_e}\\ v_{1i}=\sqrt{\frac{2K}{m_e}}\end{array}$                                                                                                              (XI)

Conclusion:

It is given that the initial kinetic energy of electron 1 is $50.5\text{ keV}$. The mass of the electron is $9.11\times {10}^{-31}\text{ kg}$ .

Substitute $50.5\text{ keV}$ for $K$ and $9.11\times {10}^{-31}\text{ kg}$ for $m_e$ in equation (XI) to find $v_{1i}$ .

  $\begin{array}{c}{v}_{1i}=\sqrt{\frac{2\left(50.5\text{ keV}\frac{1.602\times {10}^{-16}\text{ J}}{1\text{ keV}}\right)}{9.11\times {10}^{-31}\text{ kg}}}\\ =1.33\times {10}^8\text{ m/s}\end{array}$

Substitute $1.33\times {10}^8\text{ m/s}$ for $v_{1i}$ in equation (X) to find the value of $v_{1f}$ .

  $\begin{array}{c}{v}_{1f}=0.766\left(1.33\times {10}^8\text{ m/s}\right)\\ =1.02\times {10}^8\text{ m/s}\end{array}$

Substitute $1.33\times {10}^8\text{ m/s}$ for $v_{1i}$ in equation (IX) to find the value of $v_{2f}$ .

  $\begin{array}{c}{v}_{2f}=0.643\left(1.33\times {10}^8\text{ m/s}\right)\\ =8.55\times {10}^7\text{ m/s}\end{array}$

Therefore, the speed of initially moving electron after the collision is $1.02\times {10}^8\text{ m/s}$ and that of the other electron is $8.55\times {10}^7\text{ m/s}$ .