Chapter 10.4, Problem 1P

Students sometimes get confused about the relationship between squares and rectangles. Explain this relationship In your own words, using our (short) definitions of these shapes

To determine

To explain: The relationship between squares and rectangles.

Explanation of Solution

Consider a square shown in Figure 1.

 

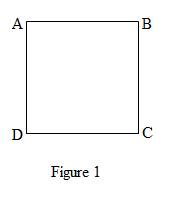
The above Figure 1 represents square ABCD.

The sides of square AB, BC,CD, and DA are equal.

Consider a rectangle shown in Figure 2.

 

The above Figure 2 represents rectangle EFGH.

The sides of square EF, GH are length of the rectangle and are equal in size.

The sides of square EH, FG is breadth of the rectangle and is equal in size.

All angles of rectangle are right angle.

Therefore, it can be observed that the square has all side equals and every angle form right angle similar to rectangle.

Therefore, every rectangle can be square but every square cannot be rectangle.