
Concept explainers
Two 89 × 64-mm angles are bolted together as shown for use as a column of 2.4-m effective length to carry a centric load of 325 kN. Knowing that the angles available have thicknesses of 6.4 mm, 9.5 mm, and 12.7 mm, use allowable stress design to determine the lightest angles that can be used. Use σY = 250 MPa and E = 200 GPa.
Fig. P10.84
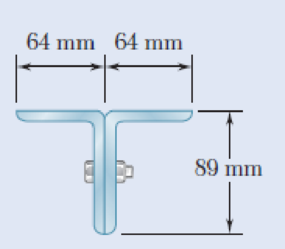
Find the lightest angles that can be used.
Answer to Problem 84P
The lightest angle that can be used for the design is
Explanation of Solution
Given information:
The effective length of the column is
The allowable yield strength of the steel is
The modulus of elasticity of the steel is
The centric load acting in the column is
Calculation:
Consider the thickness of the angle section as 9.5 mm.
Refer to Appendix C “Properties of Rolled-Steel Shapes” in the textbook.
For
The cross sectional area of the angle (A) is
The moment of inertia in x-axis is
The moment of inertia in y-axis is
The centroid distance from the flange in x-axis is
The area of the two angle section is
The moment of inertia in x-axis is
Find the moment of inertia in y-axis using the relation.
Substitute
The minimum moment of inertia is
Find the minimum radius of gyration (r) using the relation.
Substitute
Find the slenderness ratio
Here, the modulus of elasticity of the material is E and the allowable yield strength is
Substitute 200 GPa for E and 250 MPa for
Find the ratio of effective length
Find the effective stress
Substitute 200 GPa for E and 97.22 for
Find the critical stress
Substitute 250 MPa for
Calculate the allowable stress
Substitute 151.472 MPa for
Calculate the allowable load
Substitute 90.702 MPa for
The centric load is greater than the allowable load. Hence, the design is unsafe.
Consider the thickness of the angle section as 12.7 mm.
Refer to Appendix C “Properties of Rolled-Steel Shapes” in the textbook.
For
The cross sectional area of the angle (A) is
The moment of inertia in x-axis is
The moment of inertia in y-axis is
The centroid distance from the flange in x-axis is
The area of the two angle section is
The moment of inertia in x-axis is
Find the moment of inertia in y-axis using the relation.
Substitute
The minimum moment of inertia is
Find the minimum radius of gyration (r) using the relation.
Substitute
Find the slenderness ratio
Here, the modulus of elasticity of the material is E and the allowable yield strength is
Substitute 200 GPa for E and 250 MPa for
Find the ratio of effective length
Find the effective stress
Substitute 200 GPa for E and 95.12 for
Find the critical stress
Substitute 250 MPa for
Calculate the allowable stress
Substitute 154.753 MPa for
Calculate the allowable load
Substitute 92.667 MPa for
The centric load is less than the allowable load. Hence, the design is unsafe.
Therefore, the lightest angle that can be used for the design is
Want to see more full solutions like this?
Chapter 10 Solutions
Mechanics of Materials, 7th Edition
- PROBLEM 3.46 The solid cylindrical rod BC of length L = 600 mm is attached to the rigid lever AB of length a = 380 mm and to the support at C. When a 500 N force P is applied at A, design specifications require that the displacement of A not exceed 25 mm when a 500 N force P is applied at A For the material indicated determine the required diameter of the rod. Aluminium: Tall = 65 MPa, G = 27 GPa. Aarrow_forwardFind the equivalent mass of the rocker arm assembly with respect to the x coordinate. k₁ mi m2 k₁arrow_forward2. Figure below shows a U-tube manometer open at both ends and containing a column of liquid mercury of length l and specific weight y. Considering a small displacement x of the manometer meniscus from its equilibrium position (or datum), determine the equivalent spring constant associated with the restoring force. Datum Area, Aarrow_forward
- 1. The consequences of a head-on collision of two automobiles can be studied by considering the impact of the automobile on a barrier, as shown in figure below. Construct a mathematical model (i.e., draw the diagram) by considering the masses of the automobile body, engine, transmission, and suspension and the elasticity of the bumpers, radiator, sheet metal body, driveline, and engine mounts.arrow_forward3.) 15.40 – Collar B moves up at constant velocity vB = 1.5 m/s. Rod AB has length = 1.2 m. The incline is at angle = 25°. Compute an expression for the angular velocity of rod AB, ė and the velocity of end A of the rod (✓✓) as a function of v₂,1,0,0. Then compute numerical answers for ȧ & y_ with 0 = 50°.arrow_forward2.) 15.12 The assembly shown consists of the straight rod ABC which passes through and is welded to the grectangular plate DEFH. The assembly rotates about the axis AC with a constant angular velocity of 9 rad/s. Knowing that the motion when viewed from C is counterclockwise, determine the velocity and acceleration of corner F.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





