
To find: The area of the common region enclosed by the circles
Answer to Problem 52E
The area of the region enclosed by the given circles is
Explanation of Solution
Given information: Equations of two circles are
Formula used: The double-angle formula for cosine function is given by:
Calculation:
Equate the given equations of circles and determine the value of
According to the fact
Draw the graph of region enclosed by the circles as shown below.
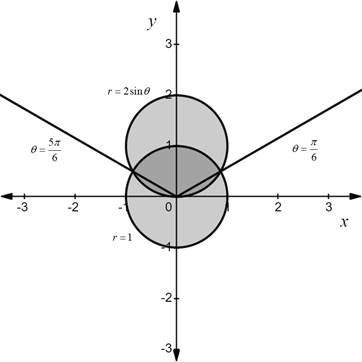
Figure (1)
Here,
From the above graph it can be observed that the common region enclosed by the given circles is same as the region enclosed by the polar curve
Also, the common region enclosed by the given circles is symmetrical with respect to the positive
Calculate the area of the region enclosed by the circles.
Evaluate the obtained integral.
Further simplify.
Apply the identity
Evaluate the integral
For
Using the above results determine the integral
Therefore, the area of the region enclosed by the given circles is
Chapter 10 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- Use the information to find and compare Δy and dy. (Round your answers to four decimal places.) y = x4 + 7 x = −3 Δx = dx = 0.01 Δy = dy =arrow_forward4. A car travels in a straight line for one hour. Its velocity, v, in miles per hour at six minute intervals is shown in the table. For each problem, approximate the distance the car traveled (in miles) using the given method, on the provided interval, and with the given number of rectangles or trapezoids, n. Time (min) 0 6 12 18|24|30|36|42|48|54|60 Speed (mph) 0 10 20 40 60 50 40 30 40 40 65 a.) Left Rectangles, [0, 30] n=5 b.) Right Rectangles, [24, 42] n=3 c.) Midpoint Rectangles, [24, 60] n=3 d.) Trapezoids, [0, 24] n=4arrow_forwardThe bracket BCD is hinged at C and attached to a control cable at B. Let F₁ = 275 N and F2 = 275 N. F1 B a=0.18 m C A 0.4 m -0.4 m- 0.24 m Determine the reaction at C. The reaction at C N Z F2 Darrow_forward
- The correct answer is C,i know that we need to use stokes theorem and parametrize the equations then write the equation F with respect to the curve but i cant seem to find a way to do it, the integral should be from 0 to 2pi but i might be wrongcould you show me the steps to get to 18piarrow_forwardA 10-ft boom is acted upon by the 810-lb force as shown in the figure. D 6 ft 6 ft E B 7 ft C 6 ft 4 ft W Determine the tension in each cable and the reaction at the ball-and-socket joint at A. The tension in cable BD is lb. The tension in cable BE is lb. The reaction at A is ( lb) i + Ib) j. (Include a minus sign if necessary.)arrow_forwardthe correct answer is A could you show me whyarrow_forward
- Good Day, Kindly assist me with this query.arrow_forwardon donne f(x) da fonction derive dhe do fonction fcsos calcule f'(x) orans chacun des Cas sulants: 3 1) f(x)=5x-11, 2- f (x) = ->³ 3-1(x) = x² 12x +π; 4-f(x)=- 5-f(x) = 33-4x6-609)=-3x²+ 7= f(x) = x + 1.8-f(x) = 4 s-f(x) = x++ X+1 -x-1 2 I 3x-4 девоarrow_forwardThe correct answer is Ccould you show me how to do it by finding a0 and and akas well as setting up the piecewise function and integratingarrow_forward
- T 1 7. Fill in the blanks to write the calculus problem that would result in the following integral (do not evaluate the interval). Draw a graph representing the problem. So π/2 2 2πxcosx dx Find the volume of the solid obtained when the region under the curve on the interval is rotated about the axis.arrow_forward38,189 5. Draw a detailed graph to and set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the curve: y = cos²x_for_ |x| ≤ and the curve y y = about the line x = =플 2 80 F3 a FEB 9 2 7 0 MacBook Air 3 2 stv DGarrow_forwardFind f(x) and g(x) such that h(x) = (fog)(x) and g(x) = 3 - 5x. h(x) = (3 –5x)3 – 7(3 −5x)2 + 3(3 −5x) – 1 - - - f(x) = ☐arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





