Chapter 10.3, Problem 3E

a)

To determine

To plot: The point with the given rectangular coordinates and find the two sets of corresponding polar coordinates.

Answer to Problem 3E

The rectangular coordinates are shown in Figure (1) and the two sets of corresponding polar coordinates are $\left(\sqrt{2},\frac{7\pi }{4}\right)$ and $\left(\sqrt{2},\frac{15\pi }{4}\right)$ .

Explanation of Solution

Given information: A rectangular coordinate is given as $\left(-1,1\right)$ .

Formula used:

Let the point P have polar coordinates $\left(r,\theta \right)$ and rectangular coordinates $\left(x,y\right)$. The formula to convert rectangular coordinates to polar coordinates is given as:

  $\begin{array}{l}r=\sqrt{x^2+y^2}\\ \theta ={\tan }^{-1}\left(\frac{y}{x}\right)\end{array}$

The other polar coordinates of P can be calculated as $\left(r,\theta +2n\pi \right)$ or $\left(-r,\theta +\left(2n+1\right)\pi \right)$ where $n$ is any integer.

Calculation:

Plot $\left(-1,1\right)$ on rectangular coordinate system as shown below.

  

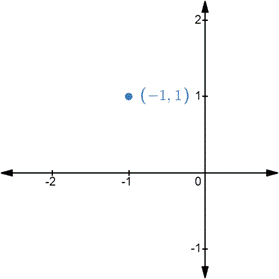
Figure (1)

Find the value of $r$ .

  $\begin{array}{c}r=\sqrt{x^2+y^2}\\ =\sqrt{{\left(-1\right)}^2+1^2}\\ =\sqrt{2}\end{array}$

Find the value of $\theta$ .

  $\begin{array}{c}\theta ={\tan }^{-1}\left(\frac{y}{x}\right)\\ ={\tan }^{-1}\left(\frac{1}{-1}\right)\\ =\frac{-\pi }{4}\end{array}$

Thus, the corresponding polar coordinate is $\left(\sqrt{2},-\frac{\pi }{4}\right)$ .

Substitute $1$ for $n$ in $\left(r,\theta +2n\pi \right)$ to find other set of polar coordinates.

  $\begin{array}{c}\left(r,\theta +2n\pi \right)=\left(\sqrt{2},-\frac{\pi }{4}+2\times 1\times \pi \right)\\ =\left(\sqrt{2},\frac{7\pi }{4}\right)\end{array}$

Substitute $2$ for $n$ in $\left(r,\theta +2n\pi \right)$ to find other set of polar coordinates.

  $\begin{array}{c}\left(r,\theta +2n\pi \right)=\left(\sqrt{2},-\frac{\pi }{4}+2\times 2\times \pi \right)\\ =\left(\sqrt{2},\frac{15\pi }{4}\right)\end{array}$

Thus, the two sets of corresponding polar coordinates are $\left(\sqrt{2},\frac{7\pi }{4}\right)$ and $\left(\sqrt{2},\frac{15\pi }{4}\right)$ .

b)

To determine

To plot: The point with the given rectangular coordinates and find the two sets of corresponding polar coordinates.

Answer to Problem 3E

The rectangular coordinates are shown in Figure (2) and the two sets of corresponding polar coordinates are $\left(2,\frac{5\pi }{3}\right)$ and $\left(2,\frac{11\pi }{3}\right)$ .

Explanation of Solution

Given information: A rectangular coordinate is given as $\left(1,-\sqrt{3}\right)$ .

Formula used:

Let the point P have polar coordinates $\left(r,\theta \right)$ and rectangular coordinates $\left(x,y\right)$. The formula to convert rectangular coordinates to polar coordinates is given as:

  $\begin{array}{l}r=\sqrt{x^2+y^2}\\ \theta ={\tan }^{-1}\left(\frac{y}{x}\right)\end{array}$

The other polar coordinates of P can be calculated as $\left(r,\theta +2n\pi \right)$ or $\left(-r,\theta +\left(2n+1\right)\pi \right)$ where $n$ is any integer.

Calculation:

Plot $\left(1,-\sqrt{3}\right)$ on rectangular coordinate system as shown below.

  

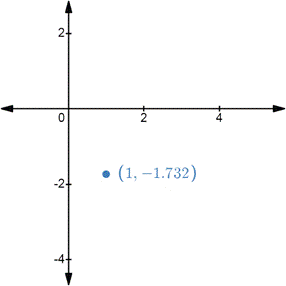
Figure (2)

Find the value of $r$ .

  $\begin{array}{c}r=\sqrt{x^2+y^2}\\ =\sqrt{1^2+{\left(-\sqrt{3}\right)}^2}\\ =\sqrt{1+3}\\ =2\end{array}$

Find the value of $\theta$ .

  $\begin{array}{c}\theta ={\tan }^{-1}\left(\frac{y}{x}\right)\\ ={\tan }^{-1}\left(\frac{-\sqrt{3}}{1}\right)\\ =-\frac{\pi }{3}\end{array}$

Thus, the corresponding polar coordinate is $\left(2,-\frac{\pi }{3}\right)$ .

Substitute $1$ for $n$ in $\left(r,\theta +2n\pi \right)$ to find other set of polar coordinates.

  $\begin{array}{c}\left(r,\theta +2n\pi \right)=\left(2,-\frac{\pi }{3}+2\times 1\times \pi \right)\\ =\left(2,\frac{5\pi }{3}\right)\end{array}$

Substitute $2$ for $n$ in $\left(r,\theta +2n\pi \right)$ to find other set of polar coordinates.

  $\begin{array}{c}\left(r,\theta +2n\pi \right)=\left(2,-\frac{\pi }{3}+2\times 2\times \pi \right)\\ =\left(2,\frac{11\pi }{3}\right)\end{array}$

Therefore, the two sets of corresponding polar coordinates are $\left(2,\frac{5\pi }{3}\right)$ and $\left(2,\frac{11\pi }{3}\right)$ .

c)

To determine

To plot: The point with the given rectangular coordinates and find the two sets of corresponding polar coordinates.

Answer to Problem 3E

The rectangular coordinates are shown in Figure (3) and the two sets of corresponding polar coordinates are $\left(3,\frac{5\pi }{2}\right)$ and $\left(3,\frac{9\pi }{2}\right)$ .

Explanation of Solution

Given information: A rectangular coordinate is given as $\left(0,3\right)$ .

Formula used:

Let the point P have polar coordinates $\left(r,\theta \right)$ and rectangular coordinates $\left(x,y\right)$. The formula to convert rectangular coordinates to polar coordinates is given as:

  $\begin{array}{l}r=\sqrt{x^2+y^2}\\ \theta ={\tan }^{-1}\left(\frac{y}{x}\right)\end{array}$

The other polar coordinates of P can be calculated as $\left(r,\theta +2n\pi \right)$ or $\left(-r,\theta +\left(2n+1\right)\pi \right)$ where $n$ is any integer.

Calculation:

Plot $\left(0,3\right)$ on rectangular coordinate system as shown below.

  

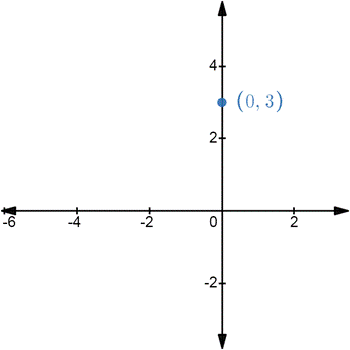
Figure (3)

Find the value of $r$ .

  $\begin{array}{c}r=\sqrt{x^2+y^2}\\ =\sqrt{0^2+3^2}\\ =3\end{array}$

Find the value of $\theta$ .

  $\begin{array}{c}\theta ={\tan }^{-1}\left(\frac{y}{x}\right)\\ ={\tan }^{-1}\left(\frac{3}{0}\right)\\ =\frac{\pi }{2}\end{array}$

Thus, the corresponding polar coordinate is $\left(3,\frac{\pi }{2}\right)$ .

Substitute $1$ for $n$ in $\left(r,\theta +2n\pi \right)$ to find other set of polar coordinates.

  $\begin{array}{c}\left(r,\theta +2n\pi \right)=\left(3,\frac{\pi }{2}+2\times 1\times \pi \right)\\ =\left(3,\frac{5\pi }{2}\right)\end{array}$

Substitute $2$ for $n$ in $\left(r,\theta +2n\pi \right)$ to find other set of polar coordinates.

  $\begin{array}{c}\left(r,\theta +2n\pi \right)=\left(3,\frac{\pi }{2}+2\times 2\times \pi \right)\\ =\left(3,\frac{9\pi }{2}\right)\end{array}$

Therefore, the two sets of corresponding polar coordinates are $\left(3,\frac{5\pi }{2}\right)$ and $\left(3,\frac{9\pi }{2}\right)$ .

d)

To determine

To plot: The point with the given rectangular coordinates and find the two sets of corresponding polar coordinates.

Answer to Problem 3E

The rectangular coordinates are shown in Figure (4) and the two sets of corresponding polar coordinates are $\left(1,3\pi \right)$ and $\left(1,5\pi \right)$ .

Explanation of Solution

Given information: A rectangular coordinate is given as $\left(-1,0\right)$ .

Formula used: Let the point P have polar coordinates $\left(r,\theta \right)$ and rectangular coordinates $\left(x,y\right)$. The formula to convert rectangular coordinates to polar coordinates is given as:

  $\begin{array}{l}r=\sqrt{x^2+y^2}\\ \theta ={\tan }^{-1}\left(\frac{y}{x}\right)\end{array}$

The other polar coordinates of P can be calculated as $\left(r,\theta +2n\pi \right)$ or $\left(-r,\theta +\left(2n+1\right)\pi \right)$ where $n$ is any integer.

Calculation:

Plot $\left(-1,0\right)$ on rectangular coordinate system as shown below.

  

Find the value of $r$ .

  $\begin{array}{c}r=\sqrt{x^2+y^2}\\ =\sqrt{{\left(-1\right)}^2+0}\\ =1\end{array}$

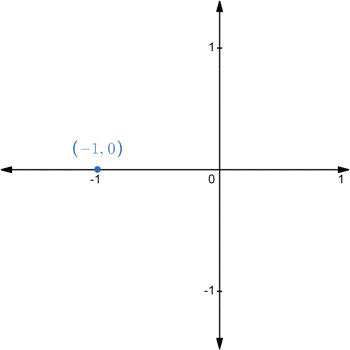
Find the value of $\theta$ .

  $\begin{array}{c}\theta ={\tan }^{-1}\left(\frac{y}{x}\right)\\ ={\tan }^{-1}\left(\frac{0}{-1}\right)\\ =\pi \end{array}$

Thus, the corresponding polar coordinate is $\left(1,\pi \right)$ .

Substitute $1$ for $n$ in $\left(r,\theta +2n\pi \right)$ to find other set of polar coordinates.

  $\begin{array}{c}\left(r,\theta +2n\pi \right)=\left(1,\pi +2\times 1\times \pi \right)\\ =\left(1,3\pi \right)\end{array}$

Substitute $2$ for $n$ in $\left(r,\theta +2n\pi \right)$ to find other set of polar coordinates.

  $\begin{array}{c}\left(r,\theta +2n\pi \right)=\left(1,\pi +2\times 2\times \pi \right)\\ =\left(1,5\pi \right)\end{array}$

Therefore, the two sets of corresponding polar coordinates are $\left(1,3\pi \right)$ and $\left(1,5\pi \right)$ .