Chapter 10.3, Problem 57E

To determine

To calculate: To solve the area of the region inside the polar curve.

Answer to Problem 57E

The area of the region is $\pi$ .

Explanation of Solution

Given information: The given curve as:

The area of the region inside the circle and outside the cardioid. The polar curves are $r=3\cos \left(\theta \right)$ and $r=1+\cos \theta$ .

Calculation:

The sketch of the polar curve is:

  

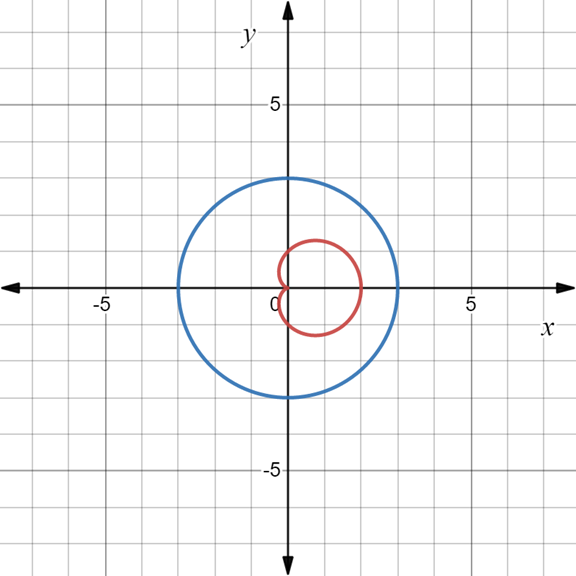
The area of the given curve can be calculated as:

  $A=\frac{1}{2}{\displaystyle {\int }_a^b{r}^{2}d\theta }$ .

The intersection points f this curve are:

  $\begin{array}{c}1+\cos \theta =3\cos \theta \\ 1=2\cos \theta \\ \cos \theta =\frac{1}{2}\\ \theta =\frac{\pi }{3},-\frac{\pi }{3}\end{array}$

Based on the symmetry with respect to the $x-$ axis can be calculated as:

  $\begin{array}{c}A=2\times \frac{1}{2}{\displaystyle {\int }_0^{\frac{\pi }{3}}\left[{\left(3\cos \left(\theta \right)\right)}^2-{\left(1+\cos \theta \right)}^2\right]}d\theta \\ A={\displaystyle {\int }_0^{\frac{\pi }{3}}\left[\left(9{\cos }^2\left(\theta \right)\right)-1-2\cos \theta -{\cos }^2\left(\theta \right)\right]}d\theta \\ A={\displaystyle {\int }_0^{\frac{\pi }{3}}\left[8{\cos }^2\left(\theta \right)-1-2\cos \theta \right]}d\theta \\ A={\displaystyle {\int }_0^{\frac{\pi }{3}}\left[8\frac{\cos \left(2\theta \right)+1}{2}-1-2\cos \theta \right]}d\theta \\ A={\displaystyle {\int }_0^{\frac{\pi }{3}}\left[4\cos \left(2\theta \right)+4-1-2\cos \theta \right]}d\theta \\ A={\left[4\frac{\sin \left(2\theta \right)}{2}+3\theta -2\sin \theta \right]}_0^{\frac{\pi }{3}}\\ A=2\sin \frac{2\pi }{3}-2\sin \frac{\pi }{3}+\frac{3\pi }{3}\\ A=\pi +\sqrt{3}-\sqrt{3}\\ A=\pi \end{array}$

The area of the curve is $\pi$ .