
Concept explainers
To calculate:
The probability that a point chosen at random inside the cube is also inside a sphere.
Answer to Problem 25E
The probability that a point chosen at random inside the cube is also inside a sphere is
Explanation of Solution
Given information:
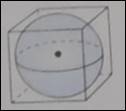
Calculation:
The question is related to probability of the event.
It is given that information about the radius of the provided cube, and sphere inscribed in it and it is used to obtain a probability of randomly selected point being in the cube and sphere.
Thus probabilities that a randomly selected point in the cube, is also in the spheres is obtained as below,
Hence, The probability that a point chosen at random inside the cube is also inside a sphere is
Chapter 10 Solutions
Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015
- Find the values of n, if the points (n + 1, 2n), (3n, 2n + 3) and (5n + 1,5n) are collinear. Find the value of k that the four points (4,1,2), (5, k, 6), (5,1,-1) and (7,4,0) are coplanar. Find the value of r if the area of the triangle is formed by the points (-3,6),(4,4) and (r,-2) is 12 sq units. Find the volume of tetrahedron whose vertices are A(1,1,0), B(-4,3,6), C(-1,0,3) and D(2,4,-5).arrow_forward- Consider the following system of linear equations in the variables a,b,c,d: 5a-3b 7c - 2d = 2 2ab 2c+ 5d = -3 → (*) 4a 3b 5d = 3 6a b+2c+ 7d = −7 (a) Solve the system (*) by using Gauss elimination method. (b) Solve the system (*) by using Cramer's rule method.arrow_forwardSolve for a 25 55 30 a=?arrow_forward
- 9:41 … 93 Applying an Exponential Function to Newton's Law of Cooling 60. Water in a water heater is originally Aa ← 122°F. The water heater is shut off and the water cools to the temperature of the surrounding air, which is 60°F. The water cools slowly because of the insulation inside the heater, and the value of k is measured as 0.00351. a. Write a function that models the temperature T (t) (in °F) of the water t hours after the water heater is shut off. b. What is the temperature of the water 12 hr after the heater is shut off? Round to the nearest degree. c. Dominic does not like to shower with water less than 115°F. If Dominic waits 24 hr. will the water still be warm enough for a shower? Mixed Exercises ger-ui.prod.mheducation.comarrow_forwardPlease use the infinite series formula and specify how you did each step. Thank you.arrow_forward8) Solve the given system using the Gaussian Elimination process. 2x8y = 3 (-6x+24y = −6arrow_forward
- 7) Solve the given system using the Gaussian Elimination process. (5x-4y = 34 (2x - 2y = 14arrow_forward33 (a) (b) Let A(t) = = et 0 0 0 cos(t) sin(t) 0-sin(t) cos(t)) For any fixed tЄR, find det(A(t)). Show that the matrix A(t) is invertible for any tЄ R, and find the inverse (A(t))¹.arrow_forwardUse the infinite geometric sum to convert .258 (the 58 is recurring, so there is a bar over it) to a ratio of two integers. Please go over the full problem, specifying how you found r. Thank you.arrow_forward
- H.w: Find the Eigen vectors for the largest Eigen value of the system X1+ +2x3=0 3x1-2x2+x3=0 4x1+ +3x3=0arrow_forwardneed help with 5 and 6 pleasearrow_forward1) Given matrix A below, answer the following questions: a) What is the order of the matrix? b) What is the element a13? c) What is the element a₁₁? 4 -1arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





