
Concept explainers
a)
To determine: The fraction defective in each sample.
Introduction: Quality is a measure of excellence or a state of being free from deficiencies, defects and important variations. It is obtained by consistent and strict commitment to certain standards to attain uniformity of a product to satisfy consumers’ requirement.
a)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Calculation of fraction defective in each sample:
| n | 200 | |||
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
| Prop defective | 0.02 | 0.01 | 0.025 | 0.045 |
Excel Worksheet:

The proportion defective is calculated by dividing the number of errors with the number of samples. For sample 1, the number of errors 4 is divided by 200 which give 0.02 as prop defective.
Hence, the fraction defective is shown in Table 1.
b)
To determine: The estimation for fraction defective when true fraction defective for the process is unknown.
Introduction: Quality is a measure of excellence or a state of being free from deficiencies, defects and important variations. It is obtained by consistent and strict commitment to certain standards to attain uniformity of a product to satisfy consumers’ requirement.
b)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Calculation of fraction defective:
The fraction defective is calculated when true fraction defective is unknown.
Total number of defective is calculated by adding the number of errors, (4+2+5+9) which accounts to 20
The fraction defective is calculated by dividing total number of defective with total number of observation which is 20 is divided with the product of 4 and 200 which is 0.025.
Hence, the fraction defective is 0.025.
c)
To determine: The estimate of mean and standard deviation of the sampling distribution of fraction defective for samples for the size.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
c)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Estimate of mean and standard deviation of the sampling distribution:
Mean = 0.025 (from equation (1))
The estimate for mean is shown in equation (1) and standard deviation is calculated by substituting the value which yields 0.011.
Hence, estimate of mean and standard deviation of the sampling distribution is 0.025 and 0.011.
d)
To determine: The control limits that would give an alpha risk of 0.03 for the process.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
d)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Control limits that would give an alpha risk of 0.03 for the process:
0.015 is in each tail and using z-factor table, value that corresponds to 0.5000 – 0.0150 is 0.4850 which is z = 2.17.
The UCL is calculated by adding 0.025 with the product of 2.17 and 0.011 which gives 0.0489 and LCL is calculated by subtracting 0.025 with the product of 2.17 and 0.011 which yields 0.0011.
Hence, the control limits that would give an alpha risk of 0.03 for the process are 0.0489 and 0.0011.
e)
To determine: The alpha risks that control limits 0.47 and 0.003 will provide.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
e)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Alpha risks that control limits 0.47 and 0.003 will provide:
The following equation z value can be calculated,
From z factor table, the probability value which corresponds to z = 2.00 is 0.4772, on each tail,
0.0228 is observed on each tail and doubling the value gives 0.0456 which is the alpha risk.
Hence, alpha risks that control limits 0.47 and 0.003 will provide is 0.0456
f)
To determine: Whether the process is in control when using 0.047 and 0.003.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has an upper control limit, and lower control which are used plot the time order.
f)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Calculation of fraction defective in each sample:
| n | 200 | |||
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
| Prop defective | 0.02 | 0.01 | 0.025 | 0.045 |
UCL = 0.047 & LCL = 0.003
Graph:
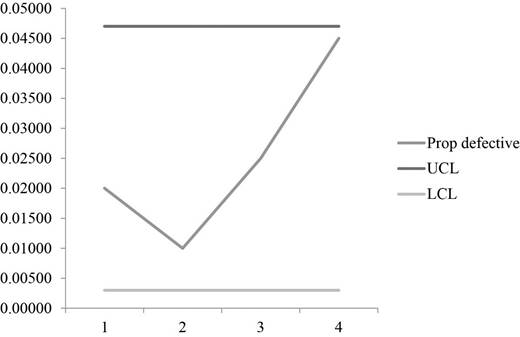
A graph is plotted using UCL, LCL and prop defective values which show that all the sample points are well within the control limits which makes the process to be in control.
Hence, the process is within control for the limits 0.047 & 0.003.
g)
To determine: The mean and standard deviation of the sampling distribution.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
g)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Long run fraction defective of the process is 0.02
Calculation of mean and standard deviation of the sampling distribution:
Fraction defective in each sample:
| n | 200 | |||
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
| Prop defective | 0.02 | 0.01 | 0.025 | 0.045 |
The mean is calculated by taking average for the proportion defective,
The values of the proportion defective are added and divided by 4 which give 0.02.
The standard deviation is calculated using the formula,
The standard deviation is calculated by substituting the values in the above formula and taking square root for the resultant value which yields 0.099.
Hence, mean and standard deviation of the sampling distribution is 0.02&0.0099.
h)
To construct: A control chart using two sigma control limits and check whether the process is in control.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
h)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Fraction defective in each sample:
| n | 200 | |||
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
| Prop defective | 0.02 | 0.01 | 0.025 | 0.045 |
Calculation of control limits:
The control limits are calculated using the above formula and substituting the values and taking square root gives the control limits of the UCL and LCL which are 0.0398 and 0.0002 respectively.
Graph:
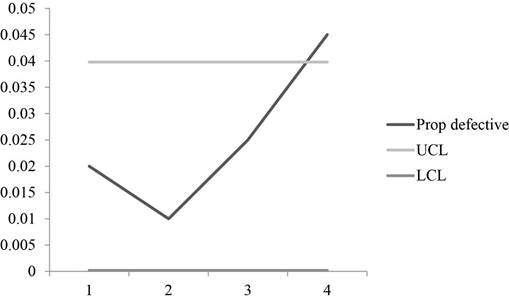
A graph is plotted using the fraction defective, UCL and LCL values which shows that one sample points is beyond the control region which makes the process to be out of control.
Hence, control chart is constructed using two-sigma control limits and the chart shows that the process is not in control.
Want to see more full solutions like this?
Chapter 10 Solutions
Operations Management (Comp. Instructor's Edition)
- Sarah Anderson, the Marketing Manager at Exeter Township's Cultural Center, is conducting research on the attendance history for cultural events in the area over the past ten years. The following data has been collected on the number of attendees who registered for events at the cultural center. Year Number of Attendees 1 700 2 248 3 633 4 458 5 1410 6 1588 7 1629 8 1301 9 1455 10 1989 You have been hired as a consultant to assist in implementing a forecasting system that utilizes various forecasting techniques to predict attendance for Year 11. a) Calculate the Three-Period Simple Moving Average b) Calculate the Three-Period Weighted Moving Average (weights: 50%, 30%, and 20%; use 50% for the most recent period, 30% for the next most recent, and 20% for the oldest) c) Apply Exponential Smoothing with the smoothing constant alpha = 0.2. d) Perform a Simple Linear Regression analysis and provide the adjusted…arrow_forwardRuby-Star Incorporated is considering two different vendors for one of its top-selling products which has an average weekly demand of 70 units and is valued at $90 per unit. Inbound shipments from vendor 1 will average 390 units with an average lead time (including ordering delays and transit time) of 4 weeks. Inbound shipments from vendor 2 will average 490 units with an average lead time of 2 weeksweeks. Ruby-Star operates 52 weeks per year; it carries a 4-week supply of inventory as safety stock and no anticipation inventory. Part 2 a. The average aggregate inventory value of the product if Ruby-Star used vendor 1 exclusively is $enter your response here.arrow_forwardSam's Pet Hotel operates 50 weeks per year, 6 days per week, and uses a continuous review inventory system. It purchases kitty litter for $13.00 per bag. The following information is available about these bags: > Demand 75 bags/week > Order cost = $52.00/order > Annual holding cost = 20 percent of cost > Desired cycle-service level = 80 percent >Lead time = 5 weeks (30 working days) > Standard deviation of weekly demand = 15 bags > Current on-hand inventory is 320 bags, with no open orders or backorders. a. Suppose that the weekly demand forecast of 75 bags is incorrect and actual demand averages only 50 bags per week. How much higher will total costs be, owing to the distorted EOQ caused by this forecast error? The costs will be $higher owing to the error in EOQ. (Enter your response rounded to two decimal places.)arrow_forward
- Yellow Press, Inc., buys paper in 1,500-pound rolls for printing. Annual demand is 2,250 rolls. The cost per roll is $625, and the annual holding cost is 20 percent of the cost. Each order costs $75. a. How many rolls should Yellow Press order at a time? Yellow Press should order rolls at a time. (Enter your response rounded to the nearest whole number.)arrow_forwardPlease help with only the one I circled! I solved the others :)arrow_forwardOsprey Sports stocks everything that a musky fisherman could want in the Great North Woods. A particular musky lure has been very popular with local fishermen as well as those who buy lures on the Internet from Osprey Sports. The cost to place orders with the supplier is $40/order; the demand averages 3 lures per day, with a standard deviation of 1 lure; and the inventory holding cost is $1.00/lure/year. The lead time form the supplier is 10 days, with a standard deviation of 2 days. It is important to maintain a 97 percent cycle-service level to properly balance service with inventory holding costs. Osprey Sports is open 350 days a year to allow the owners the opportunity to fish for muskies during the prime season. The owners want to use a continuous review inventory system for this item. Refer to the standard normal table for z-values. a. What order quantity should be used? lures. (Enter your response rounded to the nearest whole number.)arrow_forward
- In a P system, the lead time for a box of weed-killer is two weeks and the review period is one week. Demand during the protection interval averages 262 boxes, with a standard deviation of demand during the protection interval of 40 boxes. a. What is the cycle-service level when the target inventory is set at 350 boxes? Refer to the standard normal table as needed. The cycle-service level is ☐ %. (Enter your response rounded to two decimal places.)arrow_forwardOakwood Hospital is considering using ABC analysis to classify laboratory SKUs into three categories: those that will be delivered daily from their supplier (Class A items), those that will be controlled using a continuous review system (B items), and those that will be held in a two bin system (C items). The following table shows the annual dollar usage for a sample of eight SKUs. Fill in the blanks for annual dollar usage below. (Enter your responses rounded to the mearest whole number.) Annual SKU Unit Value Demand (units) Dollar Usage 1 $1.50 200 2 $0.02 120,000 $ 3 $1.00 40,000 $ 4 $0.02 1,200 5 $4.50 700 6 $0.20 60,000 7 $0.90 350 8 $0.45 80arrow_forwardA part is produced in lots of 1,000 units. It is assembled from 2 components worth $30 total. The value added in production (for labor and variable overhead) is $30 per unit, bringing total costs per completed unit to $60 The average lead time for the part is 7 weeks and annual demand is 3800 units, based on 50 business weeks per year. Part 2 a. How many units of the part are held, on average, in cycle inventory? enter your response here unitsarrow_forward
- assume the initial inventory has no holding cost in the first period and back orders are not permitted. Allocating production capacity to meet demand at a minimum cost using the transportation method. What is the total cost? ENTER your response is a whole number (answer is not $17,000. That was INCORRECT)arrow_forwardRegular Period Time Overtime Supply Available puewag Subcontract Forecast 40 15 15 40 2 35 40 28 15 15 20 15 22 65 60 Initial inventory Regular-time cost per unit Overtime cost per unit Subcontract cost per unit 20 units $100 $150 $200 Carrying cost per unit per month 84arrow_forwardassume that the initial inventory has no holding cost in the first period, and back orders are not permitted. Allocating production capacity to meet demand at a minimum cost using the transportation method. The total cost is? (enter as whole number)arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

