
Concept explainers
Usually, we do not walk or even stand on a lightweight boat or raft because of the danger of falling into the water. If you have ever stepped off a small boat onto a dock, however, you have probably noticed that the boat moves away from the dock as you step toward the dock or out of the boat. A heavy dog running on a long lightweight raft presents a similar situation. At first, the raft and the dog are at rest with respect to the water (Fig. P10.38A) so that
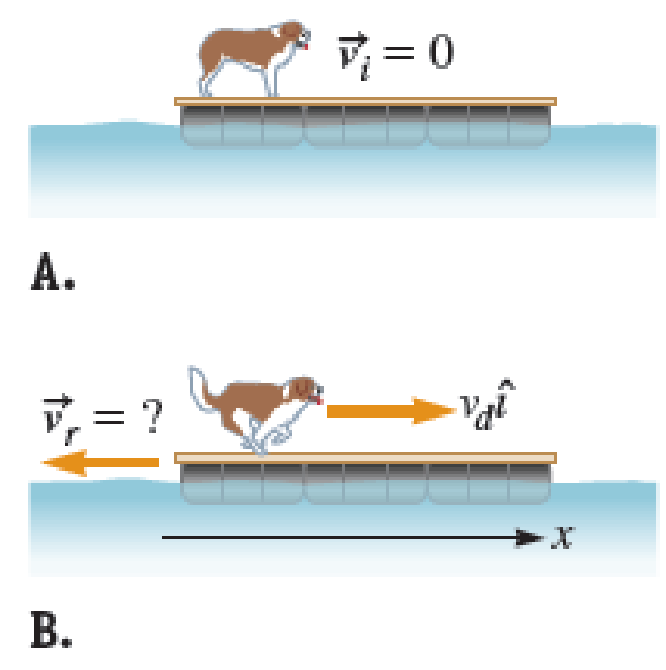
FIGURE P10.38
Trending nowThis is a popular solution!

Chapter 10 Solutions
Physics for Scientists and Engineers: Foundations and Connections
- In general it is best to conceptualize vectors as arrows in space, and then to make calculations with them using their components. (You must first specify a coordinate system in order to find the components of each arrow.) This problem gives you some practice with the components. Let vectors A = (1,0, -3), B = (-2, 5, 1), and C = (3,1,1). Calculate the following, and express your answers as ordered triplets of values separated by commas.arrow_forwardIn general it is best to conceptualize vectors as arrows in space, and then to make calculations with them using their components. (You must first specify a coordinate system in order to find the components of each arrow.) This problem gives you some practice with the components. Let vectors A = (1,0, −3), B = (-2, 5, 1), and C = (3,1,1). Calculate the following, and express your answers as ordered triplets of values separated by commas.arrow_forwardOnly Part C.) is necessaryarrow_forward
- Only Part B.) is necessaryarrow_forwardA (3.60 m) 30.0°- 70.0° x B (2.40 m)arrow_forwardIn general it is best to conceptualize vectors as arrows in space, and then to make calculations with them using their components. (You must first specify a coordinate system in order to find the components of each arrow.) This problem gives you some practice with the components. Let vectors A = (1,0, -3), B = (-2, 5, 1), and C = (3,1,1). Calculate the following, and express your answers as ordered triplets of values separated by commas.arrow_forward
- fine the magnitude of the vector product express in sq meters what direction is the vector product in -z or +zarrow_forward4) Three point charges of magnitude Q1 = +2.0 μC, Q2 = +3.0 μС, Q3 = = +4.0 μС are located at the corners of a triangle as shown in the figure below. Assume d = 20 cm. (a) Find the resultant force vector acting on Q3. (b) Find the magnitude and direction of the force. d Q3 60° d Q1 60° 60° Q2 darrow_forwardThree point charges of magnitudes Q₁ = +6.0 μС, Q₂ = −7.0 μС, Qз = −13.0 μC are placed on the x-axis at x = 0 cm, x = 40 cm, and x = 120 cm, respectively. What is the force on the Q3 due to the other two charges?arrow_forward
 Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





