
a.
The
| Year | Population ( in thousands) |
| 2012 | 19321 |
| 2013 | 19533 |
| 2014 | 19893 |
| 2015 | 20271 |
| 2016 | 20612 |
| 2017 | 20984 |
a.
Answer to Problem 53RE
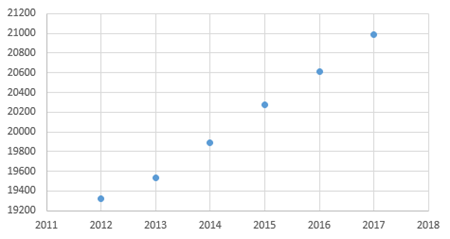
The obtained graph is defined as,
Explanation of Solution
Given Information:
The table is defined as,
| Year | Population ( in thousands) |
| 2012 | 19321 |
| 2013 | 19533 |
| 2014 | 19893 |
| 2015 | 20271 |
| 2016 | 20612 |
| 2017 | 20984 |
Consider the given table,
| Year | Population ( in thousands) |
| 2012 | 19321 |
| 2013 | 19533 |
| 2014 | 19893 |
| 2015 | 20271 |
| 2016 | 20612 |
| 2017 | 20984 |
Draw the points on the plane to make the scatter plot.

Therefore, the above graph is required scatter plot.
b.
To calculate: The slope of the secant line
b.
Answer to Problem 53RE
The slopes are
And, the function is not discontinues
Explanation of Solution
Given information:
The table is defined as,
| Year | Population ( in thousands) |
| 2012 | 19321 |
| 2013 | 19533 |
| 2014 | 19893 |
| 2015 | 20271 |
| 2016 | 20612 |
| 2017 | 20984 |
Formula Used:
If
Calculation:
Consider the given table,
The initial point
Now, find the slope of the point
Now, find the slope of the point
The
Now, find the slope of the point
The
Therefore, the obtained slopes are
c.
To calculate: The slope of the secant line
c.
Answer to Problem 53RE
The slopes are
Explanation of Solution
Given information:
The table is defined as,
| Year | Population ( in thousands) |
| 2012 | 19321 |
| 2013 | 19533 |
| 2014 | 19893 |
| 2015 | 20271 |
| 2016 | 20612 |
| 2017 | 20984 |
Formula Used:
If
Calculation:
Consider the given table,
The initial point
Now, find the slope of the point
Now, find the slope of the point
The
Now, find the slope of the point
The
Now, find the slope of the point
The
Now, find the slope of the point
The
Now, add all the averages and divide by number of average.
Therefore, the obtained average is
d.
To calculate: The instantaneous slope at 1 July 2013.
d.
Answer to Problem 53RE
The slopes are
Explanation of Solution
Given information:
The table is defined as,
| Year | Population ( in thousands) |
| 2012 | 19321 |
| 2013 | 19533 |
| 2014 | 19893 |
| 2015 | 20271 |
| 2016 | 20612 |
| 2017 | 20984 |
Formula Used:
If
Calculation:
Consider the given table,
The initial point
Now, find the slope at 1 July 2013.
Therefore, the obtained slope is 212 thousand in year.
e.
The reason that why linear growth may or may not be a bad assumption over longer periods of time.
e.
Answer to Problem 53RE
The linear asuumation is incorrect.
Explanation of Solution
Given information:
The table is defined as,
| Year | Population ( in thousands) |
| 2012 | 19321 |
| 2013 | 19533 |
| 2014 | 19893 |
| 2015 | 20271 |
| 2016 | 20612 |
| 2017 | 20984 |
Consider the given table,
As it can be observed that the slope between all the years is not same as calculated in previous part. For each year the slope is different this implies that the growth of the population in each year is different. The slope is increasing in each year.
And for the linear growth the slope should be same in each year. So it is not possible to calculate the correct estimates of the population in 2020 by using the linear equation. Thus, the linear model may be a bad assumption over the longer periods of time to calculate the population in any year.
Therefore, the linear model is incorrect.
Chapter 1 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- 2. Suppose f(x) = 3x² - 5x. Show all your work for the problems below.arrow_forwardwrite it down for better understanding pleasearrow_forward1. Suppose F(t) gives the temperature in degrees Fahrenheit t minutes after 1pm. With a complete sentence, interpret the equation F(10) 68. (Remember this means explaining the meaning of the equation without using any mathy vocabulary!) Include units. (3 points) =arrow_forward
- 2. Suppose f(x) = 3x² - 5x. Show all your work for the problems below. a. Evaluate f(-3). If you have multiple steps, be sure to connect your expressions with EQUALS SIGNS. (3 points)arrow_forward4c Consider the function f(x) = 10x + 4x5 - 4x³- 1. Enter the general antiderivative of f(x)arrow_forwardA tank contains 60 kg of salt and 2000 L of water. Pure water enters a tank at the rate 8 L/min. The solution is mixed and drains from the tank at the rate 11 L/min. Let y be the number of kg of salt in the tank after t minutes. The differential equation for this situation would be: dy dt y(0) =arrow_forward
- • • Let > be a potential for the vector field F = (−2 y³, −6 xy² − 4 z³, −12 yz² + 4 2). Then the value of sin((-1.63, 2.06, 0.57) – (0,0,0)) is - 0.336 -0.931 -0.587 0.440 0.902 0.607 -0.609 0.146arrow_forwardThe value of cos(4M) where M is the magnitude of the vector field with potential ƒ = e² sin(лy) cos(π²) at x = 1, y = 1/4, z = 1/3 is 0.602 -0.323 0.712 -0.816 0.781 0.102 0.075 0.013arrow_forwardThere is exactly number a and one number b such that the vector field F = conservative. For those values of a and b, the value of cos(a) + sin(b) is (3ay + z, 3ayz + 3x, −by² + x) is -0.961 -0.772 -1.645 0.057 -0.961 1.764 -0.457 0.201arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





