Chapter 1.2, Problem 6E

(a)

To determine

To find: The limit of $\underset{x\to \infty }{\lim }f(x)$

Answer to Problem 6E

The limit is 2.

Explanation of Solution

Given information: The function is $f(x)=\frac{2x-`1}{\left|x\right|-3}$

Graph:

The given function is:

  $f(x)=\frac{2x-`1}{\left|x\right|-3}$

The graph of the function $f(x)=\frac{2x-`1}{\left|x\right|-3}$ is shown below:

  

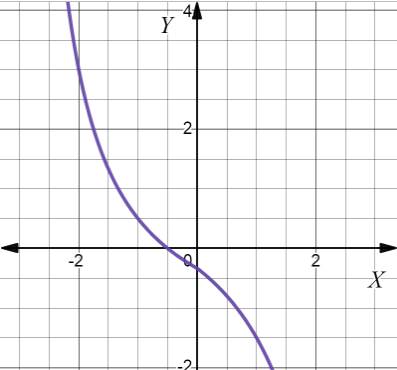
As the graph above,

  $\underset{x\to +\infty }{\lim }f(x)=2$

The table of values and $f(x)$ approaches that limit:

x	f(x)
1	-0.500000
10	2.714286
100	2.051546
1000	2.005015
10000	2.000500
100000	2.000050

With a graphing tool and a table, determine that the limit of $f(x)$ as $x$ approaches infinity equals 2.

(b)

To determine

To find: The limit of $\underset{x\to -\infty }{\lim }f(x)$

Answer to Problem 6E

The limit is -2.

Explanation of Solution

Given information: The function is $f(x)=\frac{2x-`1}{\left|x\right|-3}$

Graph:

The given function is:

  $f(x)=\frac{2x-`1}{\left|x\right|-3}$

The graph of the function $f(x)=\frac{2x-`1}{\left|x\right|-3}$ is shown below:

The horizontal dotted line is $y=-2$

  

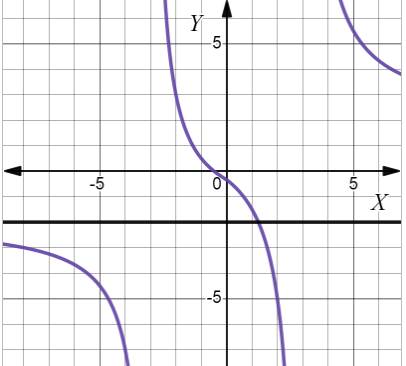
As the graph above,

  $\underset{x\to -\infty }{\lim }f(x)=-2$

The table of values and $f(x)$ approaches that limit:

x	f(x)
-1	1.500000
-10	-3.000000
-100	-2.072165
-1000	-2.007021
-10000	-2.000700
-100000	-2.000070

With a graphing tool and a table, determine that the limit of $f(x)$ as $x$ approaches infinity equals -2.

(c)

To determine

To find: The horizontal asymptote

Answer to Problem 6E

  $\begin{array}{c}y=-2\\ y=2\end{array}$

Are two horizontal asymptotes.

Explanation of Solution

Given information: The function is $f(x)=\frac{2x-`1}{\left|x\right|-3}$

Calculation:

The given function is:

  $f(x)=\frac{2x-`1}{\left|x\right|-3}$

From part a)

  $\underset{x\to +\infty }{\lim }f(x)=2$

From part b)

  $\underset{x\to -\infty }{\lim }f(x)=-2$

Therefore, $\begin{array}{c}y=-2\\ y=2\end{array}$ are two horizontal asymptotes.