
(a.)
To explain: Why limit is restricted to
(a.)
Answer to Problem 77E
From the figure it can be observed that the graph of the function lies between
Explanation of Solution
Given:
The given figure is shown below:
Consider the given graph.
It is known that an output value that a function approaches for the specified input values is referred to as a limit.
From the given figure it can be observed that the value of the function or the limit of the function when x approaching to 0 is depends only for the positive x values near zero. This is why limit is restricted to
(b.)
To Prove: The area of
(b.)
Explanation of Solution
Given:
The given figure is shown below:
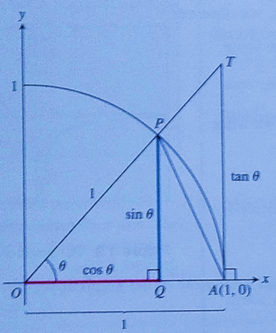
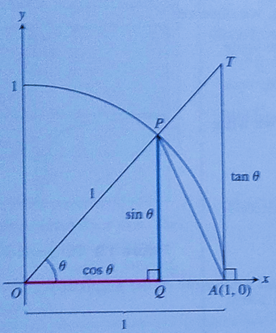
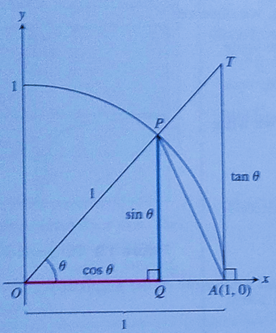
Concept used:
Area of triangle is:
Area of sector is:
Calculation:
Consider the given figure.
From the figure it can be observed that, in
Put
Consider the sector
From the figure it can be observed that, in sector
Use the area of the sector formula:
Consider the triangle
From the figure it can be observed that, in
Put
(c.)
To Prove: That
(c.)
Explanation of Solution
Given:
From part (b) The area of
The given figure is shown below:

Concept used:
In a right-angled triangle one of its angles is
Calculation:
Consider the given information.
The triangle given in the figure is right angle triangle and in a right angle triangle one angle is
Also, it is known that the area of
Now observe the value of
Also, from the figure it can be observed that
Therefore,
(d.)
To Prove: That
(d.)
Explanation of Solution
Given:
The given inequality is:
Concept used:
Domain of a function is the set of input values which a function can take.
Calculation:
Consider the given inequality.
Mulitiply each side of the inequality by 2.
Now divide each side by
(e.)
To Prove: That
(e.)
Explanation of Solution
Given:
The given inequality is:
Concept used:
Domain of a function is the set of input values which a function can take.
Calculation:
Consider the given inequality.
Taking reciprocal of the above inequality and change the direction of the inequlaity.
(f.)
To Prove:
(f.)
Explanation of Solution
Given:
The given limit is
Concept used:
The squeeze theorem states that if
Calculation:
Consider the given information.
From part (e) it is known that
Applying limit on each function.
Let
Thus,
Let
Thus,
Therefore, by the squeeze theorem
(g.)
To Prove: That
(g.)
Explanation of Solution
Given:
The given function is
Concept used:
A function is said to be even if
Calculation:
Consider the given function.
Replace
Since
(h.)
To Prove: That
(h.)
Explanation of Solution
Given:
From part (g) it is known that
Concept used:
The squeeze theorem states that if
Calculation:
Consider the given limit.
Take
Therefore,
(i.)
To Prove:
(i.)
Explanation of Solution
Given:
From part (f) and (h) it is known that
Concept used:
The limit of a function as it approaches from the left is referred to as the left-hand limit. The limit of a function as it approaches from the right-hand side is referred to as a right-hand limit.
Calculation:
Consider the given information.
From part (f) and (h) it is known that
If the function has both limits defined at a particular x value c and those values match, then the limit will exist and will be equal to the value of the one-sided limits.
Since the left- and right-hand limits are equal so
Therefore,
Chapter 1 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- Problem 11 (a) A tank is discharging water through an orifice at a depth of T meter below the surface of the water whose area is A m². The following are the values of a for the corresponding values of A: A 1.257 1.390 x 1.50 1.65 1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650 1.80 1.95 2.10 2.25 2.40 2.55 2.70 2.85 Using the formula -3.0 (0.018)T = dx. calculate T, the time in seconds for the level of the water to drop from 3.0 m to 1.5 m above the orifice. (b) The velocity of a train which starts from rest is given by the fol- lowing table, the time being reckoned in minutes from the start and the speed in km/hour: | † (minutes) |2|4 6 8 10 12 14 16 18 20 v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0 Estimate approximately the total distance ran in 20 minutes.arrow_forwardX Solve numerically: = 0,95 In xarrow_forwardX Solve numerically: = 0,95 In xarrow_forward
- Please as many detarrow_forward8–23. Sketching vector fields Sketch the following vector fieldsarrow_forward25-30. Normal and tangential components For the vector field F and curve C, complete the following: a. Determine the points (if any) along the curve C at which the vector field F is tangent to C. b. Determine the points (if any) along the curve C at which the vector field F is normal to C. c. Sketch C and a few representative vectors of F on C. 25. F = (2½³, 0); c = {(x, y); y − x² = 1} 26. F = x (23 - 212) ; C = {(x, y); y = x² = 1}) , 2 27. F(x, y); C = {(x, y): x² + y² = 4} 28. F = (y, x); C = {(x, y): x² + y² = 1} 29. F = (x, y); C = 30. F = (y, x); C = {(x, y): x = 1} {(x, y): x² + y² = 1}arrow_forward
- ٣/١ B msl kd 180 Ka, Sin (1) I sin () sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 G 5005 1000 s = 1000-950 Copper bosses 5kW Rotor input 5 0.05 : loo kw 6) 1 /0001 ined sove in peaper I need a detailed solution on paper please وه اذا ميريد شرح الكتب فقط ١٥٠ DC 7) rotor a ' (y+xlny + xe*)dx + (xsiny + xlnx + dy = 0. Q1// Find the solution of: ( 357arrow_forward۳/۱ R₂ = X2 2) slots per pole per phase 3/31 B. 180 msl Kas Sin (I) 1sin() sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30): 0.866 4) Rotating 5) Synchronous speeds 120×50 looo G 1000-950 1000 Copper losses 5kw Rotor input 5 loo kw 0.05 6) 1 اذا ميريد شرح الكتب فقط look 7) rotor DC ined sove in peaper I need a detailed solution on paper please 0 64 Find the general solution of the following equations: QI//y(4)-16y= 0. Find the general solution of the following equations: Q2ll yll-4y/ +13y=esinx.arrow_forwardR₂ = X2 2) slots per pole per phase = 3/31 B-180 60 msl kd Kas Sin () 2 I sin (6) sin(30) Sin (30) اذا مريد شرح الكتب بس 0 بالفراغ 3 Cos (30) 0.866 4) Rotating ined sove in peaper 5) Synchronous speed s 120×50 6 s = 1000-950 1000 Copper losses 5kw Rotor input 5 0.05 6) 1 loo kw اذا ميريد شرح الكتب فقط Look 7) rotov DC I need a detailed solution on paper please 0 64 Solve the following equations: 0 Q1// Find the solution of: ( y • with y(0) = 1. dx x²+y²arrow_forward
- R₂ = X2 2) slots per pole per phase = 3/3 1 B-180-60 msl Ka Sin (1) Isin () sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 s = 1000-950 1000 Copper losses 5kw Rotor input 5 6) 1 0.05 G 50105 loo kw اذا ميريد شرح الكتب فقط look 7) rotov DC ined sove in peaper I need a detailed solution on paper please 064 2- A hot ball (D=15 cm ) is cooled by forced air T.-30°C, the rate of heat transfer from the ball is 460.86 W. Take for the air -0.025 Wim °C and Nu=144.89, find the ball surface temperature a) 300 °C 16 b) 327 °C c) 376 °C d) None か = 750 01arrow_forwardDon't do 14. Please solve 19arrow_forwardPlease solve 14 and 15arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





