has a different lifespan in water at a 0.05 level of significance. Sunscreen A Sunscreen B Sunscreen C Sunscreen D 43 66 64 49 90 80 51 74 40 57 44 83 87 74 63 43 43 31 49 84 58 57 64 68 The hypotheses for this ANOVA test would be: Ho: HA = HB = µc = HD HA: At least one mean is different. (claim) a = 0.05 Complete the ANOVA table below: (round answers to 3 decimal places) df MS F p-value Between Within The decision of the test is to: reject Ho odo not reject Họ The final conclusion is:

Given Information :
A sunscreen company is attempting to improve upon their formula so that it lasts in water longer . They have 4 lead scientists who each came up with a different formulas . In order to see if there is a difference in the time the sunscreen lasts the CEO collects a random sample of each of the four sunscreens and the data is provided .
This example teaches you how to perform a single factor ANOVA (analysis of variance) in Excel. A single factor or one-way ANOVA is used to test the null hypothesis that the means of several populations are all equal.
State the hypothesis :
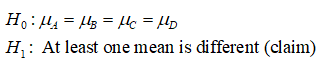
To perform a single factor ANOVA, execute the following steps.
1. On the Data tab, in the Analysis group, click Data Analysis.
2. Select Anova: Single Factor and click OK.
3. Click in the Input Range box and select the range of the given data.
4. Click in the Output Range box and select any empty cell.
5. Click OK.
Result:
Anova: Single Factor
| SUMMARY | ||||
| Groups | Count | Sum | Average | Variance |
| A | 6 | 361 | 60.16667 | 522.1667 |
| B | 6 | 365 | 60.83333 | 297.3667 |
| C | 6 | 335 | 55.83333 | 78.96667 |
| D | 6 | 401 | 66.83333 | 298.9667 |
| ANOVA | ||||||
| Source of Variation | SS | df | MS | F | P-value | F crit |
| Between Groups | 368.5 | 3 | 122.8333 | 0.410311 | 0.747339 | 3.098391 |
| Within Groups | 5987.333 | 20 | 299.3667 | |||
| Total | 6355.833 | 23 |
Step by step
Solved in 3 steps with 1 images









