Fundamentals of Statistics (5th Edition)
5th Edition
ISBN: 9780134508306
Author: Michael Sullivan III
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter B.6, Problem 21AYU
Lower Your Cholesterol Researcher Francisco Fuentes and his colleagues wanted to determine the most effective diet for reducing LDL cholesterol, the so-called “bad” cholesterol, among three diets: (1) a saturated-fat diet: 15% protein, 47% carbohydrates, and 38% fat (20% saturated fat, 12% monounsaturated fat, and 6% polyunsaturated fat); (2) the Mediterranean diet: 47% carbohydrates, and 38% fat (10% saturated fat, 22% monounsaturated fat, and 6% polyunsaturated fat); and (3) the US National Cholesterol Education Program or NCEP-1 Diet: 10% saturated fat, 12% monounsaturated fat, and 6% polyunsaturated fat. Participants in the study were shown to have the same levels of LDL cholesterol before the study and were randomly assigned to one of the three diets, or treatment groups. After 28 days, their LDL cholesterol levels were recorded. The data in the following table are based on this study.
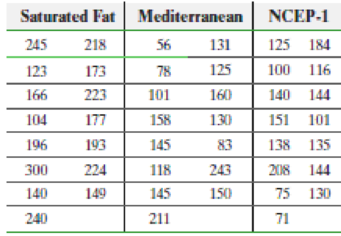
- (a) Why is this study a completely randomized design?
- (b) What is the response variable? What is the explanatory variable that is controlled and set at three levels?
- (c) The participants were randomly assigned to one of three treatment groups. What is the purpose of randomization in this study?
- (d) State the null and alternative hypotheses.
- (e) Verify that the requirements to use the one-way ANOVA procedure are satisfied. Normal probability plots indicate that the sample data come from normal populations.
- (f) Are the
mean LDL cholesterol levels different at the α = 0.05 level of significance? - (g) Draw boxplots of the LDL cholesterol levels for the three groups to support the analytic results obtained in part (f).
Expert Solution & Answer
Learn your wayIncludes step-by-step video
schedule14:29
Students have asked these similar questions
May I know how to solve a) and d)?
thank you
You get a job as the manager of a popular ice cream store in your hometown. One of your first concerns is determining how much ice cream you should stock to meet the demands of your customers. You suspect that the number of customers buying ice cream probably depends on several factors.
In looking through company files, you discover that the former manager collected considerable data. Last summer, a typical week produced the following data:
Day
Temperature (degrees Fahrenheit)
Number of Transactions
Gross Receipts (in dollars)
Monday
78
238
3014
Tuesday
73
194
2842
Wednesday
70
172
2141
Thursday
75
185
2235
Friday
83
270
4505
Saturday
89
320
5021
Sunday
94
280
4442
On the graph below, the temperature is graphed on the x axis and the number of transactions is graphed on the y axis.
Investigate the relationship between the temperature and the gross receipts. On the grid below, graph…
Some commercial airlines recirculate about half the air in the cabin during flights as a way to improve fuel efficiency. Other airlines make a policy of NOT recirculating the air and instead, have fresh air from the atmosphere constantly being inserted into the cabin with the “old” air being pumped out of the plane.
A total of 1100 passengers flying from San Francisco to Denver were used for an experiment. After their flight, they were each given a list of symptoms associated with the common cold. They were asked to report if they experienced cold symptoms within 24 hours of the flight landing.
Of the 517 passengers who flew on planes that recirculate the air, 108 reported post-flight cold symptoms. Of the 583 passengers who flew on airlines that do not use recirculation in the cabin, 110 reported symptoms.
Suppose now that we want to use the recirculation of air data to explore “Goal #2”, which is to resolve a hypothesis test about .
a) If we want to resolve this hypothesis…
Chapter B.6 Solutions
Fundamentals of Statistics (5th Edition)
Ch. B.6 - The acronym ANOVA stands for __________ __...Ch. B.6 - True or False: To perform a one-way ANOVA, the...Ch. B.6 - True or False: To perform a one-way ANOVA, the...Ch. B.6 - The variability among the sample means is called...Ch. B.6 - The variability within each treatment group, which...Ch. B.6 - True or False: The F-test statistic is F0=MSTMSE.Ch. B.6 - In Problems 7 and 8, fill in the ANOVA table. 7.Ch. B.6 - In Problems 7 and 8, fill in the ANOVA table. 8.Ch. B.6 - In Problems 9 and 10, determine the F-test...Ch. B.6 - In Problems 9 and 10, determine the F-test...
Ch. B.6 - NW 11. The following data represent a simple...Ch. B.6 - The following data represent a simple random...Ch. B.6 - NW 13. Corn Production The data in the table...Ch. B.6 - Soybean Yield The data in the table represent the...Ch. B.6 - Which Delivery Method Is Best? At a community...Ch. B.6 - Births by Day of Week An obstetrician knew that...Ch. B.6 - Rates of Return A stock analyst wondered whether...Ch. B.6 - Reaction Time In an online psychology experiment...Ch. B.6 - Car-Buying Discrimination To determine if there is...Ch. B.6 - Crash Data The Insurance Institute for Highway...Ch. B.6 - Lower Your Cholesterol Researcher Francisco...Ch. B.6 - pH in Rain An environmentalist wanted to determine...Ch. B.6 - Age and Politics Do peoples political philosophy...Ch. B.6 - Concrete Strength An engineer wants to know if the...Ch. B.6 - Analyzing Journal Article Results Researchers...Ch. B.6 - Prob. 27AYUCh. B.6 - Diversity and pH The following data represent the...Ch. B.6 - Another E-Cig Study In a study of adult smokers...Ch. B.6 - What are the requirements to perform a one-way...Ch. B.6 - What is the mean square due to treatment estimate...Ch. B.6 - Why does a large value of the F statistic provide...Ch. B.6 - In a one-way ANOVA, explain what it means to...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Constructing Confidence Intervals In Exercises 13 and 14, construct a 99% confidence interval for the populatio...
Elementary Statistics: Picturing the World (7th Edition)
House prices This chapter has considered many aspects of regression analysis. Let’s consider several of them at...
Statistics: The Art and Science of Learning from Data (4th Edition)
1. Standard Tests Standard tests, such as the SAT or ACT or MCAT, tend to make extensive use of multiple-choice...
Elementary Statistics (13th Edition)
Heights Refer to the dotplot in the previous question. a. What is the height of a woman with a z-score of -1? b...
Introductory Statistics (2nd Edition)
A father rates his daughter as a 2 on a 7-point scale (from 1 to 7) of crankiness. In this example, (a) what is...
Statistics for Psychology
An investment analyst has tracked a certain blue-chip stock for the past six months and found that on any given...
An Introduction to Mathematical Statistics and Its Applications (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Cholesterol Cholesterol in human blood is necessary, but too much can lead to health problems. There are three main types of cholesterol: HDL (high-density lipoproteins), LDL (low-density lipoproteins), and VLDL (very low-density lipoproteins). HDL is considered “good” cholesterol; LDL and VLDL are considered “bad” cholesterol. A standard fasting cholesterol blood test measures total cholesterol, HDL cholesterol, and triglycerides. These numbers are used to estimate LDL and VLDL, which are difficult to measure directly. Your doctor recommends that your combined LDL/VLDL cholesterol level be less than 130 milligrams per deciliter, your HDL cholesterol level be at least 60 milligrams per deciliter, and your total cholesterol level be no more than 200 milligrams per deciliter. (a) Write a system of linear inequalities for the recommended cholesterol levels. Let x represent the HDL cholesterol level, and let y represent the combined LDL VLDL cholesterol level. (b) Graph the system of inequalities from part (a). Label any vertices of the solution region. (c) Is the following set of cholesterol levels within the recommendations? Explain. LDL/VLDL: 120 milligrams per deciliter HDL: 90 milligrams per deciliter Total: 210 milligrams per deciliter (d) Give an example of cholesterol levels in which the LDL/VLDL cholesterol level is too high but the HDL cholesterol level is acceptable. (e) Another recommendation is that the ratio of total cholesterol to HDL cholesterol be less than 4 (that is, less than 4 to 1). Identify a point in the solution region from part (b) that meets this recommendation, and explain why it meets the recommendation.arrow_forwardIn a study of exhaust emissions from school buses, the pollution intake by passengers was determined for a sample of nine school buses used in the Southern California Air Basin. The pollution intake is the amount of exhaust emissions, in grams per person per million grams emitted, that would be inhaled while traveling on the bus during its usual 18-mile18-mile trip on congested freeways from South Central LA to a magnet school in West LA. (In comparison, a city of 11 million people will inhale a total of about 1212 grams of exhaust per million grams emitted.) The amounts for the nine buses when driven with the windows open are given in the table. 1.15 0.33 0.40 0.33 1.35 0.38 0.25 0.40 0.35 A good way to judge the effect of outliers is to do your analysis twice, once with the outliers and a second time without them. Give the 90%90% confidence interval with all the data for the mean pollution intake among all school buses used in the Southern California Air Basin that…arrow_forwardThe sales manager of a large automotive parts distributor wants to estimate the total annual sales for each of the company’s regions. Three factors appear to be related to regional sales: the number of retail outlets in the region, the total personal income of the region, and the number of cars registered in the region. The following table shows the data for 10 regions that were gathered for last year sales. The excel data file for this problem is:final exam question 6B spring 2021.xlsx Region Annual sales ($ million) Number of retail outlets Number of automobiles registered (million) Personal income ($ billion) 1 37.702 1,739 9.27 85.4 2 24.196 1,221 5.86 60.7 3 32.055 1,846 8.81 68.1 4 3.611 120 4.81 20.1 5 17.625 1,096 10.31 33.8 6 45.919 2,290 11.62 95.1 7 29.600 1,687 8.96 69.3 8 8.114 241 6.28 16.5 9 20.116 649 7.77 34.9 10 12.994 1,427 10.92…arrow_forward
- A manufacturing company is analyzing its accident record. The accidents fall intotwo categories: Minor—dealt with by first aider: Average cost k50 Major—hospital required. Average cost k1,000The company has 1,000 employees, of which 180 are office staff and the restwork in the factory.The analysis shows that 10% of employees have an accident each year and 20%of accidents are major. It is assumed that an employee has more than oneaccident in a year.(i) Determine the expected total cost of accidents in a year. On further analysis it is discovered that a member of office staff has half theprobability of having an accident relative those in the factory.(ii)Show that the probability that a given a member of office staff has anaccident in a year is 0.0549. (iii) Determine the probability that a randomly chosen employee who has hadan accident is office staffarrow_forwardA study shows that 80% of the population was vaccinated against the Venusian flu but 2% of the vaccinated population got the flu anyway. If 10% of the total population got this flu, what percent of the population either got the vaccine or got the disease?arrow_forwardMaple syrup is a non-negligible nutritional source of manganese. It is made from the sap of two species of maple: the sugar maple and the black maple. To see if there is a significant difference between the manganese content of these two species of maple, we measured the manganese content (in mg per 100g syrup) for a sample of sugar maples and a sample of black maples. The data is summarized by the Minitab output below: Two-sample T for Sugar Maple Black Maple group N Mean St Dev SE Mean Sugar Maple 20 Black Maple 12 3.55 0.29 Find: (i) a point estimate for ₁-2, where ₁ and 2 are the average manganese contents of the sugar maple, respectively the black maple; (ii) the standard error of X₁ - X₂. A) (i) -0.07; (ii) 0.101 C) (i) -0.26; (ii) 0.097 E) (i) -0.07; (ii) 0.035 3.29 0.22 0.049 0.084 B) (i) -0.26; (ii) 0.188 D) (i) -0.26; (ii) 0.101arrow_forward
- As humans we consume food. The body extracts good things such as proteins and vitamins and throws away waste. A typical waste product is uric acid. High levels of uric acid can be an indication of conditions such as gout, kidney disease, and cancer. For females a high level of uric acid is 6 mg/dL or more and for males a high level of uric acid is 7 mg/dL or more. Suppose, over a period of months, an adult male was given 6 blood tests for uric acid. The results of each blood test are shown below. results 9.48 11.1 8.58 11.4 10.34 11.58 The distribution of uric acid in healthy adult males is normally distributed with known population standard deviation, σ=1.94σ=1.94 mg/dl.Find a 95% confidence interval for the population mean of uric acid in this adult male's blood. Assume the sample of blood tests were given in a way that's equivalent to a simple random sample. (Round your answers to two decimal places.)margin of error __ mg/dL lower limit ___ mg/dL upper limit ___ mg/dLarrow_forwardAs humans we consume food. The body extracts good things such as proteins and vitamins and throws away waste. A typical waste product is uric acid. High levels of uric acid can be an indication of conditions such as gout, kidney disease, and cancer. For females a high level of uric acid is 6 mg/dL or more and for males a high level of uric acid is 7 mg/dL or more. Suppose, over a period of months, an adult female was given 10 blood tests for uric acid. The results of each blood test are shown below. Pisces for Tutoring BVC Student esources results 2.52 4.15 5.91 7.55 7.77 5.4 4.37 3.22 3.48 3.13 hat pogle Drive The distribution of uric acid in healthy adult females is normally distributed with known population standard deviation, o = 2.15 mg/dl. Find a 95% confidence interval for the population mean of uric acid in this adult female's blood. Assume the sample of blood tests were given in a way that's equivalent to a simple random sample. (Round your answers to two decimal places.)…arrow_forwardAs humans we consume food. The body extracts good things such as proteins and vitamins and throws away waste. A typical waste product is uric acid. High levels of uric acid can be an indication of conditions such as gout, kidney disease, and cancer. For females a high level of uric acid is 6 mg/dL or more and for males a high level of uric acid is 7 mg/dL or more. Suppose, over a period of months, an adult male has taken 8 blood test for uric acid. The results of the test are shown below. results 5.94 5.79 4.21 6.59 4.59 3.33 5.27 3.27 The distribution of uric acid in healthy adult males is normally distributed.Find a 95% confidence interval for the population mean of uric acid in this adult male's blood. (Round your answers to two decimal places.)margin of error mg/dLlower limit mg/dLupper limit mg/dLarrow_forward
- As humans we consume food. The body extracts good things such as proteins and vitamins and throws away waste. A typical waste product is uric acid. High levels of uric acid can be an indication of conditions such as gout, kidney disease, and cancer. For females a high level of uric acid is 6 mg/dL or more and for males a high level of uric acid is 7 mg/dL or more. Suppose, over a period of months, an adult male was given 9 blood tests for uric acid. The results of each blood test are shown below. results 10.24 10.1 11.19 11.1 9.34 9.58 9.63 10.59 9.58 The distribution of uric acid in healthy adult males is normally distributed with known population standard deviation, σ=1.15σ=1.15 mg/dl.Find a 95% confidence interval for the population mean of uric acid in this adult male's blood. Assume the sample of blood tests were given in a way that's equivalent to a simple random sample. (Round your answers to two decimal places.) margin of error ? mg/dLlower limit? mg/dLupper limit?…arrow_forwardAs humans we consume food. The body extracts good things such as proteins and vitamins and throws away waste. A typical waste product is uric acid. High levels of uric acid can be an indication of conditions such as gout, kidney disease, and cancer. For females a high level of uric acid is 6 mg/dL or more and for males a high level of uric acid is 7 mg/dL or more. Suppose, over a period of months, an adult female was given 5 blood tests for uric acid. The results of each blood test are shown below. results 6.75 6.68 12.07 10.29 6.68 The distribution of uric acid in healthy adult females is normally distributed with known population standard deviation, σ=2.09σ=2.09 mg/dl.Find a 95% confidence interval for the population mean of uric acid in this adult female's blood. Assume the sample of blood tests were given in a way that's equivalent to a simple random sample. (Round your answers to two decimal places.)margin of error mg/dLlower limit mg/dLupper limit mg/dLDoes this…arrow_forwardAs humans we consume food. The body extracts good things such as proteins and vitamins and throws away waste. A typical waste product is uric acid. High levels of uric acid can be an indication of conditions such as gout, kidney disease, and cancer. For females a high level of uric acid is 6 mg/dL or more and for males a high level of uric acid is 7 mg/dL or more. Suppose, over a period of months, an adult male has taken 8 blood test for uric acid. The results of the test are shown below. results 1.54 7.96 7.51 4.84 1.87 6.53 5.99 5.03 The distribution of uric acid in healthy adult males is normally distributed.Find a 95% confidence interval for the population mean of uric acid in this adult male's blood. (Round your answers to two decimal places.)margin of error mg/dL lower limit mg/dL upper limit mg/dLDoes this confidence interval suggest that this adult male has a high level of uric acid? No, since the interval is contained within the acceptable range levels. Yes, since the…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Propositional Logic, Propositional Variables & Compound Propositions; Author: Neso Academy;https://www.youtube.com/watch?v=Ib5njCwNMdk;License: Standard YouTube License, CC-BY
Propositional Logic - Discrete math; Author: Charles Edeki - Math Computer Science Programming;https://www.youtube.com/watch?v=rL_8y2v1Guw;License: Standard YouTube License, CC-BY
DM-12-Propositional Logic-Basics; Author: GATEBOOK VIDEO LECTURES;https://www.youtube.com/watch?v=pzUBrJLIESU;License: Standard Youtube License
Lecture 1 - Propositional Logic; Author: nptelhrd;https://www.youtube.com/watch?v=xlUFkMKSB3Y;License: Standard YouTube License, CC-BY
MFCS unit-1 || Part:1 || JNTU || Well formed formula || propositional calculus || truth tables; Author: Learn with Smily;https://www.youtube.com/watch?v=XV15Q4mCcHc;License: Standard YouTube License, CC-BY