
Express the result of each of these complex-number manipulations in polar form, using six significant figures just for the pure joy of calculating (a) 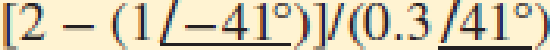 ; (b)
; (b) 
 ; (c)
; (c)  .
.
(a)
The polar form of the given complex number.
Answer to Problem 7P
The polar form of the given complex number is
Explanation of Solution
Given data:
The given complex number
Calculation:
The polar form of the function is given as,
Here,
The rectangular form of any function given in the form of
Here,
Substitute
Substitute
Substitute
Substitute
Conclusion:
Therefore, the polar form of the given complex number is
(b)
The polar form of the given complex number.
Answer to Problem 7P
The polar form of the given complex number is
Explanation of Solution
Given data:
The given complex number
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
Therefore, the polar form of the given complex number is
(c)
The polar form of the given complex number.
Answer to Problem 7P
The polar form of the given complex number is
Explanation of Solution
Given data:
The given complex number
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
Therefore, the polar form of the given complex number is
Want to see more full solutions like this?
Chapter A5 Solutions
Loose Leaf for Engineering Circuit Analysis Format: Loose-leaf
Additional Engineering Textbook Solutions
Starting Out with C++ from Control Structures to Objects (9th Edition)
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Mechanics of Materials (10th Edition)
SURVEY OF OPERATING SYSTEMS
Vector Mechanics for Engineers: Statics
Fluid Mechanics: Fundamentals and Applications
- They are one quearrow_forwardO Draw the four possible negative feedback contigurations of an op-amp. Write the input and output impedances of these configurations in ideal cases. 5arrow_forwardE9.6 Determine the average power absorbed by the 4-2 and 3-2 resistors in Fig. E9.6. 302 j20 Figure E9.3 4Ω ww Figure E9.6 12/0° V j30 -j2 N 13/10° A (+60° V (OEFarrow_forward
- -160 For the P-channel JFET given in the following figure, the IDSS = 2MA a) Determine IDQ and VSDQ b) Determine the source-follower circuit transistor parameters are: Vp = +1,75 V, and λ=0. Small-signal voltage gain, Av = So VDD = 10V R₁ = 90kr Rs =5k CC1 WW R₂ = 110kn 50 C02 BL = 10 kr GNDarrow_forwardNeed a solarrow_forwardI need a drawing on how to connect the function generator, oscilliscope, and both multimeters. It is hard for me to follow text instructions. The function generator has a postive,common and negative. The oscilliscope has chanell A and B, both channels have a postive and a negative. I know you can provide text instruction but a little sketch would be very helpful thank you.arrow_forward
- Don't use ai to answer I will report you answerarrow_forwardQ1/ A three phase, 500 kVA, 6600 V, 50 Hz, 6 pole, star connected synchronous motor has synchronous impedance of J 70 ohm per phase at its normal rating, the motor is excited to give unity power factor at the input terminals. Find a) The rated current and power factor. b) The emf behind the synchronous impedance. c) The developed torque. d) The pull out torque. e) The increase in excitation which will just permit an increase of 30% of rated torque before pulling out of synchronism. (45 M.)arrow_forwardcan you fin Vds and Vgs of all transistors and specify te operating region off all transistors and prove it. 58V 5.8 V 1.8V M2 0.9V 22222 と A 4852 m 3 01 A Voy = 0.2 V V4)=0.SV λ=0.1 V-1arrow_forward
 EBK ELECTRICAL WIRING RESIDENTIALElectrical EngineeringISBN:9781337516549Author:SimmonsPublisher:CENGAGE LEARNING - CONSIGNMENT
EBK ELECTRICAL WIRING RESIDENTIALElectrical EngineeringISBN:9781337516549Author:SimmonsPublisher:CENGAGE LEARNING - CONSIGNMENT
