
Concept explainers
For the beam and loading shown, determine (a) the slope at point B, (b) the deflection at point D. Use E = 200 GPa.

Fig. P9.128
The magnitude
Answer to Problem 146P
The magnitude
Explanation of Solution
Given information:
The section of the beam is
The young’s modulus of steel is
Calculation:
Show the free body diagram of the beam as in Figure 1.
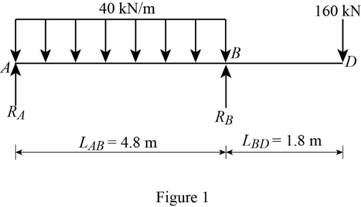
Calculate the vertical reaction at point A by taking moment about point B.
Refer Appendix C “Properties of rolled steel shape (SI units)” for moment of inertia of section
Calculate the value (EI):
Substitute
Calculate the moment due to the reaction at A:
Substitute
Calculate the
Substitute
Show the
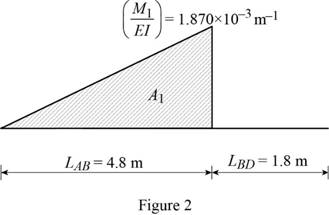
Calculate the area
Substitute
Calculate the moment due UDL:
Substitute
Calculate the
Substitute
Show the
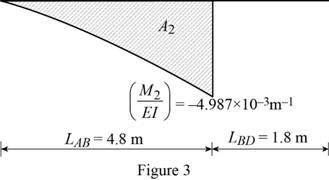
Calculate the area
Substitute
Calculate the moment due to the point load at D as below:
Substitute
Calculate the
Substitute
Show the
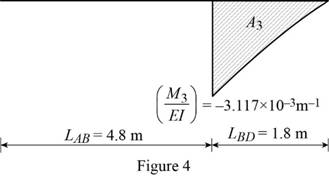
Calculate the area
Substitute
Calculate the tangential deviation of B with respect to A using the relation:
Substitute
Calculate the slope
Substitute
Let point K is the maximum deflection.
Calculate the moment due to the reaction at A as below:
Substitute
Calculate the
Substitute
Calculate the moment due UDL:
Calculate the
Substitute
Show the
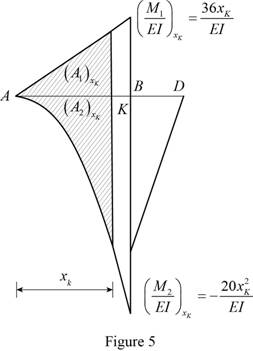
Calculate the area
Substitute
Calculate the area
Substitute
Calculate the slope
Substitute
Differentiate the Equation (1).
Solve the value
Iteration 1:
Substitute 3 for
Substitute 3 for
Iteration 2:
Calculate the value
Substitute 3 for
Similarly calculate the value
| f | ||
| 3 | 28.08 | -72 |
| 3.39 | -6.78 | -107.8 |
| 3.327 | -0.188 | -101.6 |
| 3.3251 | 0.005 | -101.42 |
| 3.32514 | 0.0001 |
The value of
Calculate the slope at the end A related to the point K
Substitute
Calculate the magnitude
Substitute
Thus, the magnitude
Want to see more full solutions like this?
Chapter 9 Solutions
Mechanics of Materials, 7th Edition
- (read image) (answer given)arrow_forwardA cylinder and a disk are used as pulleys, as shown in the figure. Using the data given in the figure, if a body of mass m = 3 kg is released from rest after falling a height h 1.5 m, find: a) The velocity of the body. b) The angular velocity of the disk. c) The number of revolutions the cylinder has made. T₁ F Rd = 0.2 m md = 2 kg T T₂1 Rc = 0.4 m mc = 5 kg ☐ m = 3 kgarrow_forward(read image) (answer given)arrow_forward
- 11-5. Compute all the dimensional changes for the steel bar when subjected to the loads shown. The proportional limit of the steel is 230 MPa. 265 kN 100 mm 600 kN 25 mm thickness X Z 600 kN 450 mm E=207×103 MPa; μ= 0.25 265 kNarrow_forwardT₁ F Rd = 0.2 m md = 2 kg T₂ Tz1 Rc = 0.4 m mc = 5 kg m = 3 kgarrow_forward2. Find a basis of solutions by the Frobenius method. Try to identify the series as expansions of known functions. (x + 2)²y" + (x + 2)y' - y = 0 ; Hint: Let: z = x+2arrow_forward
- 1. Find a power series solution in powers of x. y" - y' + x²y = 0arrow_forward3. Find a basis of solutions by the Frobenius method. Try to identify the series as expansions of known functions. 8x2y" +10xy' + (x 1)y = 0 -arrow_forwardHello I was going over the solution for this probem and I'm a bit confused on the last part. Can you please explain to me 1^4 was used for the Co of the tubular cross section? Thank you!arrow_forward
- Blood (HD = 0.45 in large diameter tubes) is forced through hollow fiber tubes that are 20 µm in diameter.Equating the volumetric flowrate expressions from (1) assuming marginal zone theory and (2) using an apparentviscosity for the blood, estimate the marginal zone thickness at this diameter. The viscosity of plasma is 1.2 cParrow_forwardQ2: Find the shear load on bolt A for the connection shown in Figure 2. Dimensions are in mm Fig. 2 24 0-0 0-0 A 180kN (10 Markarrow_forwarddetermine the direction and magnitude of angular velocity ω3 of link CD in the four-bar linkage using the relative velocity graphical methodarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





