
International Edition---engineering Mechanics: Statics, 4th Edition
4th Edition
ISBN: 9781305501607
Author: Andrew Pytel And Jaan Kiusalaas
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
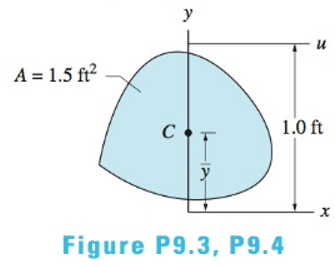
Chapter 9, Problem 9.3P
The moments of inertia of the plane region about the x- and u-axes are
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
3-15. A small fixed tube is shaped in the form of a vertical helix of radius a
and helix angle y, that is, the tube always makes an angle y with the horizontal.
A particle of mass m slides down the tube under the action of gravity. If there is
a coefficient of friction μ between the tube and the particle, what is the steady-state
speed of the particle? Let y
γ
30° and assume that µ < 1/√3.
The plate is moving at 0.6 mm/s when the force applied to the plate is 4mN. If the surface area of the plate in contact with the liquid is 0.5 m^2, deterimine the approximate viscosity of the liquid, assuming that the velocity distribution is linear.
3-9. Given that the force acting on a particle has the following components:
Fx = −x + y, Fy = x − y + y², F₂ = 0. Solve for the potential energy V.
-
Chapter 9 Solutions
International Edition---engineering Mechanics: Statics, 4th Edition
Ch. 9 - Compute the moment of inertia of the shaded region...Ch. 9 - The properties of the plane region are...Ch. 9 - The moments of inertia of the plane region about...Ch. 9 - The moment of inertia of the plane region about...Ch. 9 - Using integration, find the moment of inertia and...Ch. 9 - Use integration to determine the moment of inertia...Ch. 9 - Determine Ix and Iy for the plane region using...Ch. 9 - Using integration, compute the polar moment of...Ch. 9 - Use integration to compute Ix and Iy for the...Ch. 9 - By integration, determine the moments of inertia...
Ch. 9 - Compute the moment of inertia about the x-axis for...Ch. 9 - By integration, find the moment of inertia about...Ch. 9 - Figure (a) shows the cross section of a column...Ch. 9 - Compute the dimensions of the rectangle shown in...Ch. 9 - Compute Ix and Iy for the W867 shape dimensioned...Ch. 9 - Figure (a) shows the cross-sectional dimensions...Ch. 9 - A W867 section is joined to a C1020 section to...Ch. 9 - Compute Ix and Iy for the region shown.Ch. 9 - Prob. 9.19PCh. 9 - Calculate Ix for the shaded region, knowing that...Ch. 9 - Compute Iy for the region shown, given that...Ch. 9 - Prob. 9.22PCh. 9 - Prob. 9.23PCh. 9 - Determine Ix for the triangular region shown.Ch. 9 - Determine the distance h for which the moment of...Ch. 9 - A circular region of radius R/2 is cut out from...Ch. 9 - Prob. 9.27PCh. 9 - Determine the ratio a/b for which Ix=Iy for the...Ch. 9 - As a round log passes through a sawmill, two slabs...Ch. 9 - Prob. 9.30PCh. 9 - By numerical integration, compute the moments of...Ch. 9 - Use numerical integration to compute the moments...Ch. 9 - The plane region A is submerged in a fluid of...Ch. 9 - Use integration to verify the formula given in...Ch. 9 - For the quarter circle in Table 9.2, verify the...Ch. 9 - Determine the product of inertia with respect to...Ch. 9 - The product of inertia of triangle (a) with...Ch. 9 - Prob. 9.38PCh. 9 - For the region shown, Ixy=320103mm4 and Iuv=0....Ch. 9 - Prob. 9.40PCh. 9 - Calculate the product of inertia with respect to...Ch. 9 - Prob. 9.42PCh. 9 - Prob. 9.43PCh. 9 - The figure shows the cross section of a standard...Ch. 9 - Prob. 9.45PCh. 9 - Prob. 9.46PCh. 9 - Prob. 9.47PCh. 9 - Use numerical integration to compute the product...Ch. 9 - Determine the dimension b of the square cutout so...Ch. 9 - For the rectangular region, determine (a) the...Ch. 9 - Prob. 9.51PCh. 9 - Prob. 9.52PCh. 9 - Prob. 9.53PCh. 9 - Prob. 9.54PCh. 9 - Prob. 9.55PCh. 9 - The u- and v-axes are the principal axes of the...Ch. 9 - The x- and y-axes are the principal axes for the...Ch. 9 - Prob. 9.58PCh. 9 - The inertial properties of the region shown with...Ch. 9 - Determine Iu for the inverted T-section shown....Ch. 9 - Using Ix and Iu from Table 9.2, determine the...Ch. 9 - Show that every axis passing through the centroid...Ch. 9 - Prob. 9.63PCh. 9 - The L806010-mm structural angle has the following...Ch. 9 - Compute the principal centroidal moments of...Ch. 9 - Prob. 9.66PCh. 9 - Determine the principal axes and the principal...Ch. 9 - Compute the principal centroidal moments of...Ch. 9 - Find the moments and the product of inertia of the...Ch. 9 - Determine the moments and product of inertia of...Ch. 9 - Find the principal moments of inertia and the...Ch. 9 - Determine the moments and product of inertia of...Ch. 9 - Prob. 9.73PCh. 9 - Prob. 9.74PCh. 9 - The u- and v-axes are the principal axes of the...Ch. 9 - The x- and y-axes are the principal axes for the...Ch. 9 - Prob. 9.77PCh. 9 - The L806010-mm structural angle has the following...Ch. 9 - Prob. 9.79RPCh. 9 - Prob. 9.80RPCh. 9 - By integration, show that the product of inertia...Ch. 9 - Compute Ix and Iy for the shaded region.Ch. 9 - Using integration, evaluate the moments of inertia...Ch. 9 - The inertial properties at point 0 for a plane...Ch. 9 - Compute Ix and Iy for the shaded region.Ch. 9 - The flanged bolt coupling is fabricated by...Ch. 9 - Prob. 9.87RPCh. 9 - Compute Ix,Iy, and Ixy for the shaded region.Ch. 9 - Determine Ix and Ixy for the shaded region shown.Ch. 9 - Calculate Ix,Iy, and Ixy for the shaded region...Ch. 9 - For the shaded region shown, determine (a) Ix and...Ch. 9 - Use integration to find Ix,Iy, and Ixy for the...Ch. 9 - Determine the principal moments of inertia and the...Ch. 9 - The properties of the unequal angle section are...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 2.5 (B). A steel rod of cross-sectional area 600 mm² and a coaxial copper tube of cross-sectional area 1000 mm² are firmly attached at their ends to form a compound bar. Determine the stress in the steel and in the copper when the temperature of the bar is raised by 80°C and an axial tensile force of 60 kN is applied. For steel, E = 200 GN/m² with x = 11 x 10-6 per °C. E = 100 GN/m² with α = 16.5 × 10-6 For copper, per °C. [E.I.E.] [94.6, 3.3 MN/m².]arrow_forward3–16. A particle of mass m is embedded at a distance R from the center of a massless circular disk of radius R which can roll without slipping on the inside surface of a fixed circular cylinder of radius 3R. The disk is released with zero velocity from the position shown and rolls because of gravity, all motion taking place in the same vertical plane. Find: (a) the maximum velocity of the particle during the resulting motion; (b) the reaction force acting on the disk at the point of contact when it is at its lowest position. KAR 60° 3R M Fig. P3-16arrow_forwardI have figured out the support reactions, Ay = 240 kN, Ax = 0 kN, Ma = 639.2 kN*m and the constant term for V(x) is 240. I am not figuring out the function of x part right. Show how to derive V(x) and M(x) for this distributed load.arrow_forward
- 2.4 (A). A 75 mm diameter compound bar is constructed by shrinking a circular brass bush onto the outside of a 50 mm diameter solid steel rod. If the compound bar is then subjected to an axial compressive load of 160 kN determine the load carried by the steel rod and the brass bush and the compressive stress set up in each material. For steel, E 210 GN/m²; for brass, E = 100 GN/m². [I. Struct. E.] [100.3, 59.7 kN; 51.1, 24.3 MN/m².]arrow_forward1.7 (A). A bar ABCD consists of three sections: AB is 25 mm square and 50 mm long, BC is of 20 mm diameter and 40 mm long and CD is of 12 mm diameter and 50 mm long. Determine the stress set up in each section of the bar when it is subjected to an axial tensile load of 20 kN. What will be the total extension of the bar under this load? For the bar material, E = 210GN/m2. [32,63.7, 176.8 MN/mZ, 0.062mrn.l 10:41 مarrow_forward2.2 (A). If the maximum stress allowed in the copper of the cable of problem 2.1 is 60 MN/m2, determine the maximum tension which C3.75 kN.1 10:41 مarrow_forward
- 1.1 (A). A 25mm squarecross-section bar of length 300mm carries an axial compressive load of 50kN. Determine the stress set up ip the bar and its change of length when the load is applied. For the bar material E = 200 GN/m2. [80 MN/m2; 0.12mm.larrow_forward2.1 (A). A power transmission cable consists of ten copper wires each of 1.6 mm diameter surrounding three steel wires each of 3 mm diameter. Determine the combined E for the compound cable and hence determine the extension of a 30 m length of the cable when it is being laid with a tension of 2 kN. For steel, E200 GN/mZ; for copper, E = 100 GN/mZ. C151.3 GN/mZ; 9.6 mm.] 10:41 مarrow_forwardquestion 662 thank youarrow_forward
- 1.5 (A). A simple turnbuckle arrangement is constructed from a 40 mm outside diameter tube threaded internally at each end to take two rods of 25 mm outside diameter with threaded ends. What will be the nominal stresses set up in the tube and the rods, ignoring thread depth, when the turnbuckle cames an axial load of 30 kN? Assuming a sufficient strength of thread, what maximum load can be transmitted by the turnbuckle if the maximum stress is limited to 180 MN/mz? C39.2, 61.1 MN/m2, 88.4 kN.1arrow_forward1.3 (A). Define the terms shear stress and shear strain, illustrating your answer by means of a simple sketch. Two circular bars, one of brass and the other of steel, are to be loaded by a shear load of 30 kN. Determine the necessary diameter of the bars (a) in single shear, (b) in double shear, if the shear stress in the two materials must not exceed 50 MN/m2 and 100 MN/ mZ respectively. C27.6, 19.5, 19.5, 13.8mm.l 11arrow_forward1.4 (A). Two forkend pieces are to be joined together by a single steel pin of 25mm diameter and they are required to transmit 50 kN. Determine the minimum cross-sectional area of material required in one branch of either fork if the stress in the fork material is not to exceed 180 MN/m2. What will be the maximum shear stress in the pin? C1.39 x 10e4mZ; 50.9MN/mZ.] 10:41arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L

International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
moment of inertia; Author: NCERT OFFICIAL;https://www.youtube.com/watch?v=A4KhJYrt4-s;License: Standard YouTube License, CC-BY