Chapter 9, Problem 9.80RP

To determine

(a)

  $I_{x}and{I}_y$ for the shaded region.

Answer to Problem 9.80RP

  $I_x=56.2\times {10}^{6}m{m}^4$

  $I_y=33.8\times {10}^{6}m{m}^4$

Explanation of Solution

Given information:

The shaded region:

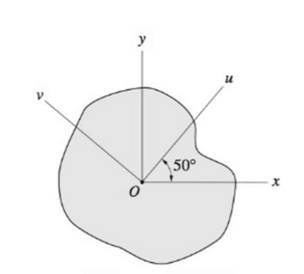
The principal moments of inertia at point O for the shaded region:

  $\begin{array}{l}{I}_1=60\times {10}^{6}m{m}^4\\ I_2=30\times {10}^{6}m{m}^4\end{array}$

The product of inertia with respect to the x- and y-axes is $I_{xy}=10\times {10}^{6}m{m}^4$.

Calculations:

  $\begin{array}{l}\text{Using equation 9}\text{.23:}\\ I_1=\frac{I_x+I_y}{2}+R\\ I_2=\frac{I_x+I_y}{2}-R\\ \text{solving the above two relations for }R\text{, we get:}\\ R=\frac{I_1-I_2}{2}=\frac{60-30}{2}\times {10}^6=15\times {10}^{6}m{m}^4\\ Also,fromtherelation:\left(I_x+I_y=I_1+I_2\right)\\ \therefore \frac{I_x+I_y}{2}=\frac{I_1+I_2}{2}=\frac{60+30}{2}\times {10}^6\\ \frac{I_x+I_y}{2}=45\times {10}^{6}m{m}^4\mathrm{...........}\left(a\right)\end{array}$

  $\begin{array}{l}and,fromequation9.22:\\ R^2={\left(\frac{I_x-I_y}{2}\right)}^2+I^2{}_{xy}\\ \therefore \frac{I_x-I_y}{2}=\sqrt{R^2-I^2{}_{xy}}={10}^6\sqrt{{15}^2-{10}^2}\\ \frac{I_x-I_y}{2}=11.18\times {10}^{6}m{m}^4\mathrm{..............}\left(b\right)\\ SolvingEqs.\left(a\right)and\left(b\right)\text{, }weget;\\ \Rightarrow I_x=56.2\times {10}^{6}m{m}^4\\ \Rightarrow I_y=33.8\times {10}^{6}m{m}^4\end{array}$

Conclusion:

For the shaded region shown, $I_x=56.2\times {10}^{6}m{m}^4$ and $I_y=33.8\times {10}^{6}m{m}^4$

To determine

(b)

  $I_{u}and{I}_v$ for the shaded region.

Answer to Problem 9.80RP

  $I_u=33.2\times {10}^{6}m{m}^4$

  $I_v=56.8\times {10}^{6}m{m}^4$

Explanation of Solution

Given information:

The shaded region:

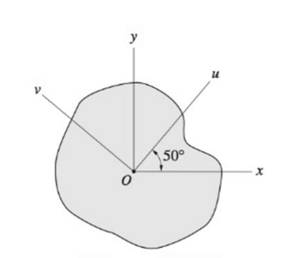
For the shaded region:

  $I_x=56.2\times {10}^{6}m{m}^4$

  $I_y=33.8\times {10}^{6}m{m}^4$

  $I_{xy}=10\times {10}^{6}m{m}^4$

Calculations:

  $\begin{array}{l}\text{Using the transformation equations 9}\text{.17 and 9}\text{.18;}\\ I_u=\frac{I_x+I_y}{2}+\frac{I_x-I_y}{2}\cos 2\theta -I_{xy}\sin 2\theta \\ =\left(45+11.18\cos {100}^o-10\sin {100}^o\right)\times {10}^6\\ \Rightarrow I_u=33.2\times {10}^{6}m{m}^4\\ I_v=\frac{I_x+I_y}{2}-\frac{I_x-I_y}{2}\cos 2\theta +I_{xy}\sin 2\theta \\ =\left(45-11.18\cos {100}^o+10\sin {100}^o\right)\times {10}^6\\ \Rightarrow I_v=56.8\times {10}^{6}m{m}^4\end{array}$

Conclusion:

For the shaded region, $I_u=33.2\times {10}^{6}m{m}^4$ and $I_v=56.8\times {10}^{6}m{m}^4$