
Concept explainers
(a)
The principal moments of inertia and the principal directions at the centroid C for the semicircular region.
Answer to Problem 9.51P
The principal moments of inertia:
Principal directions are along x and y axes
Explanation of Solution
Given information:
The semicircular region:
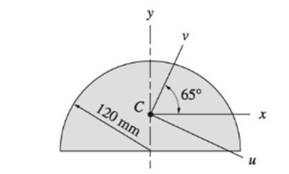
Calculations:
Because to symmetry, the x- and y- axes are the principal axes at C.
Hence,
Conclusion:
The principal moments of inertia at the centroid C for the semicircular region shown are
(b)
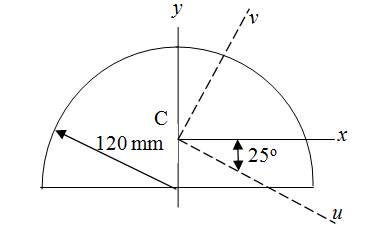
The moments and the products of inertia about the u-v-axes for the semicircular region shown.
Answer to Problem 9.51P
Moments of inertia:
Products of inertia:
Explanation of Solution
Given information:
For the semicircular region shown:
Calculations:
Conclusion:
For the semicircular region, the moments of inertia about the u-v axes are
Want to see more full solutions like this?
Chapter 9 Solutions
International Edition---engineering Mechanics: Statics, 4th Edition
- Consider a regenerative gas turbine power plant with two stages of compression and two stages of expansion. The compressor pressure ratio of the compressor is 3. Air enters each stage of compressor at 290 K and each stage of turbine at 1400 K. The regenerator has an effectiveness of 100%. Determine (a) The enthalpy at stage#2 in KJ/kg⭑ (b) The enthalpy at stage#6 in KJ/kg* (c) The enthalpy at stage#9 in KJ/kg (d) The enthalpy at stage#10 in KJ/kg (e)The mass flow rate of air needed to develop a net power output of 50 MW* *For all final answers please enter the integer part only, (ie 1234) and do not include the decimal part and the decimal point No rounding in your calculation. Compressor stage 1 Regenerator www HX ww 9 Combustor Reheat Intercooler ww Compressor stage 2 Turbine 1 combustor Turbine 2arrow_forwardDesign a proportional derivitivecontroller for a plant orsystemthat satisfies the following specifications : 1. is steady-state error is less than 2 % for a ramp input. 2.) Damping ratio (zeta) is greater than 0.7have determined the 3. Once youvalue of kp and kd, then plotthe response of the compensated(with controller) and uncompensated( without the controller, only the plantsystem using MATLAB.arrow_forwardExample 2 The particle has a mass of 0.5 kg and is confined to move along the smooth horizontal slot due to the rotation of the arm OA. Determine the force of the rod on the particle and the normal force of the slot on the particle when 0 = 30°. The rod is rotating with a constant angular velocity 2 rad/s. Assume the particle contacts only one side of the slot at any instant. B =2 rad/s 0.5 m 0.5(9.81)N r F 30° Narrow_forward
- A gas turbine cycle has two stages of compression, with an intercooler between the stages. Air enters the first stage at 100 kPa, 300 K. The pressure efficiency of 82%. Air exits the intercooler at 330 K. Calculate the temperature at the exit of each compressor stage and the total specific work required.arrow_forwardFor problem 13, your answer should be the same as problem 12. Calculate the flow velocity and the heat transfer/area of the outer surfaces for both duct geometries to see the performance difference of the two designs.arrow_forwardOne end of a thin uniform rod of mass m and length 31 rests against a smooth vertical wall. The other end of the rod is attached by a string of length 1 to a fixed point O which is located a distance 21 from the wall. A horizontal force of magnitude F₁ is applied to the lower end of the rod as shown. Assuming the rod and the string remain in the same vertical plane perpendicular to the wall, find the angle 0 between the rod and the wall at the position of static equilibrium. Notes: This quiz is going to walk you through a sequence of steps to do this. It won't give you the answers, but it will hopefully get you to see how to approach problems like this so that you have a working reference/template in the future. This is actually a modified version of a problem from the textbook (6.3). Note that in that problem, is not actually given. It has been introduced for convenience as we move through solving the problem, and should not show up in the final answer. DO NOT DO PROBLEM 6.3. It is…arrow_forward
- varrow_forward13.64 The shaft shown in Sketch h transfers power between the two pulleys. The tension on the slack side (right pul- ley) is 30% of that on the tight side. The shaft rotates at 900 rpm and is supported uniformly by a radial ball bearing at points 0 and B. Select a pair of radial ball bear- ings with 99% reliability and 40,000 hr of life. Assume Eq. (13.83) can be used to account for lubricant clean- liness. All length dimensions are in millimeters. Ans. Cmin = 42,400 N.arrow_forwardA 4 inch wide, 12 inch tall cross section beam is subjected to an internal shear of 5.5 kips. What is the maximum transverse shear stress in the beam in psi if this bending is about the x axis?arrow_forward
- A Brayton cycle produces 14 MW with an inlet state of 17°C, 100 kPa, and a compression ratio of 16:1. The heat added in the combustion is 960 kJ/kg. 0.7 MW of heat transferred from the turbine to the environment. What are the highest temperature and the mass flow rate of air? Assume cold air properties.arrow_forward. A gas turbine with air enters the compressor at 300 K, 1 bar, and exits from the turbine at 750 K, 1 bar. The thermal efficiency of the cycle is 40.1% and the back work ratio (BWR) is 0.4. Find the pressure ratio of the cycle. Assume variable specific heat.arrow_forwardA regenerative gas turbine power plant is shown in Fig. below. Air enters the compressor at 1 bar, 27°C with a mass flow rate of 0.562 kg/s and is compressed to 4 bar. The isentropic efficiency of the compressor is 80%, and the regenerator effectiveness is 90%. All the power developed by the high-pressure turbine is used to run the compressor. The low-pressure turbine provides the net power output. Each turbine has an isentropic efficiency of 87% and the temperature at the inlet to the highpressure turbine is 1200 K. Assume cold air properties, determine: a. The net power output, in kW. b. The thermal efficiency of the cycle.arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
