
Find the moment and product of inertia of the area with respect to x and y axes about through
Answer to Problem 9.192RP
The moment of inertia of the area with respect to x about through
The moment of inertia of the area with respect to y about through
The product of inertia of the area with respect to x and y axes about through
Explanation of Solution
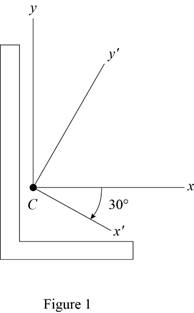
Sketch the cross section as shown in Figure 1.
Refer to Figure 9.13.
The moment of inertia
The moment of inertia
Refer to Problem 9.191.
Sketch the cross section as shown in Figure 2.
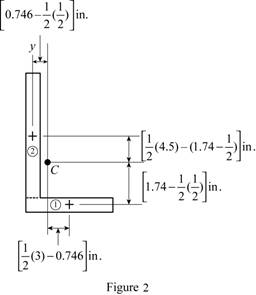
Express the product of inertia as shown below:
Here,
Applying parallel axis theorem,
When the x and y axis is symmetry.
Refer to Figure 1.
Find the area of semicircle section 1 as shown below:
Here,
Substitute
Find the area of rectangle section 2 as shown below:
Here,
Substitute
Find the centroid for section 1 about x axis
Find the centroid for section 1 about x axis
Find the centroid for section 1 about y axis
Find the centroid for section 2 about x axis
Find the product of inertia of the area with respect to x and y axes by using parallel axis theorem as shown below:
Substitute
The Mohr circle is defined by the diameter XY, where
Find the average moment of inertia
Here,
Substitute
Find the radius (R) using the relation as shown below:
Here, R is radius and
Substitute
Sketch the Mohr circle as shown in Figure 3.

Refer to Figure 2.
Substitute
Find the angle
Find the moment of inertia of the area with respect to x about through
Here,
Substitute
Thus, the moment of inertia of the area with respect to x about through
Find the moment of inertia of the area with respect to y about through
Substitute
Thus, the moment of inertia of the area with respect to y about through
Find the product of inertia of the area with respect to y about through
Substitute
Thus, the product of inertia of the area with respect to x and y axes about through
(b)
Find the orientation of the principal axes through the centroid and corresponding values.
(b)
Answer to Problem 9.192RP
The orientation of the principal axes at the origin is
The maximum moment of inertia is
The minimum moment of inertia is
Explanation of Solution
Calculation:
Find the orientation of the principal axes through at origin as shown below.
Refer part a.
Thus, the orientation of the principal axes at the origin is
Sketch the orientation axis as shown in Figure 4.
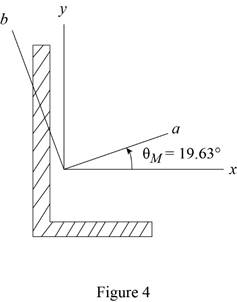
Find the maximum moment
Substitute
Thus, the maximum moment of inertia is
Find the minimum moment
Substitute
Thus, the minimum moment of inertia is
Want to see more full solutions like this?
Chapter 9 Solutions
Connect 1 Semester Access Card for Vector Mechanics for Engineers: Statics and Dynamics
- Consider 0.65 kg of N2 at 300 K, 1 bar contained in a rigid tank connected by a valve to another rigid tank holding 0.3 kg of CO2 at 300 K, 1 bar. The valve is opened and gases are allowed to mix, achieving an equilibrium state at 290 K. Determine: (a) the volume of each tank, in m³. (b) the final pressure, in bar. (c) the magnitude of the heat transfer to or from the gases during the process, in kJ. (d) the entropy change of each gas and of the overall system, in kJ/K.arrow_forwardBài 1. Cho cơ hệ như hình 1. Hình biểu diễn lược đổ cơ hệ tại vị trí cân bằng tĩnh. Trục tọa độ Oy hướng theo phương chuyển động của vật 1, gốc O đặt tại vị trí cân bằng của vật 1(tức khi lò xo biến dạng tĩnh). Bỏ qua khối lượng của thanh số 3. Vật rắn 2 là pulley 2 tầng đồng chất có bán kính ngoài 21, bán kính trong I, bán kính quán tính đối với trục qua tâm P-1.5, khối lượng m:. Vật rắn 4 là thanh thắng đồng chất có khối lượng m, chiều dài 1. Cho các số liệu: m = 2kg, m= = 5kg, m = 4kg, k=40(N/cm), ! – 0.8(m),r=0.1(m). Điều kiện đầu y; =0.5 cm );j = 10 cm/s) . Giả sử hệ dao động bé, Vật rắn 2 chuyển động lăn không trượt trên mặt phẳng ngang. 1. Viết phương trình chuyển động của hệ. 2. Xác định tần số dao động tự do của hệ. 3. Xác định đáp ứng dao động tự do của hệ. dây dây 1 2r Hình 1 y 3 -2 I k www. -2arrow_forwardHints: Find the closed loop transfer function and then plot the step response for diFerentvalues of K in MATLAB. Show step response plot for different values of K. Auto Controls Show solutions and provide matlab code NO COPIED ANSWERS OR WILL REPORTarrow_forward
- Obtain the response of the system shown below for a parabolic or acceleration input r(t);where Auto Controls Show full solutionarrow_forwardProblem Statement A large plate of insulating material 8 cm thick has in it a 3 cm-diam hole, with axis normal to the surface. The temperature of the surroundings are 1800 K at one side of the plate and 400 K on the other side. Insulating plate D= 3 cm H= 8 cm Considering the sides of the hole to be black, (a) Draw a system of resistors that can be used to solve for the various heat transfer rates. For full credit you must label all "voltages", "currents," and resistances present. (b) Estimate the radiative heat transfer through the hole.arrow_forwardUsing MATLAB, plot the unit-step response curve for the following transfer function and Using MATLAB, obtain the rise time, peak time, maximum overshoot, and settling time. Auto Controls Provide codesarrow_forward
- Use Routh's stability criterion to determine how many roots with positive real partsthe following equations have Auto Controls Show full solutionsarrow_forwardPlot the unit step and unit ramp response curve for the following closed loop transferfunction using MATLAB. Indicate clearly the input and output in your plot Auto Controls provide matlab codearrow_forwardUsing a "for loop" in MATLAB program to obtain the unit-step response of thissystem for the following four cases in a single plot What can you observe from the plot? Auto Controls Provide matlab codearrow_forward
- Problem 2 (40 Points) A particle of mass m is embedded at a distance a from the center of a massless circular disk of radius r. The disk rolls without slipping down a plane inclined at an angle a with the horizontal. A horizontal force of Ễ = −Fxî + Fyĵ resists motion of the disk down the plane by pushing on the disk at the axle that runs through the center of the disk. a) Find the kinetic energy T. (10 points) b) Find the potential energy V. (10 points) c) Write a position vector to the axle at the center of the wheel in terms of x and y. (10 points) d) Using virtual work, find the applied force Q₁ that would go in Lagrange's Equations. DO NOT WRITE OUT OR SOLVE LAGRANGES'S EQUATIONS. (10 points) x r m e 10 g F α HINTS 1) Consider using the STATIONARY red xy frame a reference frame from which to draw vectors 2) The red xy system DOES NOT move. It is stationary. 3) Consider that the disk rolls a distance of re down the ramparrow_forwardDraw a counter balance circuit of a vertical cylinder. using counter balance valve and external load.arrow_forwardplease sketch a stress-strain diagram for a typical structural steel in tension and display all of the important features.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





