College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 9, Problem 84AP
A Hydrometer is an instrument used to determine liquid density. A simple one is sketched in Figure P9.84. The bulb of a syringe is squeezed and released to lift a sample of the liquid of interest into a tube containing a calibrated rod of known density. (Assume the rod is cylindrical.) The rod. of length L and average density ρ0, floats partially immersed in the liquid of density ρ. A length h of the rod protrudes above the surface of the liquid. Show that the density of the liquid is given by
Figure P9.84
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A planar double pendulum consists of two point masses \[m_1 = 1.00~\mathrm{kg}, \qquad m_2 = 1.00~\mathrm{kg}\]connected by massless, rigid rods of lengths \[L_1 = 1.00~\mathrm{m}, \qquad L_2 = 1.20~\mathrm{m}.\]The upper rod is hinged to a fixed pivot; gravity acts vertically downward with\[g = 9.81~\mathrm{m\,s^{-2}}.\]Define the generalized coordinates \(\theta_1,\theta_2\) as the angles each rod makes with thedownward vertical (positive anticlockwise, measured in radians unless stated otherwise).At \(t=0\) the system is released from rest with \[\theta_1(0)=120^{\circ}, \qquad\theta_2(0)=-10^{\circ}, \qquad\dot{\theta}_1(0)=\dot{\theta}_2(0)=0 .\]Using the exact nonlinear equations of motion (no small-angle or planar-pendulumapproximations) and assuming the rods never stretch or slip, determine the angle\(\theta_2\) at the instant\[t = 10.0~\mathrm{s}.\]Give the result in degrees, in the interval \((-180^{\circ},180^{\circ}]\).
What are the expected readings of the ammeter and voltmeter for the circuit in the figure below? (R = 5.60 Ω, ΔV = 6.30 V)
ammeter
I =
simple diagram to illustrate the setup for each law- coulombs law and biot savart law
Chapter 9 Solutions
College Physics
Ch. 9.2 - Suppose you have one cubic meter of gold, two...Ch. 9.3 - The pressure at the bottom of a glass filled with...Ch. 9.4 - Several common barometers are built using a...Ch. 9.4 - Blood pressure is normally measured with the cuff...Ch. 9.5 - Atmospheric pressure varies from day to day. The...Ch. 9.5 - The density of lead is greater than iron, and both...Ch. 9.6 - You observe two helium balloons floating next to...Ch. 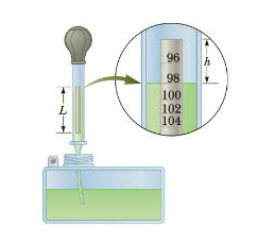9 - The three containers in Figure CQ9.1 are filled...Ch. 9 - The density of air is 1.3 kg/m3 at sea level. From...Ch. 9 - Four solid, uniform objects are placed in a...
Ch. 9 - Figure CQ9.4 shows aerial views from directly...Ch. 9 - Prob. 5CQCh. 9 - Prob. 6CQCh. 9 - Water flows along a streamline down a river of...Ch. 9 - During inhalation, the pressure in the lungs is...Ch. 9 - The water supply for a city is often provided from...Ch. 9 - An ice cube is placed in a glass of water. What...Ch. 9 - Prob. 11CQCh. 9 - Will an ice cube float higher in water or in an...Ch. 9 - Prob. 13CQCh. 9 - Prob. 14CQCh. 9 - A person in a boat floating in a small pond throws...Ch. 9 - One of the predicted problems due to global...Ch. 9 - An 81.5kg man stands on a horizontal surface. (a)...Ch. 9 - The weight of Earths atmosphere exerts an average...Ch. 9 - Calculate the mass of a solid gold rectangular bar...Ch. 9 - Prob. 5PCh. 9 - Prob. 6PCh. 9 - Suppose a distant world with surface gravity of...Ch. 9 - Prob. 8PCh. 9 - (a) Calculate the absolute pressure at the bottom...Ch. 9 - Mercury is poured into a U-tube as shown in Figure...Ch. 9 - A collapsible plastic bag (Fig. F9.11) contains a...Ch. 9 - A hydraulic jack has an input piston of area 0.050...Ch. 9 - A container is filled to a depth of 20.0 cm with...Ch. 9 - Blaise Pascal duplicated Torricellis barometer...Ch. 9 - A sphygmomanometer is a device used to measure...Ch. 9 - Piston in Figure P9.16 has a diameter of 0.25...Ch. 9 - Buoyant Forces and Archimedes Principle A...Ch. 9 - Prob. 18PCh. 9 - A small ferryboat is 4.00 m wide and 6.00 m long....Ch. 9 - A 62.0-kg survivor of a cruise line disaster rests...Ch. 9 - A hot-air balloon consists of a basket banging...Ch. 9 - A large balloon of mass 226 kg is filled with...Ch. 9 - A spherical weather balloon is filled with...Ch. 9 - The average human has a density of 945 kg/m3 after...Ch. 9 - On October 21, 2001, Ian Ashpole of the United...Ch. 9 - The gravitational force exerted on a solid object...Ch. 9 - A cube of wood having an edge dimension of 20.0 cm...Ch. 9 - A light spring of force constant k = 160 N/m rests...Ch. 9 - A sample of an unknown material appears to weigh...Ch. 9 - An object weighing 300 N in air is immersed in...Ch. 9 - A 1.00-kg beaker containing 2.00 kg of oil...Ch. 9 - A horizontal pipe narrows from a radius of 0.250 m...Ch. 9 - A large water tank is 3.00 m high and filled lo...Ch. 9 - Wafer flowing through a garden hose of diameter...Ch. 9 - Prob. 35PCh. 9 - Prob. 36PCh. 9 - A hypodermic syringe contain a medicine with the...Ch. 9 - When a person inhales, air moves down the bronchus...Ch. 9 - A jet airplane in level flight has a mass of 8.66 ...Ch. 9 - A man attaches a divider to an outdoor faucet so...Ch. 9 - Prob. 41PCh. 9 - Prob. 42PCh. 9 - A jet of water squirts out horizontally from a...Ch. 9 - A large storage tank, open to the atmosphere at...Ch. 9 - The inside diameters of the larger portions of the...Ch. 9 - Water is pumped through a pipe of diameter 15.0 cm...Ch. 9 - Old Faithful geyser in Yellowstone Park erupts at...Ch. 9 - The Venturi tube shown in Figure P9.48 may be used...Ch. 9 - Prob. 49PCh. 9 - Prob. 50PCh. 9 - A certain fluid has a density of 1.080 kg/m3 and...Ch. 9 - Whole blood has a surface tension of 0.058 N/m and...Ch. 9 - Prob. 53PCh. 9 - Prob. 54PCh. 9 - Prob. 55PCh. 9 - Prob. 56PCh. 9 - Spherical panicles of a protein of density 1.8...Ch. 9 - A hypodermic needle is 3.0 era in length and 0.30...Ch. 9 - Prob. 59PCh. 9 - The aorta in humans has a diameter of about 2.0...Ch. 9 - Prob. 61PCh. 9 - Glycerin in water diffuses along a horizontal...Ch. 9 - Prob. 63PCh. 9 - Small spheres of diameter 1.00 mm fall through 20C...Ch. 9 - The Deformation of Solids 65. A 200.-kg load is...Ch. 9 - A 25.0-m long steel cable with a cross-sectional...Ch. 9 - A plank 2.00 cm thick and 15.0 cm wide is firmly...Ch. 9 - Artificial diamonds can be made using...Ch. 9 - For safety in climbing, a mountaineer uses a nylon...Ch. 9 - Assume that if the shear stress in steel exceeds...Ch. 9 - Bone has a Youngs modulus of 18 109 Pa. Under...Ch. 9 - A stainless-steel orthodontic: wire is applied to...Ch. 9 - A high-speed lifting mechanism supports an 800.-kg...Ch. 9 - The deepest point in the ocean is in the Mariana...Ch. 9 - Prob. 75PCh. 9 - The total cross-sectional area of the load-bearing...Ch. 9 - An iron block of volume 0.20 m5 is suspended from...Ch. 9 - Prob. 78APCh. 9 - In most species of clingfish (family...Ch. 9 - Prob. 80APCh. 9 - Prob. 81APCh. 9 - Superman attempts to drink water through a very...Ch. 9 - The human brain and spinal cord are immersed in...Ch. 9 - A Hydrometer is an instrument used to determine...Ch. 9 - Prob. 85APCh. 9 - A helium-filled balloon, whose envelope has a mass...Ch. 9 - A light spring of constant A = 90.0 N/m is...Ch. 9 - A U-tube open at both ends is partially filled...Ch. 9 - In about 1657. Otto von Guericke, inventor of the...Ch. 9 - Oil having a density of 930 kg/m3 floats on water....Ch. 9 - Prob. 91AP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A circular coil with 100 turns and a radius of 0.05 m is placed in a magnetic field that changes at auniform rate from 0.2 T to 0.8 T in 0.1 seconds. The plane of the coil is perpendicular to the field.• Calculate the induced electric field in the coil.• Calculate the current density in the coil given its conductivity σ.arrow_forwardAn L-C circuit has an inductance of 0.410 H and a capacitance of 0.250 nF . During the current oscillations, the maximum current in the inductor is 1.80 A . What is the maximum energy Emax stored in the capacitor at any time during the current oscillations? How many times per second does the capacitor contain the amount of energy found in part A? Please show all steps.arrow_forwardA long, straight wire carries a current of 10 A along what we’ll define to the be x-axis. A square loopin the x-y plane with side length 0.1 m is placed near the wire such that its closest side is parallel tothe wire and 0.05 m away.• Calculate the magnetic flux through the loop using Ampere’s law.arrow_forward
- Describe the motion of a charged particle entering a uniform magnetic field at an angle to the fieldlines. Include a diagram showing the velocity vector, magnetic field lines, and the path of the particle.arrow_forwardDiscuss the differences between the Biot-Savart law and Coulomb’s law in terms of their applicationsand the physical quantities they describe.arrow_forwardExplain why Ampere’s law can be used to find the magnetic field inside a solenoid but not outside.arrow_forward
- 3. An Atwood machine consists of two masses, mA and m B, which are connected by an inelastic cord of negligible mass that passes over a pulley. If the pulley has radius RO and moment of inertia I about its axle, determine the acceleration of the masses mA and m B, and compare to the situation where the moment of inertia of the pulley is ignored. Ignore friction at the axle O. Use angular momentum and torque in this solutionarrow_forwardA 0.850-m-long metal bar is pulled to the right at a steady 5.0 m/s perpendicular to a uniform, 0.650-T magnetic field. The bar rides on parallel metal rails connected through a 25-Ω, resistor (Figure 1), so the apparatus makes a complete circuit. Ignore the resistance of the bar and the rails. Please explain how to find the direction of the induced current.arrow_forwardFor each of the actions depicted, determine the direction (right, left, or zero) of the current induced to flow through the resistor in the circuit containing the secondary coil. The coils are wrapped around a plastic core. Immediately after the switch is closed, as shown in the figure, (Figure 1) in which direction does the current flow through the resistor? If the switch is then opened, as shown in the figure, in which direction does the current flow through the resistor? I have the answers to the question, but would like to understand the logic behind the answers. Please show steps.arrow_forward
- When violet light of wavelength 415 nm falls on a single slit, it creates a central diffraction peak that is 8.60 cm wide on a screen that is 2.80 m away. Part A How wide is the slit? ΟΙ ΑΣΦ ? D= 2.7.10-8 Submit Previous Answers Request Answer × Incorrect; Try Again; 8 attempts remaining marrow_forwardTwo complex values are z1=8 + 8i, z2=15 + 7 i. z1∗ and z2∗ are the complex conjugate values. Any complex value can be expessed in the form of a+bi=reiθ. Find θ for (z1-z∗2)/z1+z2∗. Find r and θ for (z1−z2∗)z1z2∗ Please show all stepsarrow_forwardCalculate the center of mass of the hollow cone shown below. Clearly specify the origin and the coordinate system you are using. Z r Y h Xarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
Fluids in Motion: Crash Course Physics #15; Author: Crash Course;https://www.youtube.com/watch?v=fJefjG3xhW0;License: Standard YouTube License, CC-BY