
Concept explainers
Use a table of values to graph each equation.
Answer to Problem 5QC
The domain is all real numbers. The range is all real numbers.
Explanation of Solution
Given:
The equation:
Concept Used:
A line is a straight one-dimensional figure having no thickness and extending infinitely in both directions. A line is sometimes called a straight line or, more archaically, a right line, to emphasize that it has no "wiggles" anywhere along its length.
The domain of a function is the complete set of possible values of the independent variable. The domain is the set of all possible x-values which will make the function "work", and will output real y-values.
The range of a function is the complete set of all possible resulting values of the dependent variable ( y, usually), after we have substituted the domain.
Calculation:
Rewrite the equation in slope and intercept form:
The equation:
Make table to get some points on the graph
| x | (x, y) | |
| 0 | (0, − 4) | |
| − 3 | ( − 3 ,− 8 ) | |
| −6 | (− 6 , − 12 ) | |
| 3 | (3, 0) | |
| 6 | (6, 4) |
Graph the ordered pairs, and connect them to create a smooth straight line. The straight line is having x and y intercept at x = 3 and y = − 4. Extended both sides to infinity
| Slope − intercept form of a straight line is y = mx + b
Where m is the slope of the line and b is the y − intercept. The graph is a straight line with a slope The domain is all real numbers. The range is all real numbers. | 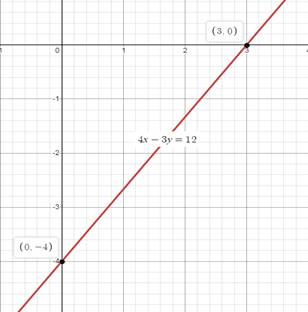 |
Chapter 9 Solutions
Algebra 1
Additional Math Textbook Solutions
Pre-Algebra Student Edition
Basic Business Statistics, Student Value Edition
A First Course in Probability (10th Edition)
College Algebra with Modeling & Visualization (5th Edition)
Algebra and Trigonometry (6th Edition)
- > > > we are hiring Salesforce Admin Location: Remote Key Responsibilities: Administer Salesforce Sales & Revenue Cloud (CPQ & Billing) Configure workflows, validation rules & dashboards Automate processes using Flows & Process Builder Collaborate with Sales, Finance & Marketing teams Manage user roles & security Apply: Hr@forcecraver.comarrow_forwardAnswer this questionarrow_forward1. vector projection. Assume, ER1001 and you know the following: ||||=4, 7=-0.5.7. For each of the following, explicitly compute the value. འབ (a) (b) (c) (d) answer. Explicitly compute ||y7||. Explain your answer. Explicitly compute the cosine similarity of and y. Explain your Explicitly compute (x, y). Explain your answer. Find the projection of onto y and the projection of onto .arrow_forward
- 2. Answer the following questions using vectors u and v. --0-0-0 = find the the cosine similarity and the angle between u and v. འརྒྱ (a) (b) find the scalar projection of u onto v. (c) find the projection of u onto v. (d) (e) (f) find the scalar projection of onto u. find the projection of u onto u. find the projection of u onto and the projection of onto . (Hint: find the inner product and verify the orthogonality)arrow_forwardPlease type out answerarrow_forwardPlease type out answerarrow_forward
- Please type out answerarrow_forwardUsing f(x) = log x, what is the x-intercept of g(x) = log (x + 4)? Explain your reasoning. Please type out answerarrow_forwardThe function f(x) = log x is transformed to produce g(x) = log (x) – 3. Identify the type of transformation and describe the change. Please type out answerarrow_forward
- Each graph below is the graph of a system of three linear equations in three unknowns of the form Ax = b. Determine whether each system has a solution and, if it does, the number of free variables. A. O free variables ✓ B. no solution C. no solution D. no solution E. 1 free variable F. 1 free variablearrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5 Please type out answerarrow_forwardSolve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1 Please type out answerarrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





