
Concept explainers
To Graph:
The given function.
Explanation of Solution
Given Information:
Given equation is :
y=−3x2+6x−4
Concept Used :
- Quadratic Functions:
- Quadratic functions are non-linear and are of the form:
f(x)=ax2+bx+c;a≠0
This is the standard form of Quadratic function.
- Shape of the graph of a Quadratic function is called Parabola.
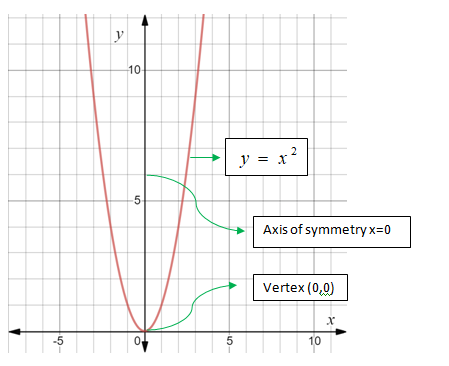
- Parabolas are symmetric about a central line called Axis Of Symmetry.
- The axis of symmetry intersects a parabola only at one point , called the Vertex.
- Parent Function:
y=x2
- Standard Form :
f(x)=ax2+bx+c;a≠0
- Type of Graph:
Parabola
- Axis of Symmetry: Passes through the vertex and divides the parabola into two congruent halves.
x=−b2a
- y-intercept = The y coordinate of the point at which the graph intersects y-axis = c
- Graph:
- If a > 0 ,
- The graph of ax2+bx+c opens upward.
- The lowest point on the graph is the minimum.
- If a < 0 ,
- The graph of ax2+bx+c opens downward.
- The highest point on the graph is the maximum.
- The maximum or the minimum is the vertex.
Calculation:
- In the equation y=−3x2+6x−4 ; comparing it with standard form of quadratic equation , we have a = -3 , b = 6 , c = -4 .
- Find equation of Axis of Symmetry :
y=ax2+bx+c...........................[standard_form]x=−b2a.....................................[formula_of_axis_of_symmetry]x=−62(−3)=1..........................[a=−3,b=6]
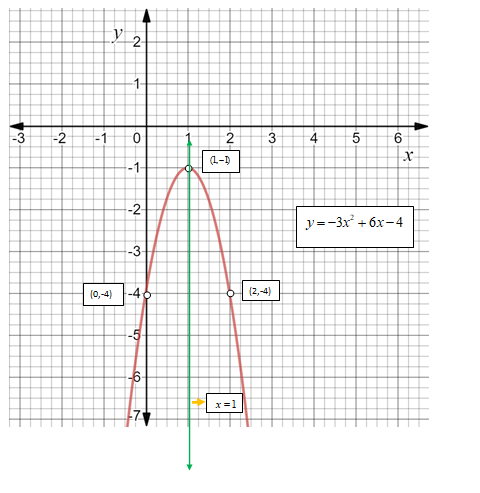
The equation of axis of symmetry is x=1
- Find the Vertex and determine whether it is maximum or minimum:
Since axis of symmetry passes through the vertex , we have x coordinate of the vertex (x,y) is x=1
Substituting the value of x=1in the equation y=−3x2+6x−4
y=−3x2+6x−4y=−3(1)2+6(1)−4...............[x=1]y=−3+6−4..................................[simplify]y=−1
The vertex is at (1,−1) .
Since the a = -3 < 0 .So, the graph opens downward .Hence, the vertex is the maximum.
- Find y-intercept :
The y-coordinate of the point at which the graph cuts the y-axis is the y-intercept.
y-intercept always occurs at (0,c) and c = -4 here.
So, y-intercept = -4 and is located at (0,-4).
- The axis of symmetry cuts the parabola into two equal parts . So, if there is a point on one side, there is a corresponding point on the other side that is at a same distance from the axis of symmetry and the same y-value.
| x | y |
| -1 | -13 |
| 0 | -4 |
| 1 | -1 |
| 2 | -4 |
| 3 | -13 |
- Connect the points with a smooth curve.
Graph :
Chapter 9 Solutions
Algebra 1
Additional Math Textbook Solutions
Thinking Mathematically (6th Edition)
Basic Business Statistics, Student Value Edition
Intro Stats, Books a la Carte Edition (5th Edition)
Elementary Statistics (13th Edition)
A First Course in Probability (10th Edition)
- Please use the infinite series formula and specify how you did each step. Thank you.arrow_forward8) Solve the given system using the Gaussian Elimination process. 2x8y = 3 (-6x+24y = −6arrow_forward7) Solve the given system using the Gaussian Elimination process. (5x-4y = 34 (2x - 2y = 14arrow_forward
- 33 (a) (b) Let A(t) = = et 0 0 0 cos(t) sin(t) 0-sin(t) cos(t)) For any fixed tЄR, find det(A(t)). Show that the matrix A(t) is invertible for any tЄ R, and find the inverse (A(t))¹.arrow_forwardUse the infinite geometric sum to convert .258 (the 58 is recurring, so there is a bar over it) to a ratio of two integers. Please go over the full problem, specifying how you found r. Thank you.arrow_forwardH.w: Find the Eigen vectors for the largest Eigen value of the system X1+ +2x3=0 3x1-2x2+x3=0 4x1+ +3x3=0arrow_forward
- need help with 5 and 6 pleasearrow_forward1) Given matrix A below, answer the following questions: a) What is the order of the matrix? b) What is the element a13? c) What is the element a₁₁? 4 -1arrow_forward[25 points] Given the vector let v = ER² and the collection of vectors ε = E-{)·()}-{☹) (9)} = {(A)·(9)}· B: = and C = · {(6)·(})}· answer the following question. (a) (b) (c) (d) (e) verify Verify is a basis for R² and find the coordinate [] of under ε. Verify B is a basis for R2 and find the coordinate []B of ʊ Verify C is a basis for R2 and find the coordinate []c of under ε. under ε. Find the change-of-basis matrix [I]+B from basis B to basis ε, and EE+BUB Find the change-of-basis matrix [I]B+ε from basis Ɛ to basis B, and verify [U]B= [] B+EVEarrow_forward
- Explain the following terms | (a) linear span (b) dimension of vector space (c) linearly independent (d) linearly dependent (e) rank of matrix Aarrow_forward3. Let u = 3/5 √ = and = -4/5 -() Define V span{ū, }. (a) (b) (c) Show that {u, } is orthonormal and forms a basis for V. Explicitly compute Projy w. Explicitly give a non-zero vector in V+.arrow_forwardIs 1.1 0.65 -3.4 0.23 0.4 -0.44 a basis for R3? You must explain your answer 0arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





