Chapter 9, Problem 36AP

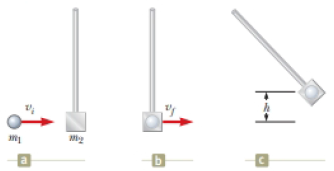
(a) Figure P9.36 shows three points in the operation of the ballistic pendulum discussed in Example 9.6 (and shown in Fig. 9.10b). The projectile approaches the pendulum in Figure P9.36a. Figure P9.36b shows the situation just after the projectile is captured in the pendulum. In Figure P9.36c, the pendulum arm has swung upward and come to rest momentarily at a height A above its initial position. Prove that the ratio of the kinetic energy of the projectile–pendulum system immediately after the collision to the kinetic energy immediately before is m_1|/(m₁ + m₂). (b) What is the ratio of the momentum of the system immediately after the collision to the momentum immediately before? (c) A student believes that such a large decrease in mechanical energy must be accompanied by at least a small decrease in momentum. How would you convince this student of the truth?

Figure P9.36 Problem. 36 and 43. (a) A metal ball moves toward the pendulum. (b) The ball is captured by the pendulum. (c) The ball–pendulum combination swings up through a height h before coming to rest.