Chapter 9, Problem 1P

(a) Using the superposition theorem, determine the current through the 12 $\Omega$ resistor of Fig. 9.125.

b. Convert both voltage sources to current sources and recalculate the current to the 12 $\Omega$ resistor.

c. How do the results of parts (a) and (b) compare?

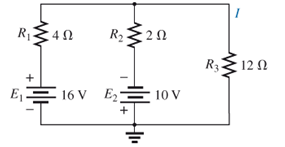
Fig. 9.125

To determine

(a)

The current through $\text{12Ω}$ resistor using superposition theorem for the given network.

Answer to Problem 1P

The current through $\text{12Ω}$ resistor using superposition theorem for the given network is $\text{0}\text{.1A in upward direction}$.

Explanation of Solution

Given:

The resistors values are ${\text{R}}_1{\text{=4Ω,R}}_2{\text{=2Ω and R}}_3\text{=12Ω}$.

The voltage sources are ${\text{E}}_{\text{1}}{\text{=16V and E}}_{\text{2}}\text{=-10V}$.

Concept Used:

Elements in the series have the same current.

Elements in the parallels have the same voltage.

Superposition theorem states that in any linear bilateral network having more than one source response in any one of the branches is equal to algebraic sum of the responses caused by individual source while rest of the sources are replaced by their internal impedances.

Short circuit the voltage source and open circuit the current source.

If the resistors are in series, then the value of the equivalent resistance for N series resistors is

${\text{R}}_{\text{eq}}{\text{=R}}_{\text{1}}{\text{+R}}_{\text{2}}\text{+}\mathrm{.........}{\text{+R}}_{\text{N}}$.

If the resistors are in parallel, then the value of the equivalent resistance for N series resistors is

$\frac{1}{{\text{R}}_{\text{eq}}}=\frac{1}{{\text{R}}_{\text{1}}}+\frac{1}{{\text{R}}_{\text{2}}}+\mathrm{.........}\text{+}\frac{1}{{\text{R}}_{\text{N}}}$.

The special case for only two parallel resistors is

${\text{R}}_{\text{eq}}\text{=}\frac{{\text{R}}_1{\text{R}}_2}{{\text{R}}_1+{\text{R}}_2}$.

Current: $\text{I=}\frac{\text{V}}{\text{R}}$

$\begin{array}{l}\text{Where V is the voltage}\text{.}\\ \text{ R is the resistance}\text{.}\end{array}$.

Current division is used to express the current across one of several parallel resistors in terms of current across the combination:

If there are two resistors in parallel then the current across second resistor is

$\begin{array}{l}{\text{I}}_{\text{2}}\text{=I(}\frac{{\text{R}}_{\text{1}}}{{\text{R}}_{\text{1}}{\text{+R}}_{\text{2}}}\text{)}\\ \text{Where I is the source current}\text{.}\\ {\text{ I}}_{\text{2}}{\text{ is the current across resistor R}}_{\text{2}}\text{.}\end{array}$

Calculation:

Firstly, short circuit the voltage source

$\begin{array}{l}\text{Total resitance}\\ R_T=R_1+R_2\left|\right|R_3=4+2\left|\right|12\\ R_T=\frac{12(2)}{12+2}+4\\ R_T=5.71\Omega \\ \\ \text{Total current=}\frac{16}{5.71}=2.8A\\ \text{Using current division rule,}\\ {\text{Current through R}}_{\text{3}}\text{ resistor is}\\ 2.8\frac{2}{2+12}=0.4A\text{ in downward direction }\mathrm{....}\text{(1)}\\ \\ \\ {\text{Secondly,short circuit the E}}_{\text{1}}\text{ voltage source}\text{.}\\ \text{Total resitance}\\ R_T=R_1\left|\right|R_3+R_2=4\left|\right|12+2\\ R_T=\frac{12(4)}{12+4}+2\\ R_T=5\Omega \\ \\ \text{Total current=}\frac{10}{5}=2A\\ \text{Using current division rule,}\\ {\text{Current through R}}_{\text{3}}\text{ resistor is}\\ 2\frac{4}{16}=0.5\text{A in upward direction }\mathrm{...}\text{(2)}\\ \text{From (1) and (2)}\\ {\text{Total current through R}}_{\text{3}}\text{ resistor is}\\ 0.5-0.4=0.1A\text{ in upward direction}\text{.}\end{array}$

Conclusion:

Hence, the current through $\text{12Ω}$ resistor using superposition theorem for the given network is $\text{0}\text{.1A in upward direction}$.

To determine

(b)

The current through $\text{12Ω}$ resistor using superposition theorem for the given network after converting both the voltage source to current source.

Answer to Problem 1P

The current through $\text{12Ω}$ resistor using superposition theorem for the given network after converting both the voltage source to current source is $\text{0}\text{.1A in upward direction}$.

Explanation of Solution

Given:

The resistors values are ${\text{R}}_1{\text{=4Ω,R}}_2{\text{=2Ω and R}}_3\text{=12Ω}$.

The voltage sources are ${\text{E}}_{\text{1}}{\text{=16V and E}}_{\text{2}}\text{=-10V}$.

Concept Used:

Elements in the series have the same current.

Elements in the parallels have the same voltage.

Superposition theorem states that in any linear bilateral network having more than one source response in any one of the branches is equal to algebraic sum of the responses caused by individual source while rest of the sources are replaced by their internal impedances.

Short circuit the voltage source and open circuit the current source.

If the resistors are in series, then the value of the equivalent resistance for N series resistors is

${\text{R}}_{\text{eq}}{\text{=R}}_{\text{1}}{\text{+R}}_{\text{2}}\text{+}\mathrm{.........}{\text{+R}}_{\text{N}}$.

If the resistors are in parallel, then the value of the equivalent resistance for N series resistors is

$\frac{1}{{\text{R}}_{\text{eq}}}=\frac{1}{{\text{R}}_{\text{1}}}+\frac{1}{{\text{R}}_{\text{2}}}+\mathrm{.........}\text{+}\frac{1}{{\text{R}}_{\text{N}}}$.

The special case for only two parallel resistors is

${\text{R}}_{\text{eq}}\text{=}\frac{{\text{R}}_1{\text{R}}_2}{{\text{R}}_1+{\text{R}}_2}$.

Current: $\text{I=}\frac{\text{V}}{\text{R}}$

$\begin{array}{l}\text{Where V is the voltage}\text{.}\\ \text{ R is the resistance}\text{.}\end{array}$.

Current division is used to express the current across one of several parallel resistors in terms of current across the combination:

If there are two resistors in parallel then the current across second resistor is

$\begin{array}{l}{\text{I}}_{\text{2}}\text{=I(}\frac{{\text{R}}_{\text{1}}}{{\text{R}}_{\text{1}}{\text{+R}}_{\text{2}}}\text{)}\\ \text{Where I is the source current}\text{.}\\ {\text{ I}}_{\text{2}}{\text{ is the current across resistor R}}_{\text{2}}\text{.}\end{array}$

Calculation:

$\begin{array}{l}\text{Converting voltage source to current source}\text{.}\\ I_1=\frac{E_1}{R_1}=\frac{16}{4}=4A\\ I_2=\frac{E_2}{R_2}=\frac{10}{2}=5A\\ \\ {\text{Firstly open circuit the I}}_{\text{2}}\text{ current source}\text{.}\\ \text{Using current division rule,}\\ {\text{Current through R}}_{\text{3}}\text{ resistor is}\\ 4\frac{\frac{1}{12}}{\frac{1}{12}+\frac{1}{2}+\frac{1}{4}}=0.4A\text{ in downward direction }\mathrm{....}\text{(1)}\\ \\ \\ {\text{Secondly,open circuit the I}}_{\text{1}}\text{ current source}\text{.}\\ \text{Total resitance}\\ R_p=12\left|\right|2\\ R_p=\frac{12(2)}{12+2}\\ R_p=1.71\Omega \\ \\ \text{Using current division rule,}\\ \text{Current through 1}\text{.71Ω resistor is}\\ 5\frac{4}{4+1.71}=3.5A\\ {\text{Current through R}}_{\text{3}}\text{ resistor is}\\ 3.5\frac{12}{12+2}=0.5A\text{ in upward direction }\mathrm{....}\text{(2)}\\ \text{From (1) and (2)}\\ {\text{Total current through R}}_{\text{3}}\text{ resistor is}\\ 0.5-0.4=0.1A\text{ in upward direction}\text{.}\end{array}$

Conclusion:

Hence, the current through $\text{12Ω}$ resistor using superposition theorem for the given network after converting both the voltage source to current source is $\text{0}\text{.1A in upward direction}$.

To determine

(c)

Compare the results of both the part (a) and (b).

Answer to Problem 1P

The results are similar in both the part (a) and (b).

Explanation of Solution

Given:

The resistors values are ${\text{R}}_1{\text{=4Ω,R}}_2{\text{=2Ω and R}}_3\text{=12Ω}$.

The voltage sources are ${\text{E}}_{\text{1}}{\text{=16V and E}}_{\text{2}}\text{=-10V}$.

Concept Used:

Elements in the series have the same current.

Elements in the parallels have the same voltage.

Superposition theorem states that in any linear bilateral network having more than one source response in any one of the branches is equal to algebraic sum of the responses caused by individual source while rest of the sources are replaced by their internal impedances.

Short circuit the voltage source and open circuit the current source.

Calculation:

The results are similar in both the part (a) and (b).

Conclusion:

Hence, the results are similar in both the part (a) and (b).