Engineering Mechanics: Statics, Student Value Edition; Modified Mastering Engineering with Pearson eText -- Standalone Access Card -- for Engineering Mechanics: Statics (14th Edition)
14th Edition
ISBN: 9780134246192
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 8.4, Problem 58P
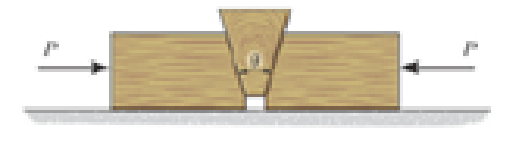
Determine the largest angle θ that will cause the wedge to be self-locking regardless of the magnitude of horizontal force P applied to the blocks. The coefficient of static friction between the wedge and the blocks is, μs = 0.3. Neglect the weight of the wedge.
Expert Solution & Answer
Learn your wayIncludes step-by-step video
schedule06:02
Students have asked these similar questions
Q3: Find the resultant of the force system.
Question 1
A three-blade propeller of a diameter of 2 m has an activity factor AF of 200 and its
ratio of static thrust coefficient to static torque coefficient is 10. The propeller's
integrated lift coefficient is 0.3.
(L=6847 mm, q = 5331 N/mm, M = 1408549 N.mm, and El = 8.6 x 1014 N. mm²)
X
A
ΕΙ
B
L
Y
M
Chapter 8 Solutions
Engineering Mechanics: Statics, Student Value Edition; Modified Mastering Engineering with Pearson eText -- Standalone Access Card -- for Engineering Mechanics: Statics (14th Edition)
Ch. 8.2 - Determine the friction force at the surface of...Ch. 8.2 - Determine M to cause impending motion of the...Ch. 8.2 - Determine the force P to move block B.Ch. 8.2 - Determine the force P needed to cause impending...Ch. 8.2 - Determine the friction developed between the 50-kg...Ch. 8.2 - Determine the minimum force P to prevent the 30-kg...Ch. 8.2 - Determine the maximum force P that can be applied...Ch. 8.2 - If the coefficient of static friction at contact...Ch. 8.2 - Determine the maximum force P that can be applied...Ch. 8.2 - Prob. 6FP
Ch. 8.2 - Blocks A, B, and C have weights of 50 N, 25 N, and...Ch. 8.2 - If the coefficient of static friction at all...Ch. 8.2 - Using the coefficients of static friction...Ch. 8.2 - Determine the maximum force P the connection can...Ch. 8.2 - The tractor exerts a towing force T=400 lb....Ch. 8.2 - Prob. 3PCh. 8.2 - The winch on the truck is used to hoist the...Ch. 8.2 - The automobile has a mass of 2 Mg and center of...Ch. 8.2 - The automobile has a mass of 2 Mg and canter of...Ch. 8.2 - The block brake consists of a pin-connected lever...Ch. 8.2 - The block brake consists of a pin-connected lever...Ch. 8.2 - Prob. 9PCh. 8.2 - Prob. 10PCh. 8.2 - Determine the maximum weight W the man can lift...Ch. 8.2 - The block brake is used to stop the wheel from...Ch. 8.2 - If a torque of M=300 Nm is applied to the...Ch. 8.2 - The car has a mass of 1.6 Mg and center of mass at...Ch. 8.2 - Prob. 15PCh. 8.2 - The 180-Ib man climbs up the ladder and stops at...Ch. 8.2 - The 180-Ib man climbs up the ladder and stops at...Ch. 8.2 - The spool of wire having a weight of 300 Ib rests...Ch. 8.2 - Prob. 19PCh. 8.2 - The ring has a mass of 0.5 kg and is resting on...Ch. 8.2 - A man attempts to support a stack of books...Ch. 8.2 - The tongs are used to lift the 150-kg crate, whose...Ch. 8.2 - The beam is supported by a pin at A and a roller...Ch. 8.2 - The uniform thin pole has a weight of 30 Ib and a...Ch. 8.2 - The uniform pole has a weight of 30 Ib and a...Ch. 8.2 - The block brake is used to stop the wheel from...Ch. 8.2 - Solve Prob. 8-26 if the couple moment M0 is...Ch. 8.2 - A worker walks up the sloped roof that is defined...Ch. 8.2 - Prob. 29PCh. 8.2 - Two blocks A and B have a weight of 10 Ib and 6...Ch. 8.2 - Two blocks A and B have a weight of 10 Ib and 6...Ch. 8.2 - Determine the smallest force P that must be...Ch. 8.2 - The man having a weight of 200 Ib pushes...Ch. 8.2 - The uniform hoop of weight W is subjected to the...Ch. 8.2 - Prob. 35PCh. 8.2 - Determine the minimum force P needed to push the...Ch. 8.2 - Prob. 37PCh. 8.2 - The coefficient of static friction between the...Ch. 8.2 - Determine the smallest coefficient of static...Ch. 8.2 - Prob. 40PCh. 8.2 - If the coefficient of static friction at A and B...Ch. 8.2 - The 100-kg disk rests on a surface for which, B =...Ch. 8.2 - Investigate whether the equilibrium can be...Ch. 8.2 - Prob. 44PCh. 8.2 - The beam AB has a negligible mass and thickness...Ch. 8.2 - It is supported at one end by a pin and at the...Ch. 8.2 - Crates A and B weigh 200 Ib and 150 Ib,...Ch. 8.2 - Two blocks A and B, each having a mass of 5 kg,...Ch. 8.2 - The uniform crate has a mass of 150 kg. If the...Ch. 8.2 - The uniform crate has a mass of 150 kg. If the...Ch. 8.2 - Beam AB has a negligible mass and thickness, and...Ch. 8.2 - Beam AB has a negligible mass and thickness, and...Ch. 8.2 - Determine the smallest couple moment that can be...Ch. 8.2 - Determine the greatest angle so that the ladder...Ch. 8.2 - The wheel weights 20 lb and rests on a surface for...Ch. 8.2 - Prob. 56PCh. 8.2 - The man has a weight of 200 lb, and the...Ch. 8.2 - Prob. 1CPCh. 8.2 - Prob. 4CPCh. 8.2 - Explain how to find the maximum force this man can...Ch. 8.4 - Determine the largest angle that will cause the...Ch. 8.4 - If the beam AD is loaded as shown, determine the...Ch. 8.4 - The wedge is used to level the member. Determine...Ch. 8.4 - Prob. 61PCh. 8.4 - If P=250 N, determine the required minimum...Ch. 8.4 - Determine the minimum applied force P required to...Ch. 8.4 - If the coefficient of static friction between all...Ch. 8.4 - Determine the smallest force P needed to lift the...Ch. 8.4 - Prob. 66PCh. 8.4 - If the clamping force at G is 900 N, determine the...Ch. 8.4 - If a horizontal force of F = 50 N is applied...Ch. 8.4 - Prob. 69PCh. 8.4 - If the force F is removed from the handle of the...Ch. 8.4 - Prob. 71PCh. 8.4 - If the clamping force on the boards is 600 lb,...Ch. 8.4 - Prob. 73PCh. 8.4 - The square-threaded bolt is used to join two...Ch. 8.4 - The shaft has a square-threaded screw with a lead...Ch. 8.4 - If couple forces of F=35 N are applied to the...Ch. 8.4 - Prob. 77PCh. 8.4 - The device is used to pull the battery cable...Ch. 8.4 - Determine the clamping force on the board A if the...Ch. 8.4 - If the required clamping force on the board A is...Ch. 8.4 - If a horizontal force of P = 100 N is applied...Ch. 8.4 - Determine the horizontal force P that must be...Ch. 8.5 - A cylinder having a mass of 250 kg is to be...Ch. 8.5 - A cylinder having a mass of 250 kg is to be...Ch. 8.5 - A 180-lb farmer tries to restrain the cow from...Ch. 8.5 - The 100-lb boy at A is suspended from the cable...Ch. 8.5 - The 100-lb boy at A is suspended from the cable...Ch. 8.5 - Prob. 88PCh. 8.5 - A cable is attached to the 20-kg plate B, passes...Ch. 8.5 - Prob. 90PCh. 8.5 - Prob. 91PCh. 8.5 - Determine the force P that must be applied to the...Ch. 8.5 - Prob. 93PCh. 8.5 - Determine the weight of the cylinder if the...Ch. 8.5 - If slipping does not occur at the wall, determine...Ch. 8.5 - The coefficient of static friction between the...Ch. 8.5 - Prob. 97PCh. 8.5 - Show that the frictional relationship between the...Ch. 8.5 - The wheel is subjected to a torque of M = 50 N m...Ch. 8.5 - Using the coefficients of static friction...Ch. 8.5 - If the coefficient of static friction between the...Ch. 8.5 - Idler pulley A, and motor pulley B. If the motor...Ch. 8.5 - Using the coefficient of static friction...Ch. 8.5 - Determine the smallest counterclockwise twist or...Ch. 8.5 - Determine the largest angles so that the cord...Ch. 8.5 - Determine the smallest stretch of the spring...Ch. 8.8 - If the coefficient of static is, s = 0.3,...Ch. 8.8 - Prob. 108PCh. 8.8 - Prob. 109PCh. 8.8 - Prob. 110PCh. 8.8 - Prob. 111PCh. 8.8 - Prob. 113PCh. 8.8 - Prob. 114PCh. 8.8 - Prob. 115PCh. 8.8 - Prob. 116PCh. 8.8 - Prob. 117PCh. 8.8 - If the coefficient of static friction is. k....Ch. 8.8 - If the coefficient of static friction between the...Ch. 8.8 - If the coefficient of kinetic friction between the...Ch. 8.8 - if the force P is applied horizontally to the...Ch. 8.8 - Prob. 122PCh. 8.8 - Prob. 123PCh. 8.8 - Prob. 124PCh. 8.8 - Prob. 125PCh. 8.8 - The bell crank fits loosely into a 0.5-in-diameter...Ch. 8.8 - Prob. 127PCh. 8.8 - The vehicle has a weight of 2600 lb and center of...Ch. 8.8 - The tractor has a weight of 16 000 lb and the...Ch. 8.8 - Prob. 130PCh. 8.8 - Prob. 131PCh. 8.8 - The 1.4-Mg machine is to be moved over a level...Ch. 8.8 - Prob. 1RPCh. 8.8 - The uniform 60-kg crate C rests uniformly on a...Ch. 8.8 - A 35-kg disk rests on an inclined surface for...Ch. 8.8 - The cam is subjected to a couple moment of 5N m....Ch. 8.8 - The three stone blocks have weights of, WA =...Ch. 8.8 - Prob. 6RPCh. 8.8 - Prob. 7RPCh. 8.8 - Prob. 8RP
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
Multiple Stock Sales Use the method that you wrote for Programming Challenge 10 (Stock Profit) in a program tha...
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
Revise the definition of the method writeOutput in Listing 5.3, using the keyword this. Do not change the meani...
Java: An Introduction to Problem Solving and Programming (8th Edition)
The two general categories of software are ________ and ________.
Starting Out with C++ from Control Structures to Objects (9th Edition)
In Exercises 53 through 56, determine the output produced by the lines of code where Courier New is the font se...
Introduction To Programming Using Visual Basic (11th Edition)
How is the window manager related to the operating system?
Computer Science: An Overview (13th Edition) (What's New in Computer Science)
Determine the slope and deflection of end A of the cantilevered beam. E = 200 GPa and I = 65.0(106) mm4. F122
Mechanics of Materials (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Calculate the maximum shear stress Tmax at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places. Select one: ○ 1.2681.818 O 2. 25745.455 O 3. 17163.636 O 4. 10727.273 ○ 5.5363.636arrow_forwardIf L-719.01 mm, = 7839.63 N/m³, the normal stress σ caused by self-weight at the location of the maximum normal stress in the bar can be calculated as (Please select the correct value of σ given in Pa and rounded to three decimal places.) Select one: ○ 1. 1409.193 2. 845.516 O 3. 11273.545 ○ 4.8455.159 ○ 5.4509.418 6. 2818.386 7.5636.772arrow_forwardTo calculate the rotation at Point B, a suitable virtual structure needs to be created. Which equation in the following choices most accurately represents the functional relationship between the bending moment, Mv2 ( Units: N.mm), of the virtual structure and the spatial coordinate x (Units: mm) if the applied unit virtual moment is clockwise? Select one: O 1. Mv2 1.000 O 2. Mv2=x+1.000 O 3. Mv2=x+0.000 4. Mv2 = -x-1.000 O 5. Mv2 -1.000 6. Mv2=-x+0.000arrow_forward
- The vertical deflection at Point B can be calculated as ( The following choices are provided in units of mm and rounded to three decimal places ; the downward deflection is negative and upward deflection is positive. ) Select one: 1. 1703.065 2. -1703.065 3. -2043.679 4.1362.452 5. -1362.452 6. 2043.679arrow_forwardThe second moments of area about z-axis, /z, and the second moments of area about y-axis, ly, can be calculated as Select one: O 1. I = Iz ○ 2. Ly ○ 3. ○ 4. ○ 5. = = Iz = *D' 64 I₁ = D, Iz Ly Ly = 32 *D' = = 3 Iz = *D' 32 = *D' O 6. Iy=D, Ly = D², Iz = 32 O 7. Ly = Iz D = 64 32arrow_forward[If L=3508 mm, W-9189 N, E=80 GPa, Determine the deflection at the free end of the beam.] Step -2 Which equation in the following choices most accurately represents the functional relationship between the value of the slope O (Units: Radian) at half length (x = L/2) of the beam and the second moment of area about z-axis, Izz (Units: mm²), of the cross section? (Please note that " X = L/2" is the same as "X = L ÷ 2" .) Select one: O 1.0 448787.925/Izz O 2.0 279167.292/Izz O 3.0 38871.395/Izz O 4.0 114847.304/Izz O 5.0 176688.160/Izz O 6.0 609574.150/Izz O 7.0 70675.264/Izzarrow_forward
- Use the principle of virtual work to determine the vertical deflection and rotation at tip (Point B) of the cantilever shown below. (L=6847 mm, q = 5331 N/mm, M = 1408549 N.mm, and El = 8.6 x 1014 N. mm²) q Y M X A ΕΙ B L Step -1 Let the coordinates defined with origin located at B and x-axis pointing to the Left and Y-axis pointing upward. The bending moment, M (Units: N.mm), in the beam as a function of spatial coordinate x(Units: mm) can be most accurately described by Select one: 1. M=1126839.200 +2132.400*x*x 2. M=-1408549.000 - 3198.600*x*x 3. M=-1408549.000-2665.500*x*x 4. M=-1408549.000-2132.400*x*x 5. M= -1408549.000+2665.500*x*x 6. M= 1408549.000 + 2665.500*x*x 7. M= 1408549.000-2665.500*x*xarrow_forwardCalculate the principal stress σ at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places Select one: O 1.5363.64 O 2. 12872.727 3.9118.182 4. 10727.273 5. 16090.909 6. 2681.818arrow_forwardQuestion2 The mission profile for a jet driven aircraft consists of the following segments: engine start and warm-up, taxi, take-off, climb to the cruise altitude of 35000 ft, descend to 10000 ft, one hour loiter at this altitude at 60% of the cruise speed, flight at loiter speed and altitude to an alternate airport (100 nm), descend to landing approach condition followed by the final landing, taxi and shutdown. The cruise Mach number is 0.8. No provisions are made for the reserved fuel or any trapped oil and fuel. The aircraft carries 200 people (including pilots and the cabin crew) at 175 lb each and 90 lb baggage each. This aircraft has a wing area of 2000 ft² L/D at cruise L/D at 10000ft flight Table Q2 20 16 0.43 lb/hr/lb 0.50 lb/hr/lb C: Specific Fuel Consumption at cruise: C: Specific Fuel Consumption at 10000 ft flight: Weight ratios Engine Start and warm-up Taxi Take-off Climb Descent Landing, taxi and shutdown 0.992 0.996 0.996 0.996 0.992 0.992 Question 2 continues on the…arrow_forward
- Calculate the principal stress σ1_at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places. Select one: O 1.25745.455 O 2. 32181.818 3. 21454.545 4. 17163.636 5. 12872.727arrow_forwardCalculate the Von-Mises effective stress at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places Select one: O 1.27870.272 O2. 18580.181 3. 11148.109 O 4. 14864.145 O 5.22296.218arrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Figure Q2 a Figure Q2 b 45°arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Mechanical Design (Machine Design) Clutches, Brakes and Flywheels Intro (S20 ME470 Class 15); Author: Professor Ted Diehl;https://www.youtube.com/watch?v=eMvbePrsT34;License: Standard Youtube License