Engineering Mechanics: Statics Plus Mastering Engineering with Pearson eText -- Access Card Package (14th Edition) (Hibbeler, The Engineering Mechanics: Statics & Dynamics Series, 14th Edition)
14th Edition
ISBN: 9780134160689
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 8.4, Problem 58P
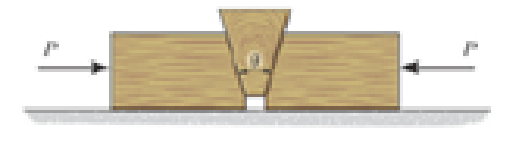
Determine the largest angle θ that will cause the wedge to be self-locking regardless of the magnitude of horizontal force P applied to the blocks. The coefficient of static friction between the wedge and the blocks is, μs = 0.3. Neglect the weight of the wedge.
Expert Solution & Answer
Learn your wayIncludes step-by-step video
schedule06:02
Students have asked these similar questions
4. An operating parameter often used by power plant engineers is the heat rate. The heat rate is
defined as,
HR
Qbioler
Wnet
where Qbioler is the heat transfer rate (Btu/h) to the water in the boiler due to the combustion of a
fuel and Wnet is the net power (kW) delivered by the plant. In comparison, the thermal efficiency
of the power plant is defined as,
nth
Wnet
Qbioler
where the numerator and denominator have the same units. Consider a power plant that is
delivering 1000 MW of power while utilizing a heat transfer rate of 3570 MW at the boiler.
Determine the heat rate and thermal efficiency of this power plant.
The shaft shown in the sketch is subjected to tensile
torsional and bending loads Determine the principal
stresses at the location of stress concentration
✓
D=45MR
F=3MM
1000-M
1000N
チ
d=30mm
500N
150 мм
MM-
120 MA-
calculate moment of inertia of this tapered beam structure
Chapter 8 Solutions
Engineering Mechanics: Statics Plus Mastering Engineering with Pearson eText -- Access Card Package (14th Edition) (Hibbeler, The Engineering Mechanics: Statics & Dynamics Series, 14th Edition)
Ch. 8.2 - Determine the friction force at the surface of...Ch. 8.2 - Determine M to cause impending motion of the...Ch. 8.2 - Determine the force P to move block B.Ch. 8.2 - Determine the force P needed to cause impending...Ch. 8.2 - Determine the friction developed between the 50-kg...Ch. 8.2 - Determine the minimum force P to prevent the 30-kg...Ch. 8.2 - Determine the maximum force P that can be applied...Ch. 8.2 - If the coefficient of static friction at contact...Ch. 8.2 - Determine the maximum force P that can be applied...Ch. 8.2 - Prob. 6FP
Ch. 8.2 - Blocks A, B, and C have weights of 50 N, 25 N, and...Ch. 8.2 - If the coefficient of static friction at all...Ch. 8.2 - Using the coefficients of static friction...Ch. 8.2 - Determine the maximum force P the connection can...Ch. 8.2 - The tractor exerts a towing force T=400 lb....Ch. 8.2 - Prob. 3PCh. 8.2 - The winch on the truck is used to hoist the...Ch. 8.2 - The automobile has a mass of 2 Mg and center of...Ch. 8.2 - The automobile has a mass of 2 Mg and canter of...Ch. 8.2 - The block brake consists of a pin-connected lever...Ch. 8.2 - The block brake consists of a pin-connected lever...Ch. 8.2 - Prob. 9PCh. 8.2 - Prob. 10PCh. 8.2 - Determine the maximum weight W the man can lift...Ch. 8.2 - The block brake is used to stop the wheel from...Ch. 8.2 - If a torque of M=300 Nm is applied to the...Ch. 8.2 - The car has a mass of 1.6 Mg and center of mass at...Ch. 8.2 - Prob. 15PCh. 8.2 - The 180-Ib man climbs up the ladder and stops at...Ch. 8.2 - The 180-Ib man climbs up the ladder and stops at...Ch. 8.2 - The spool of wire having a weight of 300 Ib rests...Ch. 8.2 - Prob. 19PCh. 8.2 - The ring has a mass of 0.5 kg and is resting on...Ch. 8.2 - A man attempts to support a stack of books...Ch. 8.2 - The tongs are used to lift the 150-kg crate, whose...Ch. 8.2 - The beam is supported by a pin at A and a roller...Ch. 8.2 - The uniform thin pole has a weight of 30 Ib and a...Ch. 8.2 - The uniform pole has a weight of 30 Ib and a...Ch. 8.2 - The block brake is used to stop the wheel from...Ch. 8.2 - Solve Prob. 8-26 if the couple moment M0 is...Ch. 8.2 - A worker walks up the sloped roof that is defined...Ch. 8.2 - Prob. 29PCh. 8.2 - Two blocks A and B have a weight of 10 Ib and 6...Ch. 8.2 - Two blocks A and B have a weight of 10 Ib and 6...Ch. 8.2 - Determine the smallest force P that must be...Ch. 8.2 - The man having a weight of 200 Ib pushes...Ch. 8.2 - The uniform hoop of weight W is subjected to the...Ch. 8.2 - Prob. 35PCh. 8.2 - Determine the minimum force P needed to push the...Ch. 8.2 - Prob. 37PCh. 8.2 - The coefficient of static friction between the...Ch. 8.2 - Determine the smallest coefficient of static...Ch. 8.2 - Prob. 40PCh. 8.2 - If the coefficient of static friction at A and B...Ch. 8.2 - The 100-kg disk rests on a surface for which, B =...Ch. 8.2 - Investigate whether the equilibrium can be...Ch. 8.2 - Prob. 44PCh. 8.2 - The beam AB has a negligible mass and thickness...Ch. 8.2 - It is supported at one end by a pin and at the...Ch. 8.2 - Crates A and B weigh 200 Ib and 150 Ib,...Ch. 8.2 - Two blocks A and B, each having a mass of 5 kg,...Ch. 8.2 - The uniform crate has a mass of 150 kg. If the...Ch. 8.2 - The uniform crate has a mass of 150 kg. If the...Ch. 8.2 - Beam AB has a negligible mass and thickness, and...Ch. 8.2 - Beam AB has a negligible mass and thickness, and...Ch. 8.2 - Determine the smallest couple moment that can be...Ch. 8.2 - Determine the greatest angle so that the ladder...Ch. 8.2 - The wheel weights 20 lb and rests on a surface for...Ch. 8.2 - Prob. 56PCh. 8.2 - The man has a weight of 200 lb, and the...Ch. 8.2 - Prob. 1CPCh. 8.2 - Prob. 4CPCh. 8.2 - Explain how to find the maximum force this man can...Ch. 8.4 - Determine the largest angle that will cause the...Ch. 8.4 - If the beam AD is loaded as shown, determine the...Ch. 8.4 - The wedge is used to level the member. Determine...Ch. 8.4 - Prob. 61PCh. 8.4 - If P=250 N, determine the required minimum...Ch. 8.4 - Determine the minimum applied force P required to...Ch. 8.4 - If the coefficient of static friction between all...Ch. 8.4 - Determine the smallest force P needed to lift the...Ch. 8.4 - Prob. 66PCh. 8.4 - If the clamping force at G is 900 N, determine the...Ch. 8.4 - If a horizontal force of F = 50 N is applied...Ch. 8.4 - Prob. 69PCh. 8.4 - If the force F is removed from the handle of the...Ch. 8.4 - Prob. 71PCh. 8.4 - If the clamping force on the boards is 600 lb,...Ch. 8.4 - Prob. 73PCh. 8.4 - The square-threaded bolt is used to join two...Ch. 8.4 - The shaft has a square-threaded screw with a lead...Ch. 8.4 - If couple forces of F=35 N are applied to the...Ch. 8.4 - Prob. 77PCh. 8.4 - The device is used to pull the battery cable...Ch. 8.4 - Determine the clamping force on the board A if the...Ch. 8.4 - If the required clamping force on the board A is...Ch. 8.4 - If a horizontal force of P = 100 N is applied...Ch. 8.4 - Determine the horizontal force P that must be...Ch. 8.5 - A cylinder having a mass of 250 kg is to be...Ch. 8.5 - A cylinder having a mass of 250 kg is to be...Ch. 8.5 - A 180-lb farmer tries to restrain the cow from...Ch. 8.5 - The 100-lb boy at A is suspended from the cable...Ch. 8.5 - The 100-lb boy at A is suspended from the cable...Ch. 8.5 - Prob. 88PCh. 8.5 - A cable is attached to the 20-kg plate B, passes...Ch. 8.5 - Prob. 90PCh. 8.5 - Prob. 91PCh. 8.5 - Determine the force P that must be applied to the...Ch. 8.5 - Prob. 93PCh. 8.5 - Determine the weight of the cylinder if the...Ch. 8.5 - If slipping does not occur at the wall, determine...Ch. 8.5 - The coefficient of static friction between the...Ch. 8.5 - Prob. 97PCh. 8.5 - Show that the frictional relationship between the...Ch. 8.5 - The wheel is subjected to a torque of M = 50 N m...Ch. 8.5 - Using the coefficients of static friction...Ch. 8.5 - If the coefficient of static friction between the...Ch. 8.5 - Idler pulley A, and motor pulley B. If the motor...Ch. 8.5 - Using the coefficient of static friction...Ch. 8.5 - Determine the smallest counterclockwise twist or...Ch. 8.5 - Determine the largest angles so that the cord...Ch. 8.5 - Determine the smallest stretch of the spring...Ch. 8.8 - If the coefficient of static is, s = 0.3,...Ch. 8.8 - Prob. 108PCh. 8.8 - Prob. 109PCh. 8.8 - Prob. 110PCh. 8.8 - Prob. 111PCh. 8.8 - Prob. 113PCh. 8.8 - Prob. 114PCh. 8.8 - Prob. 115PCh. 8.8 - Prob. 116PCh. 8.8 - Prob. 117PCh. 8.8 - If the coefficient of static friction is. k....Ch. 8.8 - If the coefficient of static friction between the...Ch. 8.8 - If the coefficient of kinetic friction between the...Ch. 8.8 - if the force P is applied horizontally to the...Ch. 8.8 - Prob. 122PCh. 8.8 - Prob. 123PCh. 8.8 - Prob. 124PCh. 8.8 - Prob. 125PCh. 8.8 - The bell crank fits loosely into a 0.5-in-diameter...Ch. 8.8 - Prob. 127PCh. 8.8 - The vehicle has a weight of 2600 lb and center of...Ch. 8.8 - The tractor has a weight of 16 000 lb and the...Ch. 8.8 - Prob. 130PCh. 8.8 - Prob. 131PCh. 8.8 - The 1.4-Mg machine is to be moved over a level...Ch. 8.8 - Prob. 1RPCh. 8.8 - The uniform 60-kg crate C rests uniformly on a...Ch. 8.8 - A 35-kg disk rests on an inclined surface for...Ch. 8.8 - The cam is subjected to a couple moment of 5N m....Ch. 8.8 - The three stone blocks have weights of, WA =...Ch. 8.8 - Prob. 6RPCh. 8.8 - Prob. 7RPCh. 8.8 - Prob. 8RP
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
Multiple Stock Sales Use the method that you wrote for Programming Challenge 10 (Stock Profit) in a program tha...
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
Revise the definition of the method writeOutput in Listing 5.3, using the keyword this. Do not change the meani...
Java: An Introduction to Problem Solving and Programming (8th Edition)
The two general categories of software are ________ and ________.
Starting Out with C++ from Control Structures to Objects (9th Edition)
In Exercises 53 through 56, determine the output produced by the lines of code where Courier New is the font se...
Introduction To Programming Using Visual Basic (11th Edition)
How is the window manager related to the operating system?
Computer Science: An Overview (13th Edition) (What's New in Computer Science)
Determine the slope and deflection of end A of the cantilevered beam. E = 200 GPa and I = 65.0(106) mm4. F122
Mechanics of Materials (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The system shown below is in statics equilibrium. Cable OB lies in the xy plane and makes a 30° angle with the positive x-axis. Cable OA lies along the negative y-axis. If the weight of the load being supported is 100 lb, determine the magnitude of the forces in all four cables: OA, OB, OC, and OD.arrow_forwardThis is a mechanics/statics problem involving finding internal reactions, V(x) and M(x). Please refer to image for details. I'm not sure about where to take cuts and how to formulate the equations as a function of x. For my support Reactions I got Ay = 1008.33 lb, By = 1416.67 lb and Cy = 175 lb. and for the first cut V(x) = 1008.33 -250(x) and M(x) = 1008.33x - 125x^2. I'm struggling with the equations for the 2nd and 3rd cut.arrow_forwardAs shown in the figure below, a ring is used to suspend a load and is supported by Cable OA and Spring OB. Given that the tension in Cable OA is 400 N, what is the weight of the load being supported? Assume the system is in static equilibrium.arrow_forward
- 4. (a) State the conditions that must be met to ensure dynamic balance is achieved for long rotors. (b) A rotor carries three out-of-balance discs in planes A, B and C as shown in Figure 4. The out-of- balance mass x radius products of the rotor discs are tabulated in Table 4. The shaft is to be dynamically balanced by adding balancing masses in planes P and Q, spaced along the shaft at a distance da = 800 mm. Determine the magnitude mara and angular position of the balancing mass x radius product that must be added to plane Q. MBB Ов θε mdc Мага End View on Plane P P MBB MATA dA dB dc do Figure 4 moc Table 4 MATA = 0.6 kg mm 6A = 0° d₁ = 200 mm mers = 0.2 kg mm 6g = 45° dB = 400 mm mcrc = 0.4 kg mm Bc=240° dc = 600 mm Ans. (b) = 110.5°, moro = 0.2 kg mmarrow_forwardNeed help in adding demensioning am am so confusedarrow_forwardComplete the following activity. Save as .pdf and upload to the assignment to the dropbox. 口 Use the general dimensioning symbols to correctly specify the following requirements on the drawing above.arrow_forward
- please solve and show workarrow_forwardWater is boiling in a 25 cm diameter aluminum pan (k=237 W/mK) at 95 degrees C. Heat is transferred steadily to the boiling water in the pan through its .5 cm thick flat bottom at a rate of 800 W. if the inner surface temp of the bottom of the pan is 108 degrees C determine the boiling heat transfer coefficent on the inner surface of the pan and the outer surface temp of the bottom of the pan.arrow_forwardplease solve and show workarrow_forward
- please solve and show workarrow_forwardA thin plastic membrane separates hydrogen from air. The molar concentrations of hydrogen in the membrane at the innner and outer surfaces are determined to be 0.045 and 0.002 kmol/m^3 respectiveley. The binary diffusion coefficent of hydrogen in plastic at the operation temp is 5.3*10^-10 m^2/s. Determine the mass flow rate of hydrogen by diffusion through the membrane under steady conditions if the thickeness of the membrane is 2mm and 0.5 mm.arrow_forwardCalculate the vertical cross section moment of inertia for Orientations 1 and 2. State which number is the higher moment of inertia using equation 1. Given: b1=1 in, h1=1.5 in, b2=1.5 in, h2=1 in, t=0.0625 in. Then calculate the maximum deflection for a point load of 8 lb on the free end of the beam using equation 2. Given: E=10.1*10^6 psi. 1. ((bh^3)/12) - (((b-2t)(h-2t)^3))/12) 2. S = (PL^3)/(3EI)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Mechanical Design (Machine Design) Clutches, Brakes and Flywheels Intro (S20 ME470 Class 15); Author: Professor Ted Diehl;https://www.youtube.com/watch?v=eMvbePrsT34;License: Standard Youtube License